Домашнее задание

Институт радиоэлектроники и информационных технологий

Кафедра Автоматики

РАЗРАБОТКА МОДЕЛИ УПРАВЛЯЕМОГО ПРОЦЕССА

(УРОВЕНЬ ТОПЛИВА В ПОПЛАВКОВОЙ КАМЕРЕ КАРБЮРАТОРА)

И КАЧЕСТВЕННЫЙ АНАЛИЗ МОДЕЛИ

Вариант № 70

Индивидуальное домашнее задание

по дисциплине «основы теории сигналов»

Выполнил:

студент группы Р-200101 Катаев Я. В.

дата _____________ подпись _____________

Проверил:

преподаватель Кумков С. И.

Екатеринбург 2012

Содержание

Кафедра Автоматики 1

РАЗРАБОТКА МОДЕЛИ УПРАВЛЯЕМОГО ПРОЦЕССА 1

(УРОВЕНЬ ТОПЛИВА В ПОПЛАВКОВОЙ КАМЕРЕ КАРБЮРАТОРА) 1

И КАЧЕСТВЕННЫЙ АНАЛИЗ МОДЕЛИ 1

Вариант № 70 1

Екатеринбург 2012 1

1. Задание 3

2. Постановка задачи, расчетные формулы 4

3. Структура моделирующей программы 8

4. Результаты моделирования 11

5. Выводы 14

Литература 15

1. Задание 3

2. Постановка задачи, расчетные формулы 4

3. Структура моделирующей программы 7

4. Результаты моделирования 9

5. Выводы 11

Литература 12

1. Задание

Уровень топлива в поплавковой камере карбюратора описывается дифференциальным уравнением:

(1)

(2)

где H — уровень топлива, мм;

k — эффективность управления, мм/с;

U — управление, безразмерный параметр;

A — коэффициент обратной связи, , 1/мм.

В начальный момент, , камера пуста — уровень топлива .

Разработать алгоритмы расчета фазовой траектории управляемого процесса (изменения уровня топлива).

2. Постановка задачи, расчетные формулы

При ближайшем рассмотрении задача сводится к решению простейших дифференциальных уравнений — получение явной зависимости функции — уровня топлива от аргумента — времени.

Решим дифференциальное уравнение на каждом промежутке для наглядности на рис. 1 изображена зависимость H’ = f(H) (фазовая плоскость).

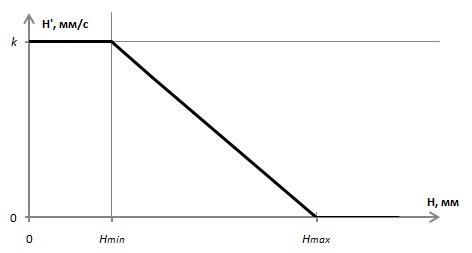
Рис.1. Фазовая плоскость

1. На промежутке (или при ) H(t) — обычная линейная функция:

. (3)

2. На следующем промежутке (или при ) H(t) — экспоненциальная функция:

. (4)

Видно, что

. (5)

Это значит, что при заданных начальных условиях H(t) будет ассимтотично стремиться к , но никогда не достигнет этого уровня и не превысит его, поэтому третий промежуток с практической точки зрения нас не интересует. Однако, по закону, если , то H(t)=const.

При численном моделировании процесса (наполнения поплавковой камеры) можно использовать решения, полученные аналитически: например, если нам нужно заполнить таблицу зависимости H от t, то мы просто возьмем формулу (3), если , или формулу (4), если , и подставим в них значение t. С другой стороны, можно использовать численные методы решения дифференциальных уравнений, например метод Эйлера:

,

,

,

отсюда:

. (6)

Минус числовых методов решения заключается в том, что при расчетах возникает некоторая погрешность, однако у него есть и преимущества: поплавковая камера карбюратора в нашей задаче только наполняется, это значительно упрощает решение, но, если мы захотим модифицировать модель и ввести процесс выхода топлива из поплавковой камеры, описываемый функцией времени, то аналитическое решение может и не получиться, тогда нужно будет использовать только численные методы решения. В своем алгоритме я буду использовать именно метод Эйлера.

Для наглядности нужно не просто выводить численный материал, полученный в результате работы программы, а построить график. Тут же возникает проблема: какие интервалы переменой и значения функции должен охватывать график? Понятно, что значение функции H(t) меняется от 0 до (из начальных условий), но что делать с аргументом? Время t меняется от 0 до некоторого . Если мы возьмем слишком маленьким, то график процесса будет похож на график, изображенный на рис. 2, а если слишком большим — то на график, изображенный на рис. 3. Нужно взять такое, при котором будет достаточно большим, например

Рис.2. График для малого

Рис.3. График для большого

, (7)

где  — некоторый коэффициент, назовем его коэффициентом полноты,   1,  < 1, безразмерный.

Из формул (4) и (7) находим :

. (8)

Найти значение важно так же и из-за того, что оно поможет найти значение T (см. формулу(6)). Допустим, что для построения графика выделено полотно 600 на 800 пикселей. Тогда, грубо говоря (на самом деле величина самого графика будет чуть меньше — из-за запасов на оси и рамку), мы создадим массив a[ ], состоящий из N=800 (800 — ширина полотна) элементов, заполним его значениями H(t) для с шагом времени T и построим график по этим значениям. Значение шага T может быть найдено с помощью формулы

. (9)

Для проверки точности выполненных расчетов, мы сравним a[N-1] и , которое вычислим с помощью формулы (4).

Исходный числовой материал необходимый для численного моделирования решаемой задачи и их ограничения:

 — уровень топлива, после которого наполняемость камеры описывается нелинейной функцией;

 — максимальный уровень топлива;

k, k > 0 — коэффициент управления;

,  — коэффициент наполненности;

N — количество элементов в массиве, должно быть достаточно большим (от 100 элементов).

3. Структура моделирующей программы

На рисунке 4 изображена блок-схема алгоритма. 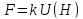— вспомогательная функция.

Рис.4. Блок-схема

В программе ввод числового материала может производиться либо пользователем либо в тестовом режиме они могут задаваться случайно. Ниже представлен код программы, в которой количество элементов в массиве N и коэффициент α заданы изначально и равны соответственно 200 и 0,9999; остальные задаются случайным целым числом: не превышает 50 мм, не больше , чем на 50 мм, k не более 30 мм/с. Примечание: ниже представлен только код, который имеет непосредственное отношение к расчету фазовой траектории процесса, т. е. это не полный код программы.

Значимый код тестовой программы:

static void Main()

{

double Hmin, Hmax, k, tmax, T, F, ras, alpha;

int pix;

Random a = new Random();

pix = 200;

alpha = 0.9999;

Hmin = a.Next(50);

Hmax = Hmin + a.Next(49) + 1;

k = a.Next(29)+1;

tmax = (Hmin - Hmax) / k * Math.Log((1 - alpha) * Hmax / (Hmax - Hmin)) + Hmin / k;

T = tmax / pix;

double[] mas = new double[pix];

mas[0] = 0;

for (int i = 1; i < pix; i++)

{

if (mas[i - 1] < Hmin) F = k;

else if (mas[i - 1] < Hmax) F = k * (Hmax - mas[i - 1]) / (Hmax - Hmin);

else F = 0;

mas[i] = mas[i - 1] + F * T;

}

ras = Hmax - (Hmax - Hmin)*Math.Exp((Hmin - k * tmax)/(Hmax - Hmin)) - mas[pix - 1];

}

4. Результаты моделирования

Вариант 1 (рис. 5):

.

Погрешность вычисления численным методом составила 0,0009 мм.

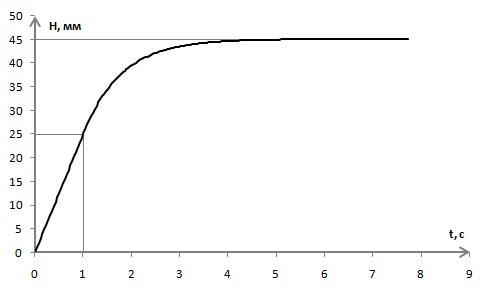
Рис.5. График процесса вариант 1

Вариант 2 (рис. 6):

.

Погрешность вычисления численным методом составила 0,003 мм.

Рис.6. График процесса вариант 2

Вариант 3 (рис. 7):

.

Погрешность вычисления численным методом составила 0,0008 мм.

Рис.7. График процесса вариант 3

На графиках изображена зависимость уровня топлива от времени. Горизонтальные линии соответствуют уровням и , вертикальная — времени . Как видно, графики получились наглядными, хорошо выбран масштаб по оси времени.

5. Выводы

Был разработан алгоритм расчета фазовой траектории управляемого процесса, а именно расчета изменения уровня топлива в поплавковой камере карбюратора во времени. В отчете представлено задание, пояснен смысл задачи, произведена постановка задачи с сопутствующими необходимыми формулами, графиками. Пояснен порядок расчета алгоритма, приведена блок-схема алгоритма и практически значащая часть программы (код). Алгоритм был протестирован, в отчете приведены результаты тестирования и величина погрешностей.

Литература

Павловская Т.А.; С#. Программирование на языке высокого уровня. Учебник для вузов. — СПб.: Питер, 2007. — 432 с.: ил.