Лекция 11, 12

Сортировка

Сортировка — это процесс перегруппировки элементов заданной совокупности с целью расположить их в определённом порядке, т.е. это процесс упорядочения элементов в соответствии с некоторым принципом.

Рассмотрим некоторую совокупность из n элементов:

a₀, a ₁, …, a _n-1

После сортировки элементы располагаются в совокупности в каком-то порядке: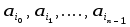

Например, для некоторой функции f(x) элементы перегруппированы так, что

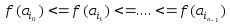
Здесь функция f(x) называется упорядочивающей функцией. Если элементы исходной совокупности с одинаковыми значениями упорядочивающей функции не изменяют своего относительного расположения при перегруппировке, то метод сортировки называют устойчивым.

Примем следующие соглашения:

• элементы совокупности a₀ ,a₁, …a _n-1 — числовые;

• упорядочивающая функция f(x) = x, т.е. f( a_i ) = a_i ;

• элементы в результате сортировки удовлетворяют условию a₀  a ₁  …a _n-1 ;

• сортировка выполняется «на том же месте», т.е. в составе данной совокупности.

Будем рассматривать три группы методов сортировки:

а) сортировка Выбором;

б) сортировка Обменом;

в) сортировка Включением.

В каждой группе рассмотрим

• прямые методы — очевидные, реализующие основную идею, но, может быть, не всегда самые эффективные;

• модификации прямых методов — несколько улучшенные методы с той же основной идеей.

Меру эффективности метода будем оценивать:

• по числу сравнений элементов С(n);

• по числу перемещений элементов M(n);

• по временной сложности метода T(n);

За размер входа в задачах сортировки очевидно выбирается n — количество элементов в совокупности.

А) Сортировка с помощью прямого Выбора: Идея метода:

0 шаг: min { a₀ ,a ₁, …a _n-1 }  a₀

1 шаг: min { a ₁, …a _n-1 }  a₁

_{……………………………………………………….}

(n-2) шаг: min { a_n-2 ,a _n-1 }  a _n-2

Cхема алгоритма:

for (int i=0; i<n-1;i++)

{ <определить место k минимального элемента в совокупности { a_i ,a_i+1 , …a _n-1 }>

< переставить минимальный элемент a_k с a_i >

}

const int n=100;

Пусть: int a[n]; — заданная совокупность.

//сортировка выбором минимального

void selection (int a[], int n)

{for (int i=0;i<n-1;i++)

{int min=a[i] ,m=i;

for(int j=i+1; j<n; j++)

if (a[j]<min) {min=a[j]; m=j;}

a[m]= a[i]; a[i]= min;

} 8 7 6 5 4 3 2 1

} 1 2 6 5 4 3 7 8

1 2 3 5 4 6 7 8

1 2 3 4 5 6 7 8

n-1 +n-3+n-5+…1 =n² / 4

7 6 5 4 3 2 1

1 6 5 4 3 2 7

1 2 5 4 3 6 7

n-1 + n-3+n-5+… 0=(n²-1)/4 1 2 3 4 5 6 7

Характеристики алгоритмасортировки с помощью прямого Выбора:

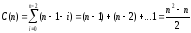
Порядок метода О(n²)

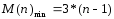
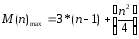
Модификации прямого выбора:

1. Модификация.Идея метода: поиск в просматриваемой совокупности максимального элемента и перестановка его с последним элементом.

0 шаг: max { a₀ ,a ₁, …a _n-1 }  a_n-1

1 шаг: max { a₀, …a _n-2 }  a_n-2

_{……………………………………………………….}

(n-2) шаг: max { a₀,a₁ }  a ₁

Cхема алгоритма:

for (int i=0; i<n;i++)

{<найти место k максимального элемента в совокупности { a₀ ,a₁ , …a _n-1-i }>

< переставить максимальный элемент a_k с a_n-i+1 >

}

Этот алгоритм описать самим

2. Модификация. Идея метода: Соединить в одном просмотре совокупности поиск максимального и поиск минимального элементов, затем переставить минимальный с первым, а максимальный с последним элементом. При этом просматриваемый сегмент сужается с двух сторон.

Cхема алгоритма:

int t=n/2;

for (int i=0; i<t;i++)

{ <найти место m1 максимального и место m минимального элементов в совокупности { a_i ,a_i+1 , …a _n-i-1 }>

< переставить минимальный элемент a_m с a_i >

if m1 = i then m1 := m;

< переставить максимальный элемент a_m1 с a_n-i-1 >

}

//сортировка выбором минимального и максимального

void selection3 (int a [], int n)

{int t=n/2;

for (int i=0; i<t; i++)

{int min = a[i], m = i, max = a[i], m1 = i;

for(int j=i+1 ; j<n-i; j++)

{ if (a[j]<min) { min = a[j]; m = j;}

if (a[j]>max) { max = a[j]; m1 = j;}}

a[m] = a[i]; a[i] = min;

if (m1==i) m1 = m;

a[m1] = a[n-1-i]; a[n-1-i] = max;

}

Б) Сортировка с помощью прямого Обмена: Идея метода

Просматривается каждая пара соседних элементов в совокупности: а_j и а_j+1 для j =0,1,…n-2. Если элементы пары не находятся в нужном отношении, т.е. : а_j > а_j+1 , то они переставляются (меняются местами).

Схема алгоритма:

for (int j=0; j<n-1;j++) if (a[j] > a[j+1] ){ < a[j]  a[j+1] };

Назовём такой просмотр просмотром «Слева направо» ( ) , а просмотр

for (int j=n-2; j>=0;j--) if ( a[j] > a[j+1] ) { < a[j]  a[j+1] }; назовем просмотром Справа налево» ().

Элементы совокупности ассоциируются с пузырьками воздуха в чане с водой: каждый пузырёк со своим весом-значением. Отсюда и название метода пузырьковая сортировка.

Можно отметить, что

• за один просмотр элементы, вообще говоря, не будут упорядочены;

• однако, если во время просмотра не было ни одной перестановки, то совокупность упорядочена; можно сделать вывод, что просмотры необходимо повторять, пока есть перестановки;

• за один просмотр самый тяжелый пузырёк встанет на свое место, поэтому в следующем просмотре его можно не трогать, т.е.в следующих просмотрах уменьшается количество просматриваемых пар;

• за один просмотр самый легкий пузырёк продвинется к своему месту на одну позицию, т.е. если самый легкий пузырек стоял на дне (худший случай), то за (n -1) просмотр он встанет на свое место; отсюда вывод: за (n-1) просмотр совокупность будет упорядочена.

//пузырьковая сортировка

voidbubble(inta[],intn)

{for(inti=0;i<n-1;i++) //n-1 просмотр

for(intj=n-1;j>i;j--) // Просмотры «справа налево» ().

if (a[j-1] > a[j]) {int r = a[j-1] ; a[j-1]= a[j]; a[j]=r;}

}

Характеристики алгоритма сортировки с помощью прямого Обмена:

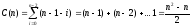
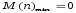
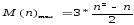
Порядок метода О(n²)

Модификации прямого Обмена:

1. Модификация. Можно выполнять просмотры «Слева направо» ()

//пузырьковая сортировка1

void bubble1 (int a[ ], int n)

{for (int i=n-1;i>0;i--) // n-1 просмотр

for (int j=0; j<i ;j++) // пока j<i, т.к. тяжелый ->на свое место

if (a[j ] > a[j+1]) {int r = a[j] ; a[j]= a[j+1]; a[j+1]=r;}

}

2. Модификация. Запоминание факта перестановки. Недостатком прямого обмена является выполнение (n-1) просмотра даже в случае, если совокупность упорядочится раньше (также в случае заданной упорядоченной совокупности). Удобно организовать проверку, были ли перестановки элементов во время просмотра и, если не было (т.е. совокупность упорядочена), прекратить просмотры.

Схема алгоритма:

i := 0; p := true;

While ( p) //{пока есть перестановки}

{i := i + 1; //{номер просмотра}

p := false;

for (int j=0; j<n-i ; j++) if ( a[j] > a[j+1]) {int R := a[j]; a[j] := a[j+1]; a[j+1] :=R;

p := true //запоминание факта перестановки

}

}

//запоминание факта перестановки

voidbubble2 (inta[ ],intn)

{int i=0;

bool p=true;

while (p)

{i++; p=false; //i-номер просмотра

for(int j=0; j<n-i; j++)

if(a[j]>a[j+1]) { int r = a[j] ; a[j]= a[j+1]; a[j+1]=r;

p=true; //запоминание факта перестановки

} }

3. Модификация. Запоминание места последней перестановки.

a₀ , a₁ , … , a _L-1 , a_L , ……,a_j-1 , a _j , a_j+1 , … ,a_r-1 , a_r , a_r+1 , … ,a _n-1

Если в просмотре «Слева направо» ( ) последняя перестановка была

а_r а_r+1, то элемента_r+1 встал на своё место и следующий просмотр можно выполнять на сегменте {a₀,a₁, … ,a_r-1,a_r }, т.е. возможно более значительное, чем на 1элемент, сужение сегмента просмотра.

Схема алгоритма

r = n-1;

while (r>0) // {Цикл просмотров}

{int t=0;

for (int j=0;j<r;j++)

if (a[j] > a[j+1]) { int v = a[j]; a[j] = a[j+1]; a[j+1] = v;

t=j; // запоминание места перестановки

}

r=t; }

Аналогично для просмотра «Справа налево» (), когда последняя перестановка была а_L  а_L+1 : написать алгоритм самим.

void bubble3 (int a[], int n)

{int r=n-1;

while (r>0) //цикл просмотров

{int t=0;

for(int j=0; j<r; j++)

if(a[j]>a[j+1]) { int z = a[j] ; a[j]= a[j+1]; a[j+1]=z; t=j;}

r=t; }}

4. Модификация. Чередование просмотров «Слева направо» ( ) и «Справа налево» () с запоминанием в каждом просмотре места последней перестановки — так называемая Шейкерная сортировка.

//чередование просмотров с запоминанием мест последних //перестановок

void bubble4 (int a[], int n)

{int L=0, r=n-2, t=L;

do

{//-->

for (int j=L;j<=r;j++)

if(a[j]>a[j+1])

{int v= a[j]; a[j]=a[j+1]; a[j+1]=v; t=j;}

r=t-1;

// -

for(int j=r;j>=L;j--)

if(a[j]>a[j+1])

{ int v= a[j]; a[j]=a[j+1]; a[j+1]=v; t=j;}

L=t+1; //запоминание места перестановки

}

while (L<=r);

}