
- •Вопрос 1. Первообразная и ее общий вид
- •Вопрос 2. Свойства неопределенного интеграла
- •Вопрос 3. Интегрирование заменой переменной и подстановкой в неопределенном интеграле
- •Вопрос 4. Интегрирование по частям неопределенного интеграла
- •Вопрос 5. Необходимое условие интегрируемости функции.
- •Вопрос 6. Суммы Дарбу и их свойства.
- •Вопрос 7. Лемма Дарбу-Римана.
- •Вопрос 8. Критерий интегрируемости
- •Вопрос 9.Свойства интеграла Римана
- •Вопрос 10.Интегрируемость непрерывной функции
- •Вопрос 11. Интегрируемость ограниченной функции с конечным числом точек разрыва.
- •Вопрос 12. Интегрируемость функции, монотонной на отрезке.
- •Вопрос 13. Теоремы о среднем для интеграла.
- •Вопрос 14. Свойства интеграла с переменным верхним пределом интегрирования.
- •Вопрос 15. Формула Ньютона-Лейбница и её обобщение.
- •Вопрос 16. Интегрирование заменой переменной и по частям в определённом интеграле
- •Вопрос 17. Векторные пространство Rm, скалярные произведения, модуль, расстояние.
- •Вопрос 18. Критерии замкнутости в метрическом пространстве.
- •1 Критерий замкнутости
- •2 Критерий замкнутости
- •Вопрос 19. Свойство компактности в метрическом пространстве.
- •Вопрос 20. Компактность m-мерного отрезка.
- •Вопрос 21. Критерий компактности в Rm.
- •Вопрос 22. Критерий Коши и покоординатная сходимость.
- •Вопрос 23. Теорема Больцано-Вейерштрасса
- •Вопрос 24. Предел функции по направлению и предел по совокупности переменных.
- •Вопрос 25. Повторные и двойные пределы.
- •26. Непрерывность сложной функции многих переменных.
- •27. Теорема Коши о промежуточном значении функции.
- •28. Теоремы Вейерштрасса для функций многих переменных.
- •29. Дифференцируемость функции многих переменных, вид нелинейной части.
Вопрос 8. Критерий интегрируемости
А)в терминах s(T),S(T)
Б)I*,I*
Полезным для дальнейшего является понятие колебания функции fна отрезке (𝛼,𝛽):
𝜔 (f,[𝛼,𝛽]) =sup f(x)-inf f(x)=M-m
В частности
𝜔(f,[xk,xk+1])=𝜔k(f)=Mk-mk.
Следовательно,
S(T)-s(T)=
Сформулируем необходимое и достаточное условие интегрируемости функции на отрезке [a,b]
Теорема (Критерий Римана).
Для того чтобы ограниченная функция fбыла интегрируемой на отрезке [a,b],
необходимо и достаточно, чтобы для
любого >0
нашлось такое разбиение Т отрезка [a,b],
при которомS(T)-s(T)<𝜀(или
>0
нашлось такое разбиение Т отрезка [a,b],
при которомS(T)-s(T)<𝜀(или <𝜀)
<𝜀)
Замечание 1
Из этого
условия следует, что интегрируемость
функции fравносильна
тому, что для любого𝜀>0
найдется разбиение отрезка [a,b],
при котором график функцииfможно поместить в «змейку», составленную
из прямоугольников общей площади меньше𝜀(см. рисунок)

Доказательство.
Необходимость. <=
Из определения
интегрируемости функции fна [a,b]
следует, что для любого𝜀>0 найдется𝛿>0
такое, что для всех разбиений Т𝜖 ,
мелкость которых𝜆(Т)<𝛿, и для
всех
,
мелкость которых𝜆(Т)<𝛿, и для
всех к𝜖[xk,xk+1],k=0,…,n-1,
выполняется условие
к𝜖[xk,xk+1],k=0,…,n-1,
выполняется условие
I-𝜀/3< <I+𝜀/3
<I+𝜀/3
Переходя
к supиinfв
этих неравенствах по к𝜖[xk,xk+1],k=0,…,n-1 и
воспользовавшись свойством 1 сумм Дарбу,
получим
к𝜖[xk,xk+1],k=0,…,n-1 и
воспользовавшись свойством 1 сумм Дарбу,
получим
I-𝜀/3 s(T)
s(T)
Отсюда
S(T)-s(T) I+𝜀/3-(I-𝜀/3)=2𝜀/3<𝜀
I+𝜀/3-(I-𝜀/3)=2𝜀/3<𝜀
Достаточность. =>
Пусть 𝜀>0
произвольно и Т𝜖 – такое разбиение отрезка [a,b],
при которомS(T)-s(T)<𝜀.
По свойствамs(T),S(T),I*,I*имеем (см. рисунок)
– такое разбиение отрезка [a,b],
при которомS(T)-s(T)<𝜀.
По свойствамs(T),S(T),I*,I*имеем (см. рисунок)

s(T) I*
I* I*
I* S(T)
S(T)
Отсюда, по условию теоремы,
I*-I* S(T)-s(T)<𝜀
S(T)-s(T)<𝜀
Следовательно, ввиду произвольности 𝜀>0, имеемI*=I*=I.
Докажем
теперь, что функция fинтегрируема на [a,b]
и интеграл от нее равен числуI.
Возьмем произвольное𝜀>0, тогда по лемме Дарбу существует𝛿(𝜀)>0
такое, что для любого разбиения Т𝜖 отрезка [a,b]
мелкостью𝜆(Т)<𝛿(𝜀)
выполняется
отрезка [a,b]
мелкостью𝜆(Т)<𝛿(𝜀)
выполняется
I-𝜀<s(T) S(T)<I+𝜀.(1)
S(T)<I+𝜀.(1)
В силу того,
что для любого
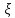 k𝜖[xk,xk+1],k=0,…,n-1,
k𝜖[xk,xk+1],k=0,…,n-1,
s(T) из неравенства (1) имеем
из неравенства (1) имеем
I-𝜀<
Вопрос 9.Свойства интеграла Римана
Пусть функция fинтегрируема на отрезке [a,b]. Тогда она интегрируема на любом отрезке [a1,b1]
 [a,b].
[a,b].Пусть a<c<b. Тогда, если функцияfинтегрируема на отрезках [a,c] и [c,b], она интегрируема на отрезке [a,b] и имеет место равенство

Пусть функции fиgинтегрируемы на отрезке [a,b]. Тогда их суммаf(x)+g(x) также интегрируема на отрезке [a,b] и имеет место равенство

Пусть функция fинтегрируема на отрезке [a,b], аC-константа. Тогда функция Сf(x) интегрируема на отрезке [a,b] и имеет место равенство

Пусть функции fиgопределены на отрезке [a,b], причем функцияfинтегрируема на отрезке [a,b], а функцияgотличается от функцииfв конечном числе точек. Тогда функцияgтоже интегрируема на отрезке [a,b] и имеет место равенство

Если функции fиgинтегрируемы на отрезке [a,b], то их произведениеfgтоже интегрируемо на отрезке [a,b].
Пусть функция fинтегрируема на отрезке [a,b] иf
 0.
Тогда
0.
Тогда

Пусть функция fинтегрируема на отрезке [a,b]. Тогда функция |f| интегрируема на отрезке [a,b] и имеет место неравенство
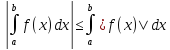
Докажем некоторые из перечисленных свойств.
1)Пусть задано произвольное 𝜀>0.
В силу критерия интегрируемости функцииfна отрезке [a,b]
существует разбиение Т, при которомS(T)-s(T)<𝜀.
Пусть Т` - разбиение отрезка [a,b],
полученное из разбиения Т добавлением
точекa1,b1,
т.е. Т’ =T {a1,b1}
{a1,b1} T.
Пусть теперь Т1-разбиение отрезка
[a1,b1],
образованное точками разбиения Т`,
принадлежащими отрезку[a1,b1]
T.
Пусть теперь Т1-разбиение отрезка
[a1,b1],
образованное точками разбиения Т`,
принадлежащими отрезку[a1,b1] [a,b].
Тогда
[a,b].
Тогда
S(T1)-s(T1)= .
.
Поскольку
T T’,
то по свойствам сумм Дарбу
T’,
то по свойствам сумм Дарбу
s(T) s(T’)
s(T’) S(T’)
S(T’) S(T)
S(T)
и, следовательно,
S(T’)-s(T’) S(T)-s(T),
т.е.
S(T)-s(T),
т.е.

Итак, нашлось разбиение T1отрезка [a1,b1], при котором

Следовательно, функция fинтегрируема на отрезке [a1,b1] по критерию интегрируемости (теорема 9.5.1)
5)Рассмотрим функцию
u(x)=g(x)-f(x),
u(x)=0
на отрезке [a,b],
за исключением конечного числа точек 1,
1, 2,…,
2,…, p.
Возьмем любое𝜀>0,
а𝛿=𝜀/2pM.
ПустьM=max{|u(x1)|,…,|u(xp)|}
иT– разбиение отрезка
[a,b] настолько
мелкое, что каждая из точек
p.
Возьмем любое𝜀>0,
а𝛿=𝜀/2pM.
ПустьM=max{|u(x1)|,…,|u(xp)|}
иT– разбиение отрезка
[a,b] настолько
мелкое, что каждая из точек
 1,
1, 2,…,
2,…, pпринадлежит не более чем двум отрезкам
разбиения Т(либо она лежит внутри –
тогда одному отрезку, либо на границе
– тогда двум отрезкам) и𝜆(Т)<𝛿.
Тогда для функцииu(x)
имеем
pпринадлежит не более чем двум отрезкам
разбиения Т(либо она лежит внутри –
тогда одному отрезку, либо на границе
– тогда двум отрезкам) и𝜆(Т)<𝛿.
Тогда для функцииu(x)
имеем
S(T)-s(T)=
Отсюда, по критерию интегрируемости, функция u(x), а следовательно, и функцияg(x)=f(x)+u(x) интегрируемы на отрезке [a,b]. Из неравенств

Следует
 ,
и поэтому
,
и поэтому

Замечание1.
Если у интегрируемой функции fна отрезке [a,b] изменить значения в конечном числе точек, то она останется интегрируемой, и величина интеграла не изменится.
6)Поскольку
функции fиgинтегрируемы на отрезке [a,b],
то они ограничены на нем. Следовательно,
существуетM>0 такое ,
что дляx𝜖[a,b]
: |f(x)| Mи |g(x)|
Mи |g(x)| M.
Тогда в силу критерия интегрируемости
для любого𝜀>0
найдутся разбиения Т1и Т2,
при которых
M.
Тогда в силу критерия интегрируемости
для любого𝜀>0
найдутся разбиения Т1и Т2,
при которых
Sf(T1)-sf(T1)< ,
Sg(T1)-sg(T1)<
,
Sg(T1)-sg(T1)<
Возьмем
разбиение T=T1 T2.
Поскольку разбиение Т отрезка [a,b]
является измельчением разбиений Т1,Т2,
по свойствам сумм Дарбу для функцийfиgимеет место
T2.
Поскольку разбиение Т отрезка [a,b]
является измельчением разбиений Т1,Т2,
по свойствам сумм Дарбу для функцийfиgимеет место
s(T1) s(T)
s(T) S(T)
S(T) S(T1).
S(T1).
Отсюда
S(T)-s(T) S(T1)-s(T1).
S(T1)-s(T1).
Поэтому
Sf(T1)-sf(T1) Sf(T1)-sf(T1)<
Sf(T1)-sf(T1)<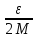
Итак,

Где 𝜔k(f)- колебание функции на [xk,xk+1],

Где 𝜔k(g) колебание функции на [xk,xk+1]
Докажем теперь, что для колебания 𝜔k(fg) функцииf(x)g(x) на отрезке [xk,xk+1] имеет место неравенство
𝜔k(fg) M(𝜔k(f)+𝜔k(g)).
M(𝜔k(f)+𝜔k(g)).
Возьмем
любые
 ,
, ,𝜖[xk,xk+1],
тогда
,𝜖[xk,xk+1],
тогда
f( )g(
)g( )-f(
)-f( )g(
)g( )=f(
)=f( )g(
)g(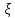 )-f(
)-f( )g(
)g( )+f(
)+f( )g(
)g( )-f(
)-f(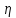 )g(
)g( )=f(
)=f( )[g(
)[g( )-g(
)-g( )]+g(
)]+g( )[f(
)[f( )-f(
)-f( )].
)].
Поэтому
|f( )g(
)g( )-f(
)-f( )g(
)g( )|
)| M|f(
M|f( )-f(
)-f( )|+M|g(
)|+M|g( )-g(
)-g( )|
)|
Следовательно, по свойству 4 сумм Дарбу и свойству точных границ
𝜔k(fg)= f(
f( k)g(
k)g( k)
–
k)
– f(
f( k)g(
k)g( k)=
k)= [f(
[f(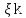 )g(
)g( k)-f(
k)-f( k)g(
k)g(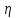 k)]=
k)]=
 |f(
|f( )g(
)g( k)-f(
k)-f( k)g(
k)g( k)|
k)| M[
M[ |f(
|f(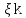 )-f(
)-f( )|+
)|+ |g(
|g( k)-g(
k)-g( k)|]=[снова
по свойству 4]=M[
k)|]=[снова
по свойству 4]=M[ -
- f(
f( )]+M[
)]+M[ -
- g(
g( )]=M(𝜔k(f)+𝜔k(g)).
)]=M(𝜔k(f)+𝜔k(g)).
Поэтому по
построению разбиения T=T1 T2,
имеем
T2,
имеем
 =M(
=M( ∆xk
+
∆xk
+
 )<M(
)<M( )
)
Следовательно, по критерию интегрируемости, произведение функций f(x)g(x) интегрируемо на отрезке [a,b]
Замечание 2
Вообще говоря, интеграл от произведения функций не равен произведению интегралов т.е.

