
- •Вопрос 1. Первообразная и ее общий вид
- •Вопрос 2. Свойства неопределенного интеграла
- •Вопрос 3. Интегрирование заменой переменной и подстановкой в неопределенном интеграле
- •Вопрос 4. Интегрирование по частям неопределенного интеграла
- •Вопрос 5. Необходимое условие интегрируемости функции.
- •Вопрос 6. Суммы Дарбу и их свойства.
- •Вопрос 7. Лемма Дарбу-Римана.
- •Вопрос 8. Критерий интегрируемости
- •Вопрос 9.Свойства интеграла Римана
- •Вопрос 10.Интегрируемость непрерывной функции
- •Вопрос 11. Интегрируемость ограниченной функции с конечным числом точек разрыва.
- •Вопрос 12. Интегрируемость функции, монотонной на отрезке.
- •Вопрос 13. Теоремы о среднем для интеграла.
- •Вопрос 14. Свойства интеграла с переменным верхним пределом интегрирования.
- •Вопрос 15. Формула Ньютона-Лейбница и её обобщение.
- •Вопрос 16. Интегрирование заменой переменной и по частям в определённом интеграле
- •Вопрос 17. Векторные пространство Rm, скалярные произведения, модуль, расстояние.
- •Вопрос 18. Критерии замкнутости в метрическом пространстве.
- •1 Критерий замкнутости
- •2 Критерий замкнутости
- •Вопрос 19. Свойство компактности в метрическом пространстве.
- •Вопрос 20. Компактность m-мерного отрезка.
- •Вопрос 21. Критерий компактности в Rm.
- •Вопрос 22. Критерий Коши и покоординатная сходимость.
- •Вопрос 23. Теорема Больцано-Вейерштрасса
- •Вопрос 24. Предел функции по направлению и предел по совокупности переменных.
- •Вопрос 25. Повторные и двойные пределы.
- •26. Непрерывность сложной функции многих переменных.
- •27. Теорема Коши о промежуточном значении функции.
- •28. Теоремы Вейерштрасса для функций многих переменных.
- •29. Дифференцируемость функции многих переменных, вид нелинейной части.
Вопрос 5. Необходимое условие интегрируемости функции.
Теорема. Необходимое условие интегрируемости
Если fинтегрируема на отрезке [a,b], то она ограничена на этом отрезке
Доказательство
Пусть функция fне ограничена на отрезке [a,b], но интегрируема на нем. Тогда согласно определению интегрируемости, с одной стороны,
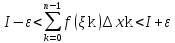
Для какого-то
разбиения Т𝜖 при заданном𝜀>0
и любом выборе
при заданном𝜀>0
и любом выборе k𝜖[xk,xk+1].
С другой стороны (см рисунок) найдется
отрезок разбиения [xk,xk+1]
на котором функцияfне
ограничена и, следовательно, слагаемоеf(
k𝜖[xk,xk+1].
С другой стороны (см рисунок) найдется
отрезок разбиения [xk,xk+1]
на котором функцияfне
ограничена и, следовательно, слагаемоеf(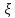 k)∆xk,
а поэтому и вся сумма
k)∆xk,
а поэтому и вся сумма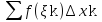 ,
выбором точки
,
выбором точки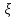 к
могут быть сделаны сколь угодно
большими.
к
могут быть сделаны сколь угодно
большими.
Ограниченность функции есть лишь необходимое условие ее интегрируемости. Достаточно рассмотреть в качестве примера функцию Дирихле
D(x)=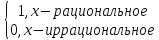
Очевидно,
что эта функция ограничена на любом
отрезке числовой прямой, но не интегрируема
на нем, так как при любом разбиении этого
отрезка при выборе точек
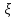 k,k=0…n-1,
рациональными числами интегральная
сумма равна длине отрезка, а при выборе
иррациональными – равна нулю.
k,k=0…n-1,
рациональными числами интегральная
сумма равна длине отрезка, а при выборе
иррациональными – равна нулю.
Вопрос 6. Суммы Дарбу и их свойства.
Введение в рассмотрение сумм Дарбу позволяет существенно упростить проверку интегрируемости функции. Пусть задано произвольное разбиение Tотрезка [a,b] и
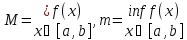
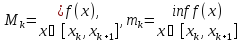
Верхняя сумма Дарбу есть
S(T)=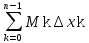
Нижняя сумма Дарбу есть
s(T)=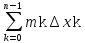
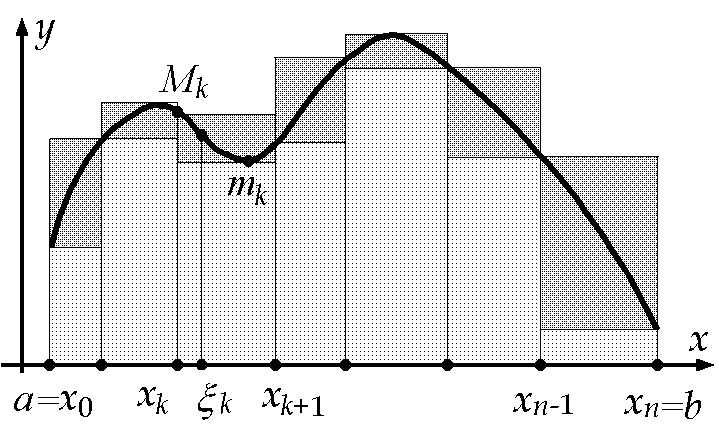
На рисунке заштрихована светлой штриховкой фигура, площадь которой численно равна s(T).
Свойства сумм Дарбу
1)Справедливы следующие соотношения:
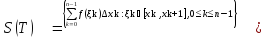
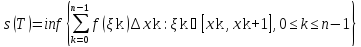
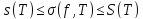
2)Если
все точки разбиения Т отрезка [a,b]
входят в число точек разбиения Т’ того
же отрезка [a,b],
то говорят что разбиение Т’ является
измельчением разбиения Т, и пишут: Т Т’,
то
Т’,
то
S(Т’)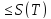 ,s(T)
,s(T)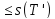
Таким образом, при добавлении к разбиению Т дополнительных точек разбиения верхняя сумма Дарбу может только лишь уменьшится, а нижняя сумма Дарбу – только лишь увеличиться.

Из рисунка видно что при добавлении точки x’ в число точек разбиения Т верхняя сумма Дарбу уменьшится на величину площади незаштрихованного прямоугольника
3)для любых разбиений Т1 и Т2 отрезка [a,b]
m(b-a)=s(T0)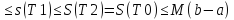
Таким образом, множества чисел s(T1)иS(T2) при любых Т1и Т2расположены так, как показано на РИСУНКЕ (3)
Вопрос 7. Лемма Дарбу-Римана.
Теорема.
Пусть функция fограничена на отрезке [a,b]. Тогда для любого𝜀>0 найдется такое𝛿(𝜀)>0, что для любого разбиения Т отрезка [a,b] с мелкостью разбиения𝜆(Т)<𝛿(𝜀) выполняется
I*-𝜀<s(T)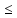 S(T)<I*+𝜀.
S(T)<I*+𝜀.
Доказательство:
Пусть 𝜀>0
произвольно и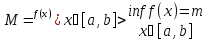
(при М=mутверждение очевидно, так какs(T)=S(T)=I*=I*=M(b-a)).
Из определения
I*и точной верхней
границы множества следует, что существует
такое разбиениеT1𝜖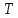 ,
при котором
,
при котором
I*
-
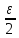 <s(T1).
<s(T1).
Пусть p– количество точек разбиения Т1внутри интервала (a,b).
Зададим число𝛿1(𝜀)=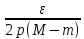 >0
и возьмем любое разбиение Т={x0,x1,…,xn}
отрезка [a,b],
мелкостью которого𝜆(Т)<𝛿1(𝜀).
Построим разбиение Т’=T
>0
и возьмем любое разбиение Т={x0,x1,…,xn}
отрезка [a,b],
мелкостью которого𝜆(Т)<𝛿1(𝜀).
Построим разбиение Т’=T T1.
По второму свойству сумм Дарбу, так какT1
T1.
По второму свойству сумм Дарбу, так какT1 T’
T’
I*
-
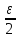 <s(T1)
<s(T1) s(T’).
s(T’).
Предположим, что точка x’ из разбиенияT1попала внутрь отрезка [xk,xk+1] разбиенияT1. Тогда имеют место следующие неравенства:
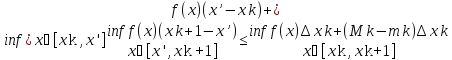
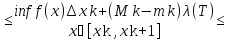

Mk



mk


Поэтому
s(T’) s(T)+p(M-m)𝜆(T)<[по
выбору 𝜆(T)]<
S(T)+p(M-m)𝛿1(𝜀)=s(T)+
s(T)+p(M-m)𝜆(T)<[по
выбору 𝜆(T)]<
S(T)+p(M-m)𝛿1(𝜀)=s(T)+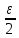
Окончательно имеем
I*-
 <s(T)+
<s(T)+
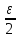
Т.е. I*-𝜀<s(T) для любого разбиения Т мелкостью меньше𝛿1(𝜀). Аналогично для данного𝜀>0 найдется𝛿2(𝜀) такое, что для всех разбиений Т мелкостью меньше𝛿2(T) выполняетсяS(T)<I*+𝜀. Выбирая теперь𝛿(𝜀)=min(𝛿1(𝜀),𝛿2(𝜀)), получим требуемое: для любого Т с мелкостью𝜆(T)<𝛿(𝜀) выполняется
I*-𝜀<s(T)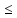 S(T)<I*+𝜀
S(T)<I*+𝜀
Замечание
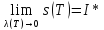
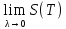 =I*
=I*
