- •Вопрос 1. Первообразная и ее общий вид
- •Вопрос 2. Свойства неопределенного интеграла
- •Вопрос 3. Интегрирование заменой переменной и подстановкой в неопределенном интеграле
- •Вопрос 4. Интегрирование по частям неопределенного интеграла
- •Вопрос 5. Необходимое условие интегрируемости функции.
- •Вопрос 6. Суммы Дарбу и их свойства.
- •Вопрос 7. Лемма Дарбу-Римана.
- •Вопрос 8. Критерий интегрируемости
- •Вопрос 9.Свойства интеграла Римана
- •Вопрос 10.Интегрируемость непрерывной функции
- •Вопрос 11. Интегрируемость ограниченной функции с конечным числом точек разрыва.
- •Вопрос 12. Интегрируемость функции, монотонной на отрезке.
- •Вопрос 13. Теоремы о среднем для интеграла.
- •Вопрос 14. Свойства интеграла с переменным верхним пределом интегрирования.
- •Вопрос 15. Формула Ньютона-Лейбница и её обобщение.
- •Вопрос 16. Интегрирование заменой переменной и по частям в определённом интеграле
- •Вопрос 17. Векторные пространство Rm, скалярные произведения, модуль, расстояние.
- •Вопрос 18. Критерии замкнутости в метрическом пространстве.
- •1 Критерий замкнутости
- •2 Критерий замкнутости
- •Вопрос 19. Свойство компактности в метрическом пространстве.
- •Вопрос 20. Компактность m-мерного отрезка.
- •Вопрос 21. Критерий компактности в Rm.
- •Вопрос 22. Критерий Коши и покоординатная сходимость.
- •Вопрос 23. Теорема Больцано-Вейерштрасса
- •Вопрос 24. Предел функции по направлению и предел по совокупности переменных.
- •Вопрос 25. Повторные и двойные пределы.
- •26. Непрерывность сложной функции многих переменных.
- •27. Теорема Коши о промежуточном значении функции.
- •28. Теоремы Вейерштрасса для функций многих переменных.
- •29. Дифференцируемость функции многих переменных, вид нелинейной части.
Вопрос 1. Первообразная и ее общий вид
Функция F,
определенная на конечном или бесконечном
промежуткеE𝜖 называетсяпервообразной функции,
или первообразной, функцииfна промежуткеE, если она
дифференцируема на нем и имеет место
равенствоF’(x)=f(x)
для каждогоx𝜖E.
называетсяпервообразной функции,
или первообразной, функцииfна промежуткеE, если она
дифференцируема на нем и имеет место
равенствоF’(x)=f(x)
для каждогоx𝜖E.
Теорема
Если F– какая либо первообразная функцииfна промежуткеEто всякая функция вида Ф(х)=F(x)+Cтакже является первообразной для функцииfна промежуткеEи всякая первообразная функцииfпредставима в таком виде.
Доказательство
Пусть Ф и
F– две первообразные для
функцииfна промежуткеE, т.е. Ф’(x)=f(x)
иF’(x)=f(x),x𝜖E. Следовательно,[Ф(х)-F(x)]’=Ф’(x)-F’(x)=0
на промежуткеE. Рассмотрим
функцию (х)=Ф(х)-F(х).
Эта функция имеет производную, всюду
равную нулю. Возьмем любые точки х1,х2𝜖E.
Функция
(х)=Ф(х)-F(х).
Эта функция имеет производную, всюду
равную нулю. Возьмем любые точки х1,х2𝜖E.
Функция удовлетворяет теореме Лагранжа на
отрезке [x1,x2]
(непрерывна на [x1,x2],
дифференцируема на (х1,х2)).Следовательно,
по этой теореме существует
удовлетворяет теореме Лагранжа на
отрезке [x1,x2]
(непрерывна на [x1,x2],
дифференцируема на (х1,х2)).Следовательно,
по этой теореме существует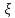 𝜖(х1,х2)
такая, что𝜑(x1)-𝜑(x2)=𝜑’(x)(x1-x2)=0.
Отсюда следует, что𝜑(х)
𝜖(х1,х2)
такая, что𝜑(x1)-𝜑(x2)=𝜑’(x)(x1-x2)=0.
Отсюда следует, что𝜑(х) constнаE.
Следовательно, Ф(х)=F(x)+C.
Итак, все первообразные дляf(x)=2xесть Ф(х)=х2+С.
constнаE.
Следовательно, Ф(х)=F(x)+C.
Итак, все первообразные дляf(x)=2xесть Ф(х)=х2+С.
Пусть
функция fимеет первообразную
на некотором промежуткеE.
Неопределенным интегралом от функцииfна промежуткеEназывается совокупность всех первообразных
функций дляfнаE,
и она обозначается .Поэтому
.Поэтому
 ,
,
Где F– одна из первообразных дляfнаE.
Вопрос 2. Свойства неопределенного интеграла
1)Если функция Fдифференцируема на промежуткеE, то

Доказательство:

Fпервообразная дляF’
2)Пусть для функции fсуществует первообразная на промежуткеE, тогда

Доказательство:
 где
F первообразная
на E
где
F первообразная
на E
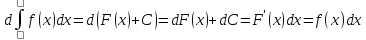
3)Если функции f1иf2 имеют первообразные на промежуткеE, то функцияf1+f2тоже имеет первообразную наE, и имеет место равенство

Доказательство:
Пусть F1 первообразнаяf1на Е,F2 первообразнаяf2на Е
1)F1(x)+F2(x) –первообразнаяf1(x)+f2(x) на Е
Берем
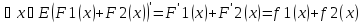
2)Берем
 ;F(x)=F1(x)+C1+F2(x)+C2
;F(x)=F1(x)+C1+F2(x)+C2
F(x)=F1(x)+F2(x)+C
𝜖

Обратное аналогично
4)Пусть fимеет первообразную на Е. Тогда kf(x) имеет
первообразную наEи
kf(x) имеет
первообразную наEи
Доказательство
1)Пусть Fпервообразнаяfна Е, тогдаkF(x) – первообразнаяkf(x) на Е
Берем
 x𝜖E(kF(x))’=kF’(x)=kf(x)
x𝜖E(kF(x))’=kF’(x)=kf(x)
2)Берем

Ф(x)=kF(x)+C=k(F(x)+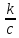 )𝜖
k*
)𝜖
k*
Берем

Ф(x)=k*(F(x)+C)=KF(x)+kc𝜖
Вопрос 3. Интегрирование заменой переменной и подстановкой в неопределенном интеграле
Теорема.Пусть функцииf(u)
иu=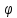 (x)
определены на некоторых промежутках,
что имеет смысл сложная функцияf[
(x)
определены на некоторых промежутках,
что имеет смысл сложная функцияf[ ].
Пусть функцияfимеет
первообразнуюF, а функция
].
Пусть функцияfимеет
первообразнуюF, а функция дифференцируем, тогда функцияf[
дифференцируем, тогда функцияf[ (x)]
(x)]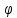 ’(x)
имеет первообразную Ф(х)=F[
’(x)
имеет первообразную Ф(х)=F[ (x)].
(x)].
Доказательство.ФункцииFиfопределены на одном промежутке,
следовательно, имеет смысл сложная
функцияF[ (x)].
По правилу вычисления производной
сложной функции имеем
(x)].
По правилу вычисления производной
сложной функции имеем
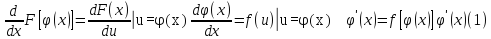
Таким
образом, функция f[ ]
] имеет в качестве одной из своих
первообразных функциюF[
имеет в качестве одной из своих
первообразных функциюF[ ].
].
Замечание. Формула (1) называется еще формулой интегрирования подстановкой, так как учитывая, что
Ф(х)+С=F[ (x)]+C=F[u]
(x)]+C=F[u]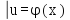 +C=
+C= ,
Ф(х)+С=
,
Ф(х)+С= ,
ей можно придать следующий вид:
,
ей можно придать следующий вид:
 .
.
Равенство
2 понимается так: для вычисления интеграла
 сначала вычисляют
сначала вычисляют ,
а затем подставляют вместо переменной
и функциюu=
,
а затем подставляют вместо переменной
и функциюu= .
.
Вопрос 4. Интегрирование по частям неопределенного интеграла
Если функции u и vдифференцируемы на некотором промежуткеEи существует первообразная дляu’vнаE, то существует первообразная дляuv’ наEи имеет место формула
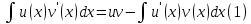
Доказательство.
(u(x)v(x))’=u(x)v’(x)+u’(x)v(x). Следовательно,u(x)v’(x)=(u(x)v(x))’-u’(x)v(x). Первообразная правой части этого равенства существует наE, поэтому существует первообразная наEи для и для левой частиu(x)v’(x).
Формула интегрирования по частям (1) следует из равенства

Замечание. Учитывая равенства du=u’(x)dx,dv=v’(x)dx, формулу интегрирования по частям можно записать в таком виде: