
- •2. Одна из вершин треугольника находится в полюсе , две другие имеют координаты и . Тогда площадь треугольника равна …
- •Площадь треугольника можно вычислить по формуле , где – угол между сторонами и . Тогда .
- •Тема: Прямая на плоскости
- •Тема: Плоскость в пространстве
- •Тема: Кривые второго порядка
- •Тема: Определение линейного пространства
Тема: Полярные координаты
на плоскости
1.
Уравнение прямой линии
![]() в
полярных координатах имеет вид …
в
полярных координатах имеет вид …
Решение:
Перейти
от прямоугольных координат к полярным
можно по формулам
 .
Тогда уравнение прямой примет вид
.
Тогда уравнение прямой примет вид
![]() ,
или
,
или
 .
.
2. Одна из вершин треугольника находится в полюсе , две другие имеют координаты и . Тогда площадь треугольника равна …
Площадь треугольника можно вычислить по формуле , где – угол между сторонами и . Тогда .
Тема:
Полярные координаты на плоскости
В
полярной системе координат дана точка
 .
Тогда расстояние от нее до полярной оси
равно …
.
Тогда расстояние от нее до полярной оси
равно …
|
|
|
|
4 |
|
|
|
|
8 |
|
|
|
|
16 |
|
|
|
|
2 |
Решение:
Расстояние
от точки
![]() до
полярной оси определяется длиной
перпендикуляра, опущенного из нее на
ось. Рассмотрим прямоугольный треугольник
до
полярной оси определяется длиной
перпендикуляра, опущенного из нее на
ось. Рассмотрим прямоугольный треугольник
![]() ,
где
,
где
![]() –
полюс,
–
полюс,
![]() –
основание перпендикуляра. Тогда длина
перпендикуляра
–
основание перпендикуляра. Тогда длина
перпендикуляра ![]() будет
равна:
будет
равна:
![]() .
.
Тема: Полярные
координаты на плоскости
В
полярной системе координат заданы две
точки
 и
и
 .
Тогда расстояние между ними равно …
.
Тогда расстояние между ними равно …
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
Решение:
Точки
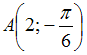 и
и
 лежат
на одной прямой и отстоят от полюса на
расстояния 2 и 7 соответственно.
Следовательно, длина образованного ими
отрезка
лежат
на одной прямой и отстоят от полюса на
расстояния 2 и 7 соответственно.
Следовательно, длина образованного ими
отрезка
![]() .
.
Тема: Полярные
координаты на плоскости
В
полярной системе координат даны две
точки
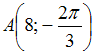 и
и
 .
Тогда полярные координаты середины
отрезка
.
Тогда полярные координаты середины
отрезка
![]() равны …
равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Точки
![]() и
и
![]() в
полярной системе координат лежат на
одной прямой. Длина отрезка
в
полярной системе координат лежат на
одной прямой. Длина отрезка
![]() равна
10. Середина отрезка лежит на луче
равна
10. Середина отрезка лежит на луче
![]() и
удалена от полюса на 3 ед. Следовательно,
полярные координаты середины отрезка
и
удалена от полюса на 3 ед. Следовательно,
полярные координаты середины отрезка
![]() равны
равны
 .
.
Тема: Полярные
координаты на плоскости
Кривая
в полярной системе координат задана
уравнением
![]() .
Тогда ее уравнение в прямоугольной
системе координат имеет вид …
.
Тогда ее уравнение в прямоугольной
системе координат имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Перейдем
в уравнении кривой к декартовым
координатам. Используя формулы взаимосвязи
между полярными и декартовыми системами
координат
![]() ,
,
 ,
получим:
,
получим:
 ,
тогда
,
тогда
 или
или
![]() .
Выделим в этом уравнении полный квадрат
относительно
.
Выделим в этом уравнении полный квадрат
относительно
![]() :
:
![]() .
Тогда
.
Тогда
![]() .
А это уравнение окружности с центром в
точке
.
А это уравнение окружности с центром в
точке
![]() и
радиусом
и
радиусом
![]() .
.
Тема: Прямая на плоскости
1. Уравнение прямой,
проходящей через точку
![]() с
угловым коэффициентом
с
угловым коэффициентом
![]() ,
имеет вид:
,
имеет вид:
![]() .
.
2. Прямая, проходящая
через две данные точки
![]() и
и
![]() ,
задается уравнением вида:
,
задается уравнением вида:
 .
.
Тема: Прямая на
плоскости
Прямая
линия проходит через точки
![]() и
и
![]() .
Тогда она пересекает ось
.
Тогда она пересекает ось
![]() в
точке …
в
точке …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Прямая,
проходящая через две данные точки
![]() и
и
![]() ,
задается уравнением вида:
,
задается уравнением вида:
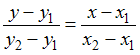 .
Тогда
.
Тогда
![]() ,
или
,
или
![]() .
Точка, лежащая на оси
.
Точка, лежащая на оси
![]() ,
имеет координаты
,
имеет координаты
![]() .
Тогда
.
Тогда
![]() и
и
![]() .
.
Тема:
Прямая на плоскости
Площадь
треугольника, образованного пересечением
прямой
![]() с
осями координат, равна …
с
осями координат, равна …
|
|
|
|
54 |
|
|
|
|
36 |
|
|
|
|
12 |
|
|
|
|
9 |
Решение:
Приведем
уравнение прямой
![]() к
уравнению прямой «в отрезках»:
к
уравнению прямой «в отрезках»:
![]() или
или
![]() .
Уравнение прямой «в отрезках», отсекающей
на координатных осях
.
Уравнение прямой «в отрезках», отсекающей
на координатных осях
![]() и
и
![]() отрезки
длиной
отрезки
длиной
![]() и
и
![]() соответственно,
имеет вид:
соответственно,
имеет вид:
![]() .
Следовательно, треугольник, образованный
прямой
.
Следовательно, треугольник, образованный
прямой
![]() и
осями координат – прямоугольный, с
вершинами
и
осями координат – прямоугольный, с
вершинами
![]() ,
,
![]() ,
,
![]() и
гипотенузой
и
гипотенузой
![]() .
Площадь треугольника
.
Площадь треугольника
![]() будет
равна:
будет
равна:
![]() .
.
Тема:
Прямая на плоскости
Прямые
![]() и
и
![]() пересекаются
в точке, лежащей на оси абсцисс. Тогда
эта точка имеет координаты …
пересекаются
в точке, лежащей на оси абсцисс. Тогда
эта точка имеет координаты …
|
|
|
|
|
Тема:
Прямая на плоскости
Прямые
![]() и
и
![]() …
…
|
|
|
|
перпендикулярны |
|
|
|
|
пересекаются под острым углом |
|
|
|
|
совпадают |
|
|
|
|
параллельны |
Тема:
Прямая на плоскости
Уравнение
геометрического места точек, равноудаленных
от двух данных точек
![]() и
и
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|





































