
- •Оглавление
- •§ 2. Существование и единственность интерполяционного многочлена
- •§ 3. Интерполяционный многочлен Лагранжа
- •§ 4. Погрешность интерполяционного многочлена Лагранжа
- •§ 5. Минимизация погрешности интерполяционного многочлена Лагранжа. Многочлен Чебышева
- •§ 6. Схема Эйткена
- •§ 7. Численное дифференцирование
- •§ 8. Погрешность простейших формул численного дифференцирования
- •§ 9. Разделенные разности. Многочлен Ньютона.
- •§ 10. Интерполяция с кратными узлами
- •§ 11. Кубическая сплайн-интерполяция
- •ГлаваIii. Численное интегрирование
- •§ 1. Простейшие квадратурные формулы. Составные формулы
- •§ 2. Метод неопределенных коэффициентов
- •§ 3. Формулы Ньютона-Котеса
- •§ 4. Формулы Гаусса
- •§ 5. Погрешность квадратурных формул. Правило Рунге.
- •ГлаваIv. Численные методы алгебры
- •§1. Системы линейных уравнений: метод простых итераций, метод Зейделя
- •§2. Метод наискорейшего спуска
- •§ 3. Обратная интерполяция для решения нелинейных уравнений
- •§ 4. Системы нелинейных уравнений: метод простых итераций
- •§ 5. Системы нелинейных уравнений: метод Ньютона
- •§ 6. Методы спуска
- •Глава V. Дифференциальные уравнения и системы
- •§ 1. Задача Коши для обыкновенных дифференциальных уравнений: применение формулы Тейлора
- •§ 2. Метод Эйлера. Методы Рунге-Кутта
- •§ 3. Конечно-разностные методы
- •§ 4. Уравнения второго порядка
§2. Метод наискорейшего спуска
Итерационные
методы решения СЛУ сводятся к поиску
вектора
![]() ,
минимизирующего функцию
,
минимизирующего функцию![]() .
.
Воспользуемся теорией ФНП из мат.анализа:
![]() –вектор, в
направлении которого скорость возрастания
–вектор, в
направлении которого скорость возрастания
![]() наибольшая.
наибольшая.
![]() ,
где
,
где
![]() – частная производная по переменнойl.
– частная производная по переменнойl.
Получаем рекуррентную формулу:
![]() (6),
(6),
где
![]() – некоторый параметр, определяемый из
условия:
– некоторый параметр, определяемый из
условия:
![]() .
.
Особый случай.
Пусть A – симметричная и положительно определенная матрица.
Пусть
![]() .
.
Точка минимума
такой функции является решением уравнения
![]() .
.
Доказывается подстановкой и по определению – пропускаем.
Тогда
 .
.
![]() .
.
![]()
![]()
Пусть
![]() .
.
![]() ,
где
,
где
![]() – параметр, определяемый из условия:
– параметр, определяемый из условия:
![]() .
.
Выведем формулу
для нахождения
![]() .
.
Рассмотрим
![]()
![]()
![]()
![]()
(т.к. A
– симметричная, то
![]()
Т.о.
![]() – квадратная функция с положительным
коэффициентом при
– квадратная функция с положительным
коэффициентом при![]() .
.
(т.к. A
– положительно определенная, то
![]() для любого
для любого![]() )
)
![]() в точке
минимума.
в точке
минимума.
![]()
![]() –значение, при
котором
–значение, при
котором
![]() .
.
§ 3. Обратная интерполяция для решения нелинейных уравнений
Задача: Дано: f(x) = 0
Найти: x0, такой, что f(x0)=0.
Пусть точное решение xT [a,b] и f(x) обратима на [a,b], т.е. существует обратная функция g(x) = f–1(x): g(f(x))=x.
Тогда g(0)=g(f(xT))=xT.
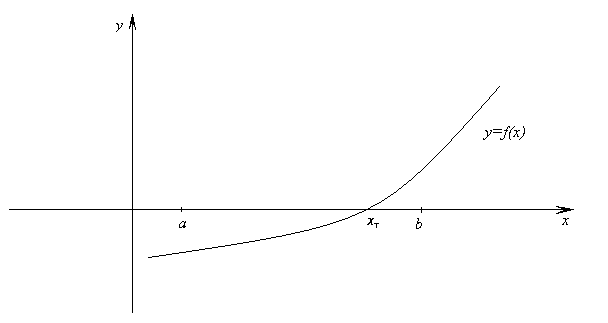

Алгоритм:
1) Выбрать [a,b]: f(x) обратима (монотонна).
2) Выбрать узлы x0, ..., xn [a,b].
Вычислить значения f(x) в узлах: f(x0), ..., f(xn).
3) Для g(x): f(x0), ..., f(xn) — узлы
x0, ..., xn — значения в узлах.
Найти интерполяционный многочлен Ln(x) g(x).
4) Ln(0) g(0) = xT — приближенное значение корня уравнения.
§ 4. Системы нелинейных уравнений: метод простых итераций
Задача: Дано:
![]() (7),
(7),
где
 – столбец неизвестных,
– столбец неизвестных, – столбец, состоящий из скалярных
функций отn
переменных.
– столбец, состоящий из скалярных
функций отn
переменных.
Метод простых итераций:
1) Преобразовать
уравнение (7) в уравнение вида
![]() (8) ;
(8) ;
2) Составить
рекуррентную формулу:
![]() (9);
(9);
3) Выбрать любое
начальное приближение
![]() .
По формуле (9) найти
.
По формуле (9) найти![]() ,
,![]() ,
…,
,
…,![]() ;
;
4) Если норма
разности
![]() уменьшается, то метод сходится, и
последнее найденное приближение
уменьшается, то метод сходится, и
последнее найденное приближение![]() приблизительно равно решению системы
(7).
приблизительно равно решению системы
(7).
Опр. Метрическое пространство H — множество, на котором задана функция метрики (расстояния) (a,b), удовлетворяющая условиям:
1) (a,b) 0, и (a,b) = 0 a = b;
2) (a,b) = (b,a);
3) (a,b) + (b,c) (a,c).
В нашем случае H
= n,
![]() .
.
Опр. Отображением в метрическом пространстве называется функция
g : H H.
Опр. Отображение называется сжимающим, если существует число q:
0 ≤ q < 1, такое, что для любых x1, x2 H выполняется
(g(x1),g(x2)) ≤ q(x1, x2).
Теорема.
Если отображение
![]() является сжимающим, то уравнение
является сжимающим, то уравнение![]() имеет единственное решение
имеет единственное решение![]() и
и![]() .
.
Док-во:
1. Поскольку
![]() является сжимающим, то
является сжимающим, то
![]()
![]() (обозначили
(обозначили
![]() ).
).
Тогда для l > k выполняется
![]()
![]()
![]()
Т.о. при l
,
k
выполняется
![]() ,
следовательно последовательность
,
следовательно последовательность
![]() ,
,![]() ,
…,
,
…,![]() ,…
сходится к предельному значению
,…
сходится к предельному значению![]() .
.
2.
![]()
![]() .
.
Это неравенство
верно для любого k,
т.е.
![]() меньше сколь угодно маленького
положительного числа, т.е.
меньше сколь угодно маленького
положительного числа, т.е.![]() .
.
Следовательно,
![]() — точное решение уравнения (8).
— точное решение уравнения (8).
3. Предположим, что
уравнение (8) имеет два точных решения
![]() и
и![]() .
.
![]() .
.
![]()
![]() .
.
Теорема доказана.
Частный случай. Пусть n = 1, т.е. система состоит из одного уравнения
f(x) = 0 с одной неизвестной x.
Уравнению равносильно x = g(x). Решение xT — точка пересечения графиков функций y = x и y = g(x).

x1 = g(x0), x2 = g(x1), …

На этом рисунке метод простых итераций сходится.
На следующем — нет.

Аналогом метода
Зейделя является способ, когда координаты
нового приближения
 вычисляются по очереди из одного
уравнения системы:
вычисляются по очереди из одного
уравнения системы:
 .
.
