Лабораторная работа №4

Министерство образования и науки Российской Федерации

ФГАОУ ВПО «Уральский федеральный университет

имени первого Президента России Б.Н.Ельцина»

Кафедра «Информационные технологии и автоматизации проектирования»

Оценка

ЛАБОРАТОРНАЯ РАБОТА №4. Процедуры и функции

По дисциплине: «Информационные технологии»

Студент: Мишкин Кирилл Олегович

Группа: ММ-121102

Преподаватель: Склярова Наталья Сергеевна

г. Екатеринбург

2012

Постановка задачи

Основная задача.

Написать программу для численного интегрирования функций и на любом отрезке с заданной точностью. Отладить программу при помощи интегрирования функций, для которых известны аналитические выражения первообразных (т.е. можно рассчитать точные значения интегралов и сравнить их с полученными приближенными). При расчете и выводе приближенных значений на экран ограничиться шестью десятичными знаками, для точных выводить 12 знаков.

Дополнительные задачи.

1. Организовать меню из четырех пунктов (интегрирование функций , , , ). Написать процедуру PrintIntegr, в которую будут передаваться две функции: интегрируемая функция и ее первообразная. Процедура должна выдавать на экран приближенное и точное значения интеграла. При выборе последних двух функций, для которых первообразная неизвестна, передавать в процедуру вместо первообразной значение NIL. Процедура должна корректно обрабатывать этот случай и не выдавать в этом случае точного значения интеграла.

2. Добавить в меню пункт «Выход» и организовать в основной программе внешний цикл WHILE, как в третьей лабораторной работе. Организовать в процедуре PrintIntegr цикл REPEAT, который будет выполняться, пока на запрос «Продолжить вычисление (Y/N) ?» не будет введено «N».

Математическая модель

Интеграл приближенно заменяем суммой:

,

что эквивалентно замене площади под кривой набором отдельных прямоугольников, как показано на следующем рисунке.

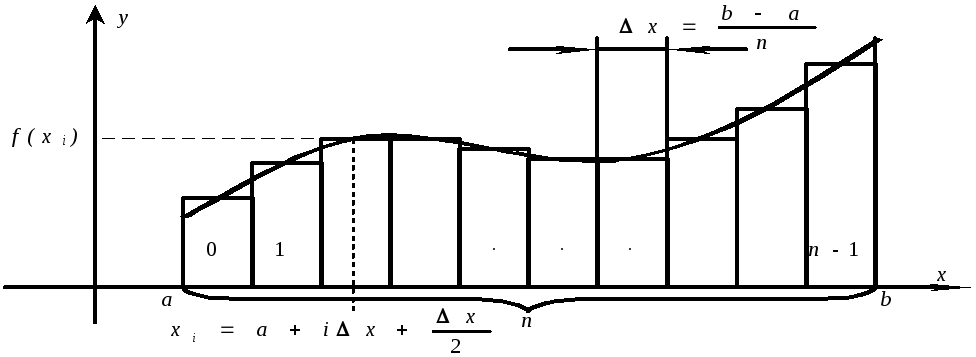
Для тестирования программы будем применять две функции с известными первообразными:

, , , .

Точное значение интеграла будем рассчитывать по формуле Ньютона-Лейбница: .

Описание алгоритма

Алгоритм Lab4.

А. Начать исполнение.

1. Присвоить переменной Loop значение "истина".

2. Пока Loop имеет значение "истина", повторять:

А. Вывести на экран меню: "1 – Интегрирование функции 2 – Интегрирование функции 3 – Интегрирование функции 4 – Интегрирование функции 5 – Выход".

Б. Вывести сообщение "Выберите пункт меню".

В. Ввести n.

Г. Исследовать n:

1. Если n=1, то вызвать подпрограмму PrintIntegr для функции f1 с первообразной G1.

2. Если n=2, то вызвать подпрограмму PrintIntegr для функции f2 с первообразной G2.

3. Если n=3, то вызвать подпрограмму PrintIntegr для функции f3 без первообразной.

4. Если n=4, то вызвать подпрограмму PrintIntegr для функции f4 без первообразной.

5. Если n=5, то присвоить переменной Loop значение "ложь".

3. Конец цикла.

Б. Закончить исполнение.

Текст программы

program Lab4;

{$APPTYPE CONSOLE}

uses

SysUtils;

type

Func=function (x:Real):Real;

function Sum(f:Func;a,b:Real;n:Integer):Real;

var

dx:Real;

i:Integer;

begin

dx:=(b-a)/n;

Result:=0;

for i:=0 to n-1 do

Result:=Result+dx*f(a+i*dx+dx/2);

end;

function Integr(f:Func;a,b,MaxError:Real):Real;

var

n:Integer;

Prev:Real;

begin

n:=8;

Result:=Sum(f,a,b,n);

repeat

Prev:=Result;

n:=n*2;

Result:=Sum(f,a,b,n);

until Abs(Result-Prev)<MaxError;

end;

procedure PrintIntegr(f,G:Func);

var

a,b:Real;

ch:Char;

begin

repeat

Write('vvedite otrezok inegrirovaniya: ');

ReadLn(a,b);

Writeln('Priblizhennoe znachenie integrala'),

Integr(f,a,b,1e-6):1:6,'+-',1e-6:1:6);

if @G<>nil then

Writeln('Tochnoe znachenie integrala '),

G(b)-G(a):1:10);

Write('Continued? (Y/N) ? ');

Readln(ch);

until UpCase(ch)='N';

end;

function f1(x:Real):Real;

begin f1:=x*sin(x) end;

function G1(x:Real):Real;

begin G1:=sin(x)-x*cos(x) end;

function f2(x:Real):Real;

begin f2:=sqr(cos(x)) end;

function G2(x:Real):Real;

begin G2:=x/2+sin(2*x)/4 end;

function f3(x:Real):Real;

begin f3:=sin(x)/x end;

function f4(x:Real):Real;

begin f4:=exp(sqr(x)) end;

var

n:Integer;

Loop:Boolean;

begin

Loop:=True;

while Loop do

begin

Writeln('1. integral of function x*sin(x)');

Writeln('2. integral of function sqr(cos(x))');

Writeln('3. integral of function sin(x)/x');

Writeln('4. integral of function exp(sqr(x))');

Writeln('5. exit');

Write('viberite punkt menu: ');

Readln(n);

Writeln;

case n of

1:PrintIntegr(f1,G1);

2:PrintIntegr(f2,G2);

3:PrintIntegr(f3,nil);

4:PrintIntegr(f4,nil);

5:Loop:=False;

end;

Writeln;

end;

readln;

end.

end.

Тест

Функция	a	b	Приближенное значение интеграла	Точное значение интеграла
x sin x	0	1	0.3011680.000001	0.3011686789
x sin x	0	2	1.7415910.000001	1.7415910999
x sin x	2	3	1.3695070.000001	1.3695063979
x sin x	0	3	3.1110980.000001	3.1110974979
cos2 x	0	1	0.7273250.000001	0.7273243567
cos2 x	0	2	0.8107990.000001	0.8107993762
cos2 x	2	3	0.6193470.000001	0.6193467493
cos2 x	0	3	1.4301460.000001	1.4301461255
sin x/x	1	2	0.6593300.000001	–
sin x/x	2	3	0.2432390.000001	–
sin x/x	1	3	0.9025700.000001	–
ex2	0	1	1.4626520.000001	–
ex2	1	2	14.9899760.000001	–
ex2	0	2	16.4526280.000001	–