Уральский государственный технический университет -упи-

Физико-технический факультет

Кафедра теоретической физики и прикладной математики

СБОРНИК ЗАДАЧ И УПРАЖНЕНИЙ

ПО КУРСУ

РАДИОЭЛЕКТРОНИКА

Методическое пособие

для студентов второго года обучения

ЕКАТЕРИНБУРГ

2012

Настоящее руководство предназначено для практических занятий по курсу « Радиоэлектроника» для студентов второго курса кафедры теоретической физики и прикладной математики. В него включены задачи и упражнения по следующим разделам курса: элементы общей теории сигналов, методы математического моделирования сигнала и системы, основы теории линейных электрических цепей, теория линейных четырехполюсников, спектральный и временной подходы в теории линейных систем.

Литература 5 назв.

Составитель Л.Н.Новиков, профессор, к.ф.-м. н.

1. преобразования пассивных схем

Задача 1. 1

Определитьдвухполюсника при разомкнутом и замкнутом ключе К.

Задача 1. 2

Найти входные сопротивления ,,в приведенной на рисунке схеме.

Задача 1. 3

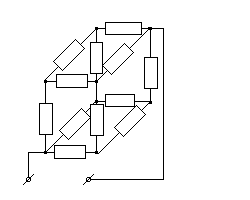
Найти входное сопротивление куба, собранного из сопротивлений 1 Ом, относительно клемм, выведенных от его главной диагонали.

Задача 1. 4

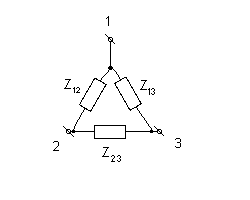
Выразить элементы R₁ ,R₂,R₃через элементыR₁₂,R₂₃,R₁₃так, чтобы обе схемы были эквивалентными (преобразование «треугольника» в «звезду»).

2.Основы общей теории сигналов

Задача 2. 1

Составьте динамическое представление сигнала, изображенного на рисунке.

Задача 2. 2

Составьте динамическое представление сигнала, изображенного на рисунке.

Задача 2. 3

Ключ К замыкается в момент времени мсек. ЭДС источника изменяется по закону. Составить динамическое представление сигналана выходе схемы и построить график его зависимости от времени.

Задача 2. 4

Найти спектры следующих периодических колебаний:

а) пилообразное колебание

,

где n- любое целое число, аT=const- период колебаний.

2. периодическая последовательность униполярных треугольных импульсов:

при,

где n- любое целое число, аT=const- период колебаний ;

с) периодическая последовательность униполярных прямоугольных импульсов:

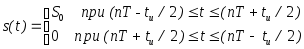
где n- любое целое число,T=const- период колебания и- длительность импульса.

4. периодическая последовательность косинусоидальных импульсов:

.

Задача 2. 5

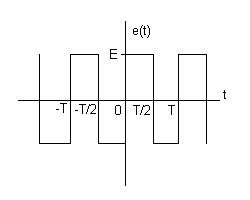
Разложить сигнал, заданный периодической функцией, изображенной на рисунке, в ряд Фурье.

Задача 2. 6

Вычислить спектральную плотность одиночного прямоугольного импульса, изображенного на рисунке.

Задача 2. 7

Найти спектральную плотность одиночного пилообразного импульса при, при других значенияхсигнал равен нулю.

Задача 2. 8

Найти спектральную плотность экспоненциального видеоимпульса: , если длительность импульсаопределяют из условия, то есть.

Задача 2. 9

Найти спектральную плотность сигнала, имеющего форму - функции:.

Задача 2. 10

Найти спектральную плотность радиоимпульса : .

Задача 2. 11

Найти спектральную плотность гармонического колебания .

Задача 2. 12

Найти спектральную плотность произведения сигналов , если спектральные плотности сигналов равны соответственнои.

Задача 2. 13

Найти спектральную плотность радиоимпульса , если соответствующие спектральные плотностиравныи.

3. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ЦЕПЕЙ

Задача 3-1

При измерении с помощью осциллографа напряжения и тока на входе пассивного двухполюсника получены следующие осциллограммы (см. рисунок):

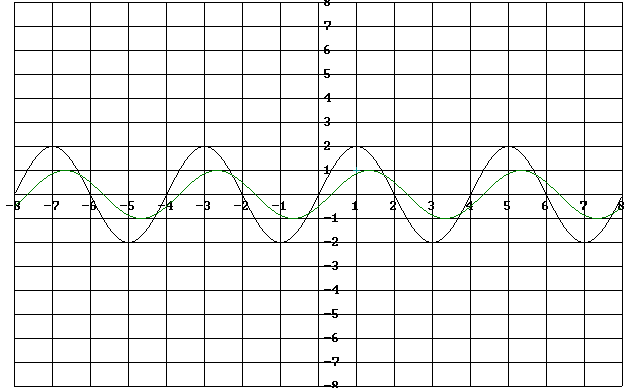
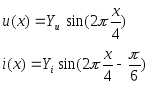
Здесь - отсчет амплитуды напряжения по осциллограмме (в см),- отсчет амплитуды тока по осциллограмме (в см),- отсчет фазы по осциллограмме (в см), причем,, и. Определить, из каких элементов состоит двухполюсник и определить их параметры.

Задача 3-2

Модуль амплитуды напряжения на конденсатореU_c=192 В, модули сопротивлений равны:

R=28 Ом,R₂=50 Ом,|X_c|=96 Ом

Найти амплитуду напряжения U, приложенного к цепи, а также амплитуды токовIиI₂.

Задача 3-3

Каким активным сопротивлениемR₂следует зашунтировать сопротивлениеZ₁=R₁+jX₁, чтобы токI₁отставал от приложенного напряженияUна 90⁰, если известны параметры других элементов схемы?

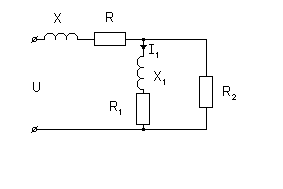
R=5 Ом,R₁=10 Ом,|X|=11 Ом,|X₁|=25 Ом.

Задача 3-4

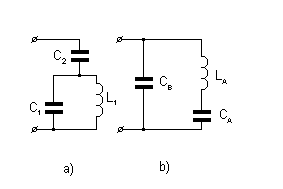
Определить элементы L_A,C_A,C_B черезC₁,C₂,L₁ , если входные сопротивления двухполюсников одинаковы.

Задача 3-5

При каких соотношениях между параметрами элементов контура его входное сопротивление не зависит от частоты?

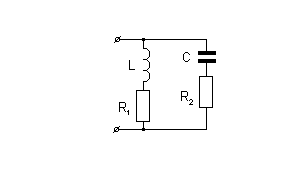
Задача 3-6

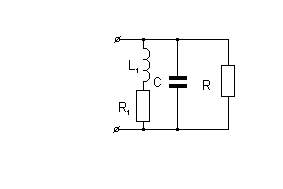
Определить резонансную частоту контура, нагруженного на активное сопротивление R, если на частоте резонанса.

Задача 3-7

Вычислить АЧХ (то есть ) фильтра нижних частот, нагруженного на активное сопротивление.