
- •Модуль 2. Молекулярная физика Лекция 1
- •2.1. Статистический и термодинамический методы описания свойств
- •Макроскопических систем
- •2.2. Функции распределения
- •2.2.1. Общий подход
- •2.2.2. Функция распределения молекул идеального газа по модулю скорости молекул
- •2.2.3. График функции распределения молекул идеального газа по модулю скорости для двух температур
- •2.2.4. Функция распределения молекул идеального газа по кинетическим энергиям поступательного движения молекул
- •2.2.5. Средние характеристики молекул
- •Лекция 2
- •2.3. Основное уравнение мкт идеального газа для давления
- •2.4. Молекулярно-кинетический смысл температуры
- •2.5. Распределение Больцмана
- •2.5.1. Функция распределения Больцмана
- •2.5.2. Барометрическая формула
- •*2.7. Экспериментальная проверка распределения молекул по модулю скорости. Опыт Ламмерта
- •*2.8. Опыты Перрена по определению постоянной Авогадро
- •2.9. Основные понятия равновесной термодинамики
- •Лекция 3
- •2.10. Внутренняя энергия системы, работа, теплообмен
- •2.10.1. Внутренняя энергия системы
- •2.10.2. Работа
- •2.10.3. Теплообмен, теплоемкость системы
- •2.11. Первый закон (начало) термодинамики
- •2.12. Второе начало (закон) термодинамики. Термодинамические формулировки
- •2.13. Энтропия в термодинамике
- •Лекция 4
- •2.14. Качественный пример изменения энтропии при неравновесном процессе
- •2.15. Коэффициент полезного действия (кпд) идеального теплового двигателя
- •2.16. Число степеней свободы молекулы. Закон о равномерном распределении энергии по степеням свободы. Теплоемкость идеального газа
- •2. Молекула, состоящая из двух атомов
- •2.17. Применение первого и второго закона термодинамики к изопроцессам в идеальном газе
- •Лекция 5 *2.18. Примеры расчета изменения энтропии для неравновесных процессов.
- •2.19. Термодинамическая вероятность. Статистический смысл понятия энтропии.
- •2.20. Оценка термодинамической вероятности неравновесного и равновесного состояний.
- •Лекция 6
- •2.23. Основы физической кинетики
- •2.23.1. Уравнения для явлений переноса. Линейная неравновесная термодинамика
- •2.23.2. Формулы для коэффициентов переноса в случае идеального газа
- •2. Формулы для коэффициентов переноса
- •2.23.3. Зависимость коэффициентов переноса от параметров состояния идеального газа при протекании различных изопроцессов в идеальном газе
- •Лекция 7
- •2.24. Реальные газы. Уравнение Ван – дер - Ваальса
- •2.25. Экспериментальные и теоретические изотермы для реальных газов. Критическая точка
- •2.26. Внутренняя энергия реального газа
- •2.27. Жидкое состояние. Строение жидкости
2.2.2. Функция распределения молекул идеального газа по модулю скорости молекул
Пусть
идеальный газ (его молекулы на расстоянии
не взаимодействуют) находится в закрытом
сосуде в равновесном состоянии при
температуре
![]() .
.
Для
того чтобы ввести функцию распределения
молекул по модулю скорости, возьмем
произвольную молекулу идеального газа,
и через равные промежутки времени будем
измерять модуль ее скорости. Пусть из
общего числа N
опытов
![]() дает число опытов, в которых скорости
молекул попадают в интервал скоростей
(
дает число опытов, в которых скорости
молекул попадают в интервал скоростей
(![]() ,
,![]() +
+![]() ).
Тогда вероятность
).
Тогда вероятность
![]() попадания
скорости молекулы в малый интервал
скоростей будет равна
попадания
скорости молекулы в малый интервал
скоростей будет равна
![]()
при
стремлении общего числа опытов к
бесконечности (![]() ).
Это позволяет согласно формуле (2.2)
ввести функцию распределения молекул
по модулю скорости
).
Это позволяет согласно формуле (2.2)
ввести функцию распределения молекул
по модулю скорости
![]() .
(2.6)
.
(2.6)
Случайным
в выражении (2.6) является номер выбираемой
молекулы, над которой проводятся опыты,
а закономерным то, что вероятность
![]() попадания
значений скоростей молекулы в интервал
скоростей (
попадания
значений скоростей молекулы в интервал
скоростей (![]() ,
,![]() +
+![]() )
остается все время постоянной величиной
и не зависит от номера выбираемой
молекулы.
)
остается все время постоянной величиной
и не зависит от номера выбираемой
молекулы.
Итак,
функция
![]() является плотностью вероятности и равна
отношению вероятности
является плотностью вероятности и равна
отношению вероятности![]() попадания модуля скорости молекулы в
интервал скоростей (
попадания модуля скорости молекулы в
интервал скоростей (![]() ,
,![]() +
+![]() )
к величине этого интервала
)
к величине этого интервала![]() .
.
Можно
предложить другой способ определения,
другой физический смысл функции
распределения
![]() .
Для этого зафиксируем в какой-то момент
времени
скорости
всех молекул и нанесем их на ось скоростей
(рис. 2.2).
.
Для этого зафиксируем в какой-то момент
времени
скорости
всех молекул и нанесем их на ось скоростей
(рис. 2.2).
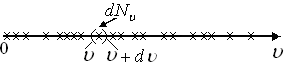
Рис. 2.2
Число
молекул
![]() ,
попадающих в интервал скоростей (
,
попадающих в интервал скоростей (![]() ,
,![]() +
+![]() ),
будет зависеть от общего числа молекул
),
будет зависеть от общего числа молекул![]() ,
от величины интервала скоростей
,
от величины интервала скоростей![]() и от скорости
и от скорости![]() ,
вблизи которой берется этот интервал.
Эту зависимость от скорости
,
вблизи которой берется этот интервал.
Эту зависимость от скорости![]() можно описать с помощью функции
можно описать с помощью функции![]() .
Тогда
.
Тогда
![]()
![]() .
(2.7)
.
(2.7)
Итак,
функция
![]() равна отношению относительного числа
молекул (
равна отношению относительного числа
молекул (![]() ),
скорости которых попадают в бесконечно
малый интервал скоростей (
),
скорости которых попадают в бесконечно
малый интервал скоростей (![]() ,
,![]() +
+![]() ),
к величине этого интервала
),
к величине этого интервала![]() .
.
Входящая
в формулы (2.6) и (2.7) функция
![]() получила название функции распределения
молекул по модулю скорости или функции
распределения Максвелла. Случайным в
формуле (2.7) являются номера молекул,
скорости которых попадают в заданный
интервал скоростей, а закономерным то,
что их число остается постоянным и не
зависит от номеров молекул. Формула для
этой функции была получена в 1859 г.
английским ученым Максвеллом и она
имеет вид:
получила название функции распределения
молекул по модулю скорости или функции
распределения Максвелла. Случайным в
формуле (2.7) являются номера молекул,
скорости которых попадают в заданный
интервал скоростей, а закономерным то,
что их число остается постоянным и не
зависит от номеров молекул. Формула для
этой функции была получена в 1859 г.
английским ученым Максвеллом и она
имеет вид:
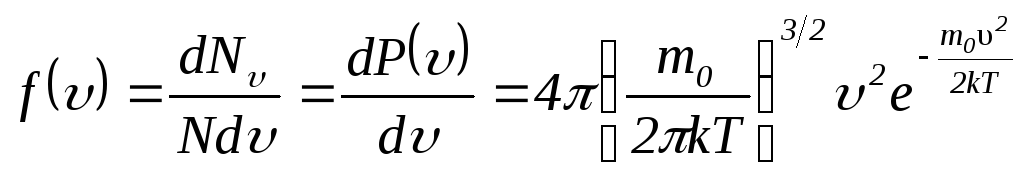 .
(2.8)
.
(2.8)
В
формуле (2.8)
![]() обозначает массу одной молекулы, а
обозначает массу одной молекулы, а![]() -
это постоянная Больцмана.
-
это постоянная Больцмана.
График
функции
![]() приведен
на рис. 2.3,а. Из него видно, что при скорости
молекулы
приведен
на рис. 2.3,а. Из него видно, что при скорости
молекулы![]() ,
равной нулю (
,
равной нулю (![]() ),
функция
),
функция![]() обращается в ноль, затем функция нарастает
и при скорости, называемой наиболее
вероятной
обращается в ноль, затем функция нарастает
и при скорости, называемой наиболее
вероятной
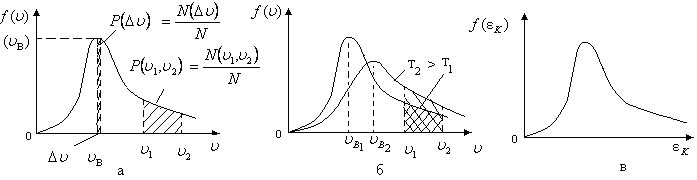 Рис.
2.3
Рис.
2.3
скоростью
![]() молекул, достигает максимального
значения, после этого она спадает до
нуля при скоростях молекул, стремящихся
к бесконечности.
молекул, достигает максимального
значения, после этого она спадает до
нуля при скоростях молекул, стремящихся
к бесконечности.
Зная
функцию распределения молекул идеального
газа по скоростям
![]() ,
можно найти относительное число молекул
,
можно найти относительное число молекул![]() ,
скорости которых попадают в интервал
скоростей (
,
скорости которых попадают в интервал
скоростей (![]() ,
,![]() ),
или вероятность попадания
),
или вероятность попадания![]() скорости одной молекулы в интервал
скоростей (
скорости одной молекулы в интервал
скоростей (![]() ,
,![]() ):
):
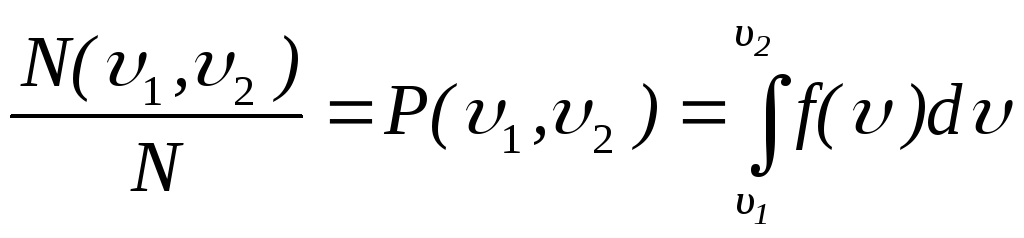 .
(2.9)
.
(2.9)
Графически
эта величина
![]() (или
(или
![]() )
представляет собой площадь под графиком
функции
)
представляет собой площадь под графиком
функции![]() в пределах интервала скоростей от
в пределах интервала скоростей от![]() до
до![]() (рис. 2.3,а). В случае малого интервала
скоростей
(рис. 2.3,а). В случае малого интервала
скоростей![]() (в его пределах функция распределения
(в его пределах функция распределения![]() остается примерно постоянной величиной)
можно с достаточной степенью точности
рассчитать относительное число (
остается примерно постоянной величиной)
можно с достаточной степенью точности
рассчитать относительное число (![]() )
молекул или вероятность
)
молекул или вероятность![]() по упрощенной формуле
по упрощенной формуле
![]() .
(2.10)
.
(2.10)
В этом случае площадь под графиком функции будет представлять собой площадь прямоугольной полоски (рис. 2.3,а).
Можно
дать пояснение названию наиболее
вероятной скорости
![]() молекул - если выбирать одинаковый
интервал скоростей
молекул - если выбирать одинаковый
интервал скоростей![]() около различных значений скорости
около различных значений скорости![]() ,
то вблизи скорости
,
то вблизи скорости![]() в малый интервал скоростей
в малый интервал скоростей![]() попадет наибольшее число молекул
(площадь прямоугольной полоски шириной
попадет наибольшее число молекул
(площадь прямоугольной полоски шириной![]() будет наибольшей).
будет наибольшей).
Площадь
под графиком функции распределения
![]() будет равна единице
будет равна единице
![]() ,
(2.11)
,
(2.11)
это выражение называют условием нормировки. Интеграл в формуле (2.11) представляет собой вероятность того, что скорость отдельной молекулы попадает в область всех возможных значений скоростей, а это является достоверным событием, вероятность которого равна единице.
По
другой трактовке функции распределения
![]() этот интеграл представляет собой
относительное число молекул, скорости
которых попадают в область всевозможных
значений скоростей, что приводит также
к единице в формуле (2.11).
этот интеграл представляет собой
относительное число молекул, скорости
которых попадают в область всевозможных
значений скоростей, что приводит также
к единице в формуле (2.11).
