
- •Модуль 2. Молекулярная физика Лекция 1
- •2.1. Статистический и термодинамический методы описания свойств
- •Макроскопических систем
- •2.2. Функции распределения
- •2.2.1. Общий подход
- •2.2.2. Функция распределения молекул идеального газа по модулю скорости молекул
- •2.2.3. График функции распределения молекул идеального газа по модулю скорости для двух температур
- •2.2.4. Функция распределения молекул идеального газа по кинетическим энергиям поступательного движения молекул
- •2.2.5. Средние характеристики молекул
- •Лекция 2
- •2.3. Основное уравнение мкт идеального газа для давления
- •2.4. Молекулярно-кинетический смысл температуры
- •2.5. Распределение Больцмана
- •2.5.1. Функция распределения Больцмана
- •2.5.2. Барометрическая формула
- •*2.7. Экспериментальная проверка распределения молекул по модулю скорости. Опыт Ламмерта
- •*2.8. Опыты Перрена по определению постоянной Авогадро
- •2.9. Основные понятия равновесной термодинамики
- •Лекция 3
- •2.10. Внутренняя энергия системы, работа, теплообмен
- •2.10.1. Внутренняя энергия системы
- •2.10.2. Работа
- •2.10.3. Теплообмен, теплоемкость системы
- •2.11. Первый закон (начало) термодинамики
- •2.12. Второе начало (закон) термодинамики. Термодинамические формулировки
- •2.13. Энтропия в термодинамике
- •Лекция 4
- •2.14. Качественный пример изменения энтропии при неравновесном процессе
- •2.15. Коэффициент полезного действия (кпд) идеального теплового двигателя
- •2.16. Число степеней свободы молекулы. Закон о равномерном распределении энергии по степеням свободы. Теплоемкость идеального газа
- •2. Молекула, состоящая из двух атомов
- •2.17. Применение первого и второго закона термодинамики к изопроцессам в идеальном газе
- •Лекция 5 *2.18. Примеры расчета изменения энтропии для неравновесных процессов.
- •2.19. Термодинамическая вероятность. Статистический смысл понятия энтропии.
- •2.20. Оценка термодинамической вероятности неравновесного и равновесного состояний.
- •Лекция 6
- •2.23. Основы физической кинетики
- •2.23.1. Уравнения для явлений переноса. Линейная неравновесная термодинамика
- •2.23.2. Формулы для коэффициентов переноса в случае идеального газа
- •2. Формулы для коэффициентов переноса
- •2.23.3. Зависимость коэффициентов переноса от параметров состояния идеального газа при протекании различных изопроцессов в идеальном газе
- •Лекция 7
- •2.24. Реальные газы. Уравнение Ван – дер - Ваальса
- •2.25. Экспериментальные и теоретические изотермы для реальных газов. Критическая точка
- •2.26. Внутренняя энергия реального газа
- •2.27. Жидкое состояние. Строение жидкости
2.23.2. Формулы для коэффициентов переноса в случае идеального газа
Рассмотрим вывод формул для коэффициентов переноса в случае идеального газа.
1. Средняя длина свободного пробега молекул газа. Молекулы идеального газа непрерывно хаотически движутся, сталкиваясь друг с другом. От одного столкновения до другого они движутся по прямой линии, а их общая траектория представляет собой ломаную линию, состоящую из прямолинейных участков
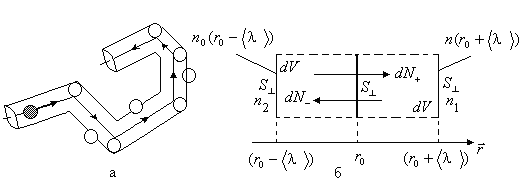
Рис. 2.16
(рис.
2.16,а). Под средней длиной свободного
пробега понимают величину, равную пути,
пройденному молекулой за время
![]() ,
деленному на число столкновений
,
деленному на число столкновений![]() ,
которое испытала молекула за это время
,
которое испытала молекула за это время![]()
![]() .
.
Выведем
формулу для средней длины свободного
пробега. Будем считать, что все молекулы
неподвижны, кроме одной молекулы. За
время
![]() молекула пройдет расстояние
молекула пройдет расстояние![]() ,
где
,
где![]() -
средняя арифметическая скорость
молекулы. Причем она за это время
-
средняя арифметическая скорость
молекулы. Причем она за это время![]() испытает столкновения со всеми молекулами,
центры которых попадают внутрь коленчатого
цилиндра (его радиус равен диаметру
одной молекулы, а длина образующей
цилиндра равна пройденному молекулой
расстоянию
испытает столкновения со всеми молекулами,
центры которых попадают внутрь коленчатого
цилиндра (его радиус равен диаметру
одной молекулы, а длина образующей
цилиндра равна пройденному молекулой
расстоянию![]() ,
рис. 2.16,а). Число столкновений движущейся
молекулы будет равно количеству молекул,
центры которых попали в этот цилиндр
,
рис. 2.16,а). Число столкновений движущейся
молекулы будет равно количеству молекул,
центры которых попали в этот цилиндр
![]() ,
,
что позволяет записать
![]() ,
(2.77)
,
(2.77)
где
в формулу (2.77) введен коэффициент
![]() ,
учитывающий движения всех молекул - в
этом случае нужно для определения числа
столкновений
,
учитывающий движения всех молекул - в
этом случае нужно для определения числа
столкновений![]() использовать относительную скорость
молекул, а не скорость молекул относительно
стенки сосуда. Это приводит к следующим
формулам:
использовать относительную скорость
молекул, а не скорость молекул относительно
стенки сосуда. Это приводит к следующим
формулам:
![]()
![]() ,
,
где
учтено, что усреднение слагаемого
![]() по всевозможным углам
по всевозможным углам![]() (
(![]() )
дает нулевое значение (
)
дает нулевое значение (![]() ).
).
2. Формулы для коэффициентов переноса
*2.1.
Вывод формулы для коэффициента диффузии.
Пусть в идеальном газе создано
неравномерное распределение концентрации
молекул, а именно, на одной стенке
прямоугольного сосуда концентрация
молекул газа будет равной
![]() ,
а на другой -
,
а на другой -![]() (рис. 2.16). Тогда в газе возникает явление
диффузии (точнее, самодиффузии). Выберем
площадку
(рис. 2.16). Тогда в газе возникает явление
диффузии (точнее, самодиффузии). Выберем
площадку![]() ,
перпендикулярную направлению переноса
(рис. 2.16,а). Будем считать, что все молекулы,
пересекающие эту площадку
,
перпендикулярную направлению переноса
(рис. 2.16,а). Будем считать, что все молекулы,
пересекающие эту площадку![]() ,
испытывают последнее столкновение на
одном и том же расстоянии
,
испытывают последнее столкновение на
одном и том же расстоянии![]() от нее, равном средней длине свободного
пробега:
от нее, равном средней длине свободного
пробега:![]() (рис. 2.16,а). Тогда число молекул
(рис. 2.16,а). Тогда число молекул![]() ,
пересекающих площадку в положительном
направлении оси
,
пересекающих площадку в положительном
направлении оси![]() ,
будет определяться концентрацией
молекул на расстоянии (
,
будет определяться концентрацией
молекул на расстоянии (![]() ),
а в обратном направлении (
),
а в обратном направлении (![]() )
– (
)
– (![]() ).
За время
).
За время![]() через площадку
через площадку![]() пройдет
пройдет![]() часть всех молекул, попадающих в объемы
часть всех молекул, попадающих в объемы![]() по разные стороны от площадки. Поэтому
суммарный перенос молекул за это время
будет равен
по разные стороны от площадки. Поэтому
суммарный перенос молекул за это время
будет равен
![]()
![]() .
.
Из записанной выше формулы видно, что коэффициент диффузии будет определяться выражением
![]() .
(2.78)
.
(2.78)
Ввиду
малости расстояния
![]() при выводе формулы (2.78) было использовано
следующее равенство:
при выводе формулы (2.78) было использовано
следующее равенство:![]() .
.
2.2.
Формулы для коэффициентов вязкости
![]() и теплопроводности
и теплопроводности![]() можно вывести
аналогично:
можно вывести
аналогично:
![]() ,
(2.79)
,
(2.79)
![]() .
(2.80)
.
(2.80)
В
формулу для коэффициента теплопроводности
![]() входит удельная теплоемкость
входит удельная теплоемкость![]() идеального газа при постоянном объеме,
которую согласно формулам (2.38) и (2.57,б)
можно представить в следующем виде:
идеального газа при постоянном объеме,
которую согласно формулам (2.38) и (2.57,б)
можно представить в следующем виде:
![]() .
(2.81)
.
(2.81)
