2.17. Применение первого и второго закона термодинамики к изопроцессам в идеальном газе

Запишем, прежде всего, формулы, которые будут использоваться при рассмотрении изопроцессов в идеальном газе.

, ,,, (2.57а)

, ,. (2.57б)

К этим формулам добавлено уравнение состояния идеального газа (2.37) - уравнение Менделеева – Клапейрона.

1.1. Изотермический процесс (). Уравнение процесса:.

,,,, (2.58а)

, . (2.58б)

Отметим, что молярная теплоемкость при этом процессе равна бесконечности, так как любой подвод тепла идет на совершение газом работы и при этом температура системы не изменяется.

1.2. Изохорический процесс (). Уравнение процесса:.

, ,,, (2.59а)

, (2.59б)

. (2.59в)

1.3. Изобарический процесс (). Уравнение процесса:.

, ,, (2.60а)

, (2.60б)

, (2.60в)

. (2.60г)

Отметим, что разность теплоемкостей идля идеального газа равна

. (2.61)

Это уравнение (2.61) получило название уравнения Майера.

1.4. Адиабатический процесс (изоэнтропийный процесс, ) - это процесс, происходящий в системе без теплообмена с внешними телами, или это изоэнтропийный процесс, при его протекании энтропия системы не изменяется.

, ,,, (2.62а)

, . (2.62б)

Выведем формулу уравнения адиабатического процесса

Итак, уравнение адиабаты в параметрах состояния () принимает вид:

, (2.63а)

а для других параметров идеального газа запишется таким образом:

. (2.63б)

При выводе был введен коэффициент Пуассона , который равен отношению молярной теплоемкости идеального газа при постоянном давлении к молярной теплоемкости газа при постоянном объеме

, (2.64)

причем он выражается через число степеней свободы молекулы идеального газа.

В координатах () адиабата изменяется более резко, чем изотерма, так как коэффициент Пуассонабольше единицы (, рис. 2.13,а).

Использование уравнения адиабаты помимо формулы (2.62,а) позволяет получить следующую формулу для работы идеального газа при адиабатическом процессе:

. (2.65)

Лекция 5 *2.18. Примеры расчета изменения энтропии для неравновесных процессов.

Если необходимо рассчитать изменение энтропии произвольного н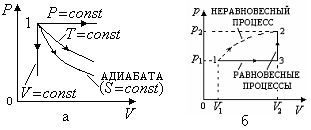еравновесного процесса перехода системы (идеальный газ) из одного состояния (параметры состояния) в другое (параметры состояния), необходимо использовать тот факт, что энтропия является функцией состояния системы, и рассчитать

Рис. 2.13 изменение энтропии для

равновесного процесса перехода. Этот процесс наиболее удобен, так как состоит из нескольких изопроцессов (например, изобарический 1-3, и изохорический 3-2, рис. 2.13,б), что позволяет использовать формулы, приведенные в п. 2.2.4 пункт 1 (,)

. (2.66)

Как видно, в расчетную формулу (2.66) входят только параметры начального и конечного состояний.

Если в процессе теплообмена системы с внешними телами происходит нагревание (охлаждение), плавление (кристаллизация) вещества, превращение жидкости в пар (или конденсация), то необходимое для расчета изменение энтропии и количество теплотырассчитываются по формулам (2.39), (2.40).

В качестве примера рассмотрим процесс, происходящий в системе за счет теплообмена с внешними телами, процесс нагревания льда массы от температуры() до температуры(при этой температуре лед превращается в воду). Тогда для расчета изменения энтропии системы мы используем равновесные процессы и рассчитываемследующим образом:

. (2.67)