Лабораторная работа № 3

Представление алгоритмов с помощью блок-схем

Цель работы

Получить практические навыки представления алгоритмов с помощью блок-схем.

Порядок выполнения работы

1. Ознакомьтесь с заданиями на лабораторную работу. Изучите примеры решения задач.

2. Для каждого задания выполните постановку задачи, опишите метод решения задачи и представьте алгоритм решения задачи в виде блок-схемы.

3. Проверьте результат работы алгоритма «вручную», подобрав в качестве исходных данных небольшие значения или значения, для которых результат известен заранее.

Примеры решения задач

1. Даны три числа x, y, z. Найти максимальное из них.

Постановка задачи:

Входные данные: x, y, z – три числа.

Выходные данные: max – максимальное число.

Метод решения:

Сначала сравним числа x и y; max присвоим максимальное значение из них. Затем сравним z и max; если z больше, то присвоим max значение z, если нет, то ничего не делаем. В результате max – максимальное число.

Блок-схема:

.

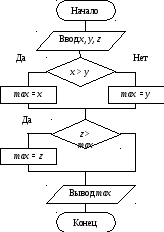2. Даны два числа a и b. Вычислить сумму всех натуральных чисел в диапазоне от a до b.

Постановка задачи:

Входные данные: a, b – два натуральных числа.

Выходные данные: sum – сумма чисел.

Метод решения:

Для данной задачи воспользуемся циклом с параметром. Сначала присваиваем sum значение 0, т.к. в этой переменной мы будем накапливать сумму. Затем в цикле от a до b с шагом 1 будем к значению sum прибавлять значение i (i – это переменная цикла, которая в нашем случае будет принимать значения от a до b). В результате, в sum получим искомую сумму чисел.

Блок-схема:

.

3. Найти сумму всех элементов массива A, больших заданного числа.

Постановка задачи:

Входные данные: A – массив чисел; n – количество элементов массива;

chis – заданное число.

Выходные данные: Sum – сумма чисел.

Метод решения:

Для данной задачи воспользуемся циклом с параметром. Сначала вводим массив из n элементов. Затем вводим заданное число chis. Далее присваиваем Sum значение 0, т.к. в этой переменной мы будем накапливать сумму. Затем в цикле от 1 до n с шагом 1 будем сравнивать элементы массива с заданным числом; если очередной элемент массива A[i] больше chis, то прибавляем его к сумме Sum, иначе – ничего не делаем. В результате, в Sum получим искомую сумму элементов массива.

Блок-схема:

.

Результаты работы

Отчет оформить в текстовом редакторе Word. Для каждой задачи в отчете должны быть:

• постановка задачи (входные и выходные данные);

• метод решения (словесное описание алгоритма);

• блок-схема.

Контрольные вопросы

1. Откуда появилось слово алгоритм?

2. Перечислите свойства алгоритма.

3. В чем состоит структурный подход к проектированию программ?

4. Чем реализуются повторные вычисления при проектировании программ?

5. В чем особенности циклов с предусловием и постусловием?

6. В чем отличие цикла с параметром от цикла с условием?

7. Какую структуру циклического алгоритма Вы использовали для решения своей задачи? Почему?

Варианты заданий

Условия

1. Определить, является ли треугольник со сторонами a, b, c равнобедренным.

2. Определить, является ли треугольник со сторонами a, b, c равносторонним.

3. Даны три числа a, b, c. Определить, существует ли треугольник со сторонами a, b, c.

4. Даны действительные числа a, b, c, x, y. Выяснить, пройдет ли кирпич с ребрами a, b, c в прямоугольное отверстие со сторонами x, y. Наклонно кирпич не просовывать.

5. Даны действительные числа Х и У (ХУ). Меньшее из этих двух чисел заменить их полусуммой, а большее – их удвоенным произведением.

6. Определить, является ли введенное число числом Амстронга. Числом Амстронга называется число, равное сумме своих цифр в степени их количества. Например: 153= 1³+5³+3³

7. Даны три вещественных числа x, y, z. Вычислить значения выражений x + y + z и xyz; определить максимальное из них.

8. Определить, принадлежит ли точка с координатами x, y фигуре, заданной левой полуокружностью и вертикальной прямой, проходящей через центр окружности. Координаты центра окружности и радиус произвольные.

9. Составьте алгоритм для упорядочивания трех чисел a, b, c по возрастанию таким образом, чтобы букве а соответствовало наименьшее число, букве b – среднее, а букве c – наибольшее.

10. В каждый подпрочный набор входят 1 ручка, 2 линейки, 4 тетрадки. Имеется а линеек, b тетрадей, c ручек. Сколько получится наборов?

11. Определить, является ли число а делителем числа b.

12. Три отрезка заданы координатами своих концов. Определить, во сколько раз наибольший из них больше наименьшего.

13. Даны две точки: A(x1, y1) и B(x2, y2). Составить алгоритм, определяющий, которая из точек находится ближе к началу координат.

14. Даны три числа. Возвести в квадрат те из них, значения которых неотрицательны, и в четвертую степень – отрицательные.

15. Даны целые числа m, n. Если числа не равны, то заменить каждое из них одним и тем же числом, равным большему из исходных, а если равны, то заменить число нулями.

16. Посчитать количество отрицательных среди чисел a, b, c.

17. Заданы три положительных числа a, b и с. Определить, являются ли они последовательно стоящими членами арифметической или геометрической прогрессии. Если являются, то вычислить разность или знаменатель прогрессии.

18. Посчитать количество целых среди чисел a, b, c.

19. Определить делителем каких чисел a, b, c является число k.

20. Услуги телефонной сети оплачиваются по следующему правилу: за разговоры до А минут – В рублей, а разговоры сверхустановленной нормы оплачиваются из расчета С рублей за минуту. Составить алгоритм программы, вычисляющей плату за пользование телефоном для введенного времени разговоров за месяц.

21. Перераспределить значения переменных x и y так. чтобы в x оказалось большее из этих значений, а в y – меньшее.

22. Заданы два натуральных числа. Определить является ли среднее арифметическое этих чисел целым числом.

23. Заданы три стороны треугольника a, b и с. определить является ли этот треугольник прямоугольным и какая сторона является гипотенузой.

24. Заданы два целых числа. Определить, являются ли они оба четными или оба нечетными или какое из них четное, а какое нечетное.

Циклы

1. Дано натуральное число n. Вычислить: .

2. Найти сумму –1² + 2² - 3² + 4² - …+10². Условную инструкцию не использовать.

3. Найти сумму 1  2 + 2  2² + 3  2³ + … + n  2ⁿ .

4. Найти сумму .

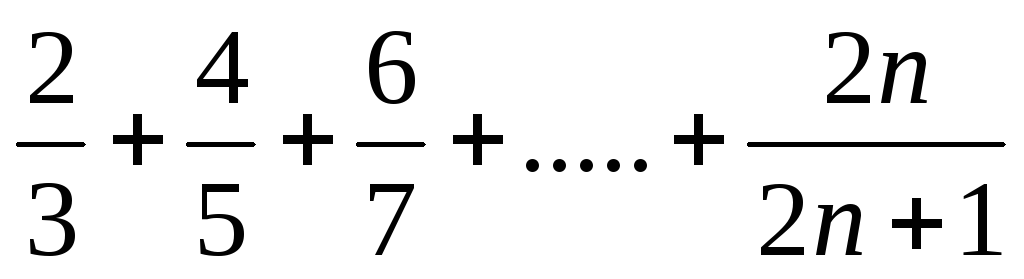5. Найти сумму 1 2 + 2 3 4 + 3 4 5 6 +… + N (N+1) …  2N.

6. Ввести натуральное число N>2. Выбрать все простые числа в интервале от 2 до N.

7. Среди чисел 1 < n < 100 найти все пары чисел, для которых их сумма равна их произведению.

8. Заданы два целых числа А и В. Определить НОД(А,В).

9. Определить количество трехзначных натуральных чисел, сумма цифр которых равна n (1  n  27). Операции деления, div, mod не использовать.

10. Вычислить сумму и произведение 10 членов арифметической прогрессии 2, 5, 8, 11, …

11. Подсчитать сумму всех нечетных чисел от 101 до 301.

12. Известно, что:

1³ = 1

2³ = 3 + 5

3³ = 7 + 9 + 11

4³ = 13 + 15 + 17 + 19 и т.д.

Определить значение n³, не используя операции умножения.

13. Начав тренировки, лыжник в первый день пробегал 10 км. Каждый следующий день он увеличивал длину пробега на 10% от предыдущего дня. Определить, в какой день он пробежит больше 20 км, в какой день суммарный пробег за все дни превысит 100 км.

14. Вычислить функцию .

15. Дано натуральное число n. Вычислить .

16. Среди чисел 1 < n < 100 найти все пары чисел, для которых их сумма равна их произведению.

17. Найти сумму 1 2 + 2 3 4 + 3 4 5 6 +… + N (N+1) …  2N.

18. Определить сколько из n заданных точек принадлежит графику функции y = |x|.

19. Даны натуральные числа n и k. Вычислить .

20. Вычислить сумму при х = 2.

21. Дано натуральное число n < 99. Получить все способы выплаты суммы n с помощью монет достоинством 1, 5, 10, 20 коп.

22. Составить программу возведения натурального числа в квадрат, использую следующую закономерность:

1² = 1

2² = 1 + 3

3² = 1 + 3 + 5

4² = 1 + 3 + 5 + 7 и т.д.

23. Ввести натуральное число N>2. Выбрать все простые числа в интервале от 2 до N.

24. Составить алгоритм программы, помогающей вкладчику узнать, сколько нужно ожидать суммы S, если начальный вклад равен V при P процентах прироста вклада в год.

25. Определить, сколько из n заданных точек принадлежит графику функции y = |x|.

Дополнительные задания

26. Сколько можно купить быков, коров и телят, если бык стоит 10 рублей, корова – 5 рублей, теленок – полтинник (0,5 рубля), при условии, что на 100 рублей надо купить 100 голов скота.

27. Даны натуральные числа N и М (МN). Определить, сколько из чисел N, N+1, … , M являются номерами високосных годов.

28. Даны натуральные числа N и М. Получить сумму М последних цифр числа N.

29. Создать программу расчета факториала.

30. Найти все простые делители заданного натурального числа.

31. Вычислить .

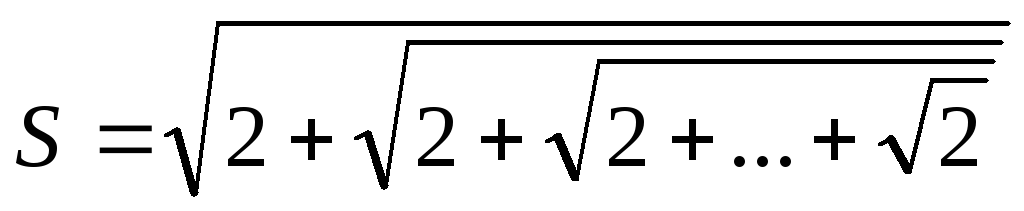32. Вводится последовательность из n целых чисел. Найти сумму всех отрицательных.

33. Вычислить сумму и произведение 10 членов арифметической прогрессии 2, 5, 8, 11, … .

34. Составить алгоритм программы определения номера геометрической прогрессии 2, 4, 8, 16, …, превышающего число z.

Информационные технологии 8