Геометрическая лаговая структура Койка
Пример: изучается
зависимость
– ввод основных фондов в t-м
году от
–
капитальные
вложения в предыдущие годы. Строится
все долго, поэтому предположим
существование сколь угодно больших
лагов.
.
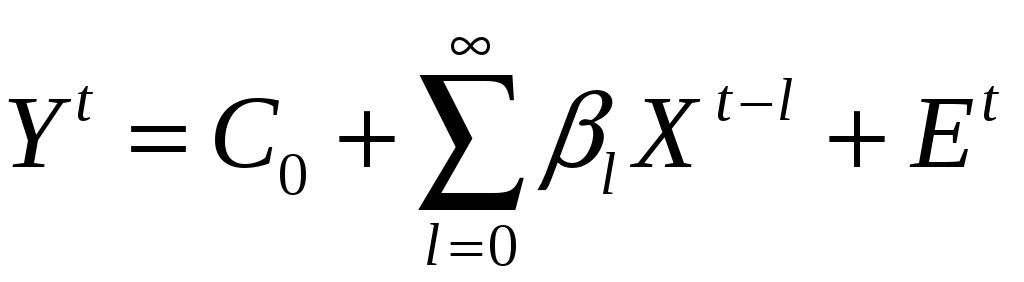Л. Койк (1954 г.) предположил:
,
l = 0, 1, 2... ,
(0 < λ < 1) – знаменатель геометрической прогрессии,
, (19)
,
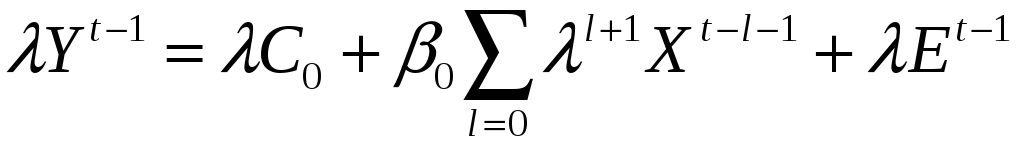, (20)
.
(19) – (20):
,
. (21)
Определение: модель вида
,
(22)
включающую
объясняющую эндогенную лаговую переменную
,
называют моделью Койка.
Замечание:
в модели зачастую коррелирует с
и c
(автокорреляция), например, см. (21):
.
Это делает невозможным применение
обычного МНК в оценке 3 коэффициентов
в (22), и методы идентификации модели
Койка зависят от свойств
.
Модель частичной корректировки
Пример: изучается
зависимость выпуска
некоторого
товара от спроса
на
него. Очевидно, спрос определяет
–
оптимальный выпуск товара;
; (23)
а фактический
выпуск:
,
где
– сила интуиции и/или возможности
предприятия.
подставляем в
(23):
.
Это частный случай модели Койка с ошибкой, одномоментно не коррелированной с Yt-1. Оценки МНК асимптотически несмещенные.
Пример ([2], табл. 6.9, с. 198):
Данные по экономике США (млрд $):
–
расходы на жилье;
–
личный доход;
–
индекс цен на жилье
в процентах к 1972 г.
Если строить
регрессию
на
и
,
то получим:
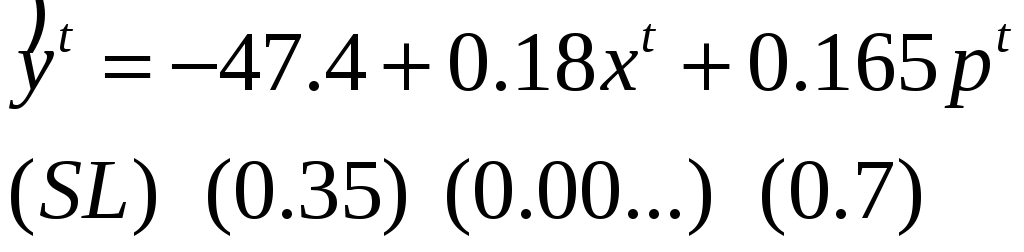
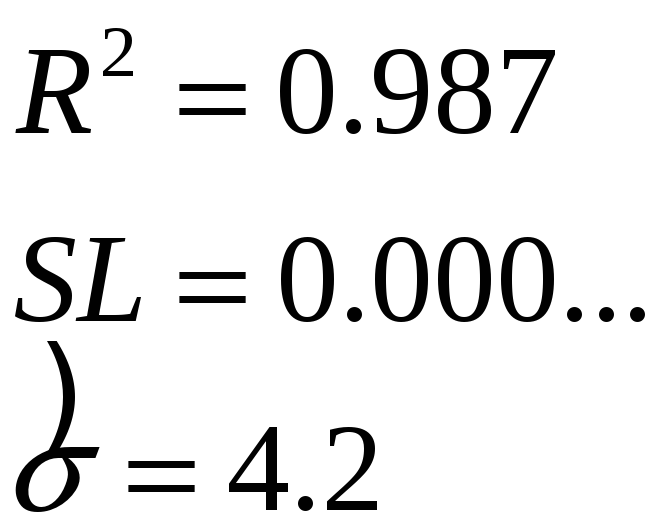
Знак перед
бессмысленен!
,
–
ошибки
автокоррелированы, оценки неэффективны.
Если строить
регрессию
на
,
и
,
то получим:
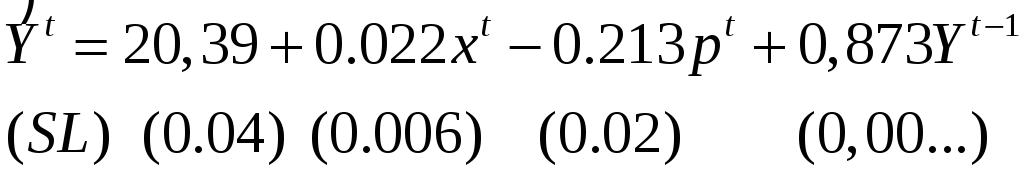
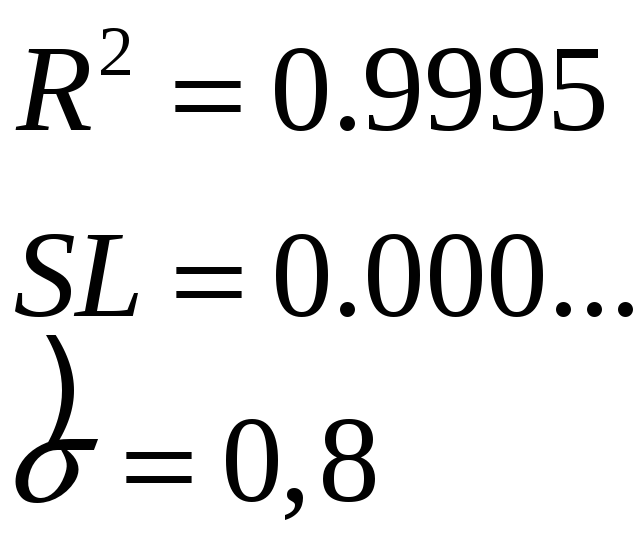
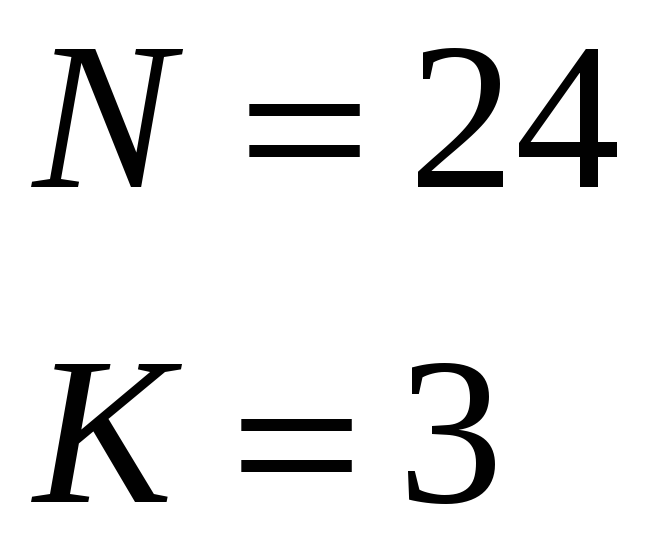
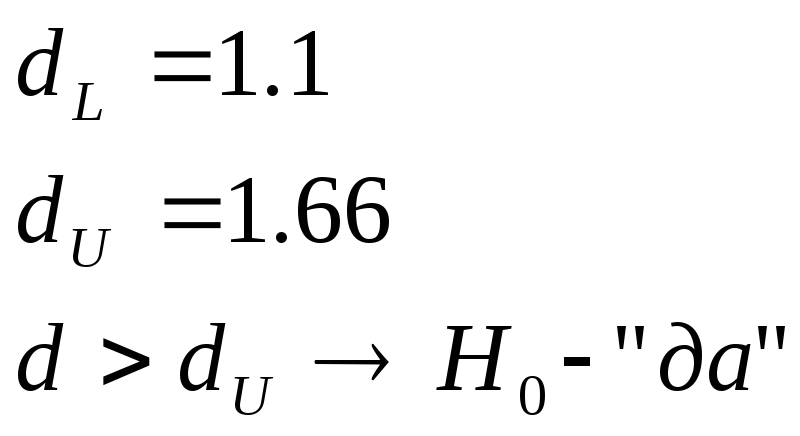ошибки не
автокоррелированы.
Поскольку
,
то оценка корректирующего множителя
(то есть население США медленно
корректирует вложения в жилье при
изменении личного дохода и цен на жилье);
оценка оптимальных вложений в жилье:
,
где
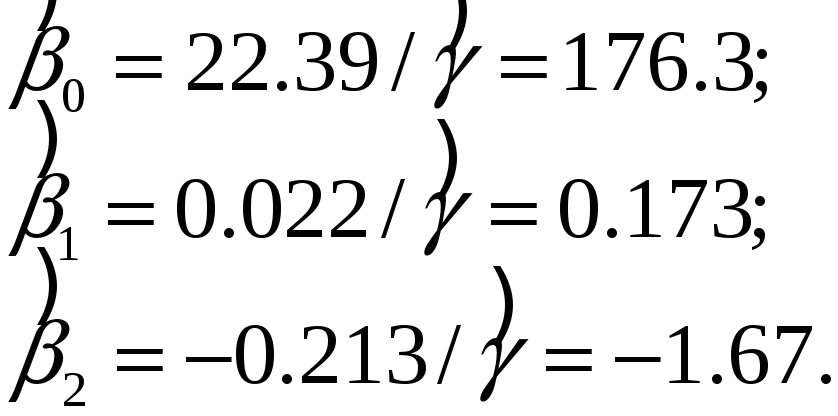
Замечание: модели частичной корректировки следует использовать, когда ясна связь факторов с идеализированной характеристикой, а наблюдаемая результирующая характеристика лишь частично корректируется в сторону идеализированной.
Модель адаптивных ожиданий
Пример: пусть
изучается зависимость инвестиций
от банковской учетной ставки
.
На самом деле инвесторы исходят из
ожидаемой банковской учетной ставки
в предстоящем году.
;
(24)
саму величину они
определяют так:
(т. е. люди неохотно отказываются от
своих представлений (ожиданий));
;
;
.
Подставим это в (24):
– это ведет к
модели Койка с ошибками, коррелированными
с лаговой
переменной.
Модель нелинейна
по параметрам, значит, вместо обычного
МНК следует применять нелинейный (по
параметру
)
МНК:
(модели
);
;
,
(25)
.
Пример: модель гиперинфляции Ф. Кейгана (1956 г.).
Исследовалось 7 периодов гиперинфляции в США (1921–1956 гг.),
временной шаг был
1 мес.,
– ожидаемый уровень инфляции на следующий
месяц. Кейган разумно считал, что чем
выше уровень инфляции в следующем
месяце, тем меньше спрос на деньги.
,
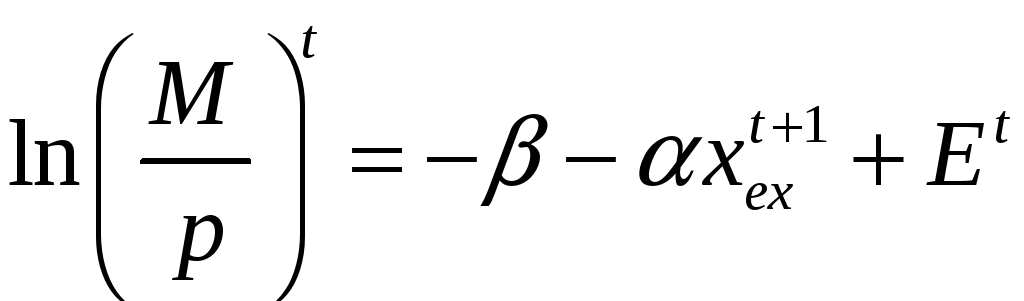где
– индекс изменения объема денег в
обращении;
– индекс цен.
Поскольку
ненаблюдаемая, то для нее применялась
модель адаптивных ожиданий, далее
использовался нелинейный МНК. Результат:
,
.
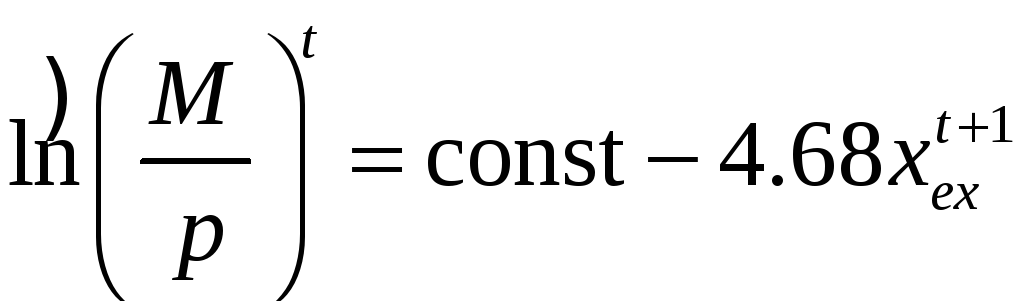Если
(10 %), то спрос на деньги будет на 37,4 %
меньше, чем при стабильных ценах (
):
.
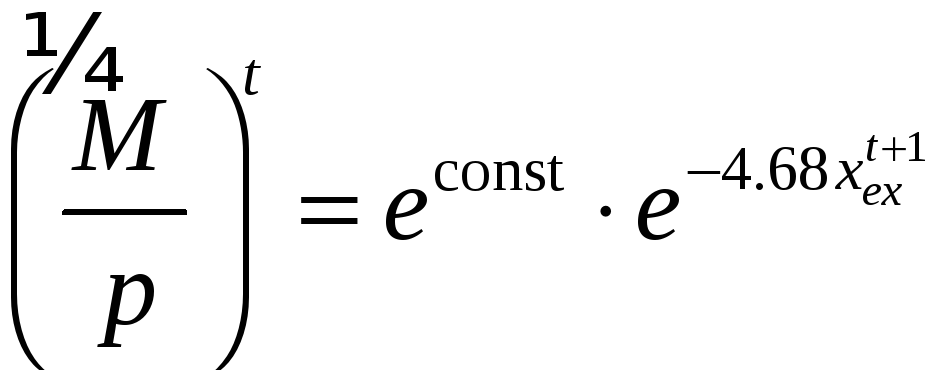