
- •Определение цены опциона методом имитационного моделирования
- •Общие принципы имитационного моделирования многокомпонентных систем
- •Организация квазипараллелизма просмотром активностей
- •Два способа изменения (протяжки) системного времени
- •Организация квазипараллелизма транзактным способом
- •Оценка погрешности результирующего показателя имитации из-за различия затравочных чисел генератора псевдослучайных чисел
- •Понижение дисперсии при вычислении интегралов
- •Применение имитационного моделирования (им) к сравнению методов оценивания и анализу их точности
- •Основная литература
- •Дополнительная литература
- •Обобщенный мнк
- •1) Гетероскедастичные ошибки.
- •3. Объясняющие переменные и случайные ошибки одномоментно некоррелированы (хотя в разные моменты и зависимы).
- •Адекватность моделирования. Состоятельные методы
- •Оптимальный предиктор
- •Алгоритм чередующихся математических ожиданий – ace-алгоритм (alternating conditional expectations)
- •Проверка адекватности моделирования
- •Полиномиальная лаговая структура Алмон
- •Геометрическая лаговая структура Койка
- •Модель частичной корректировки
- •Модель адаптивных ожиданий
- •Модель потребления Фридмена
3. Объясняющие переменные и случайные ошибки одномоментно некоррелированы (хотя в разные моменты и зависимы).
Пример:
![]() ,
,
![]() – лаговая объясняющая
переменная, ясно, что она зависит от
– лаговая объясняющая
переменная, ясно, что она зависит от
![]() ,
но не от
,
но не от
![]() .
.
![]() – только
асимптотически (в больших выборках)
несмещенные.
– только
асимптотически (в больших выборках)
несмещенные.
Адекватность моделирования. Состоятельные методы
Цели моделирования бывают двух видов:
Прогноз (algoritmic modeling): например, нейронные сети.
Знание механизма
(data modeling):
![]()
Пример: опасность (несостоятельность) упрощённого data modeling.
Система
![]() ,
,
![]()
Модель
![]() .
.
По данным
![]() оцениваем
оцениваем
![]() .
.
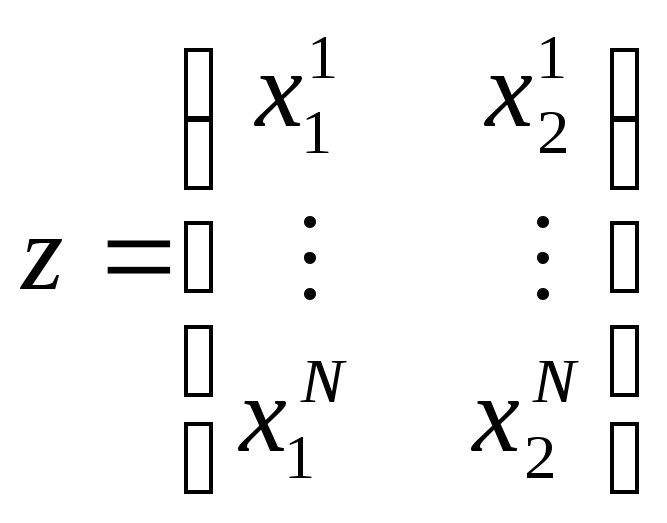 ,
,
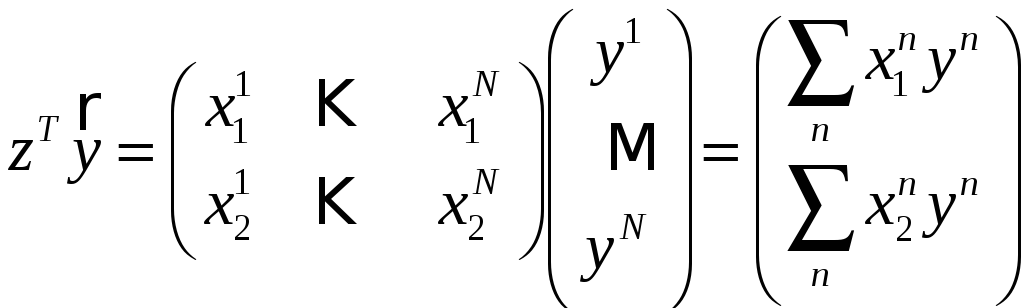 ;
(9)
;
(9)
![]()
![]()
![]()
![]() ;
;
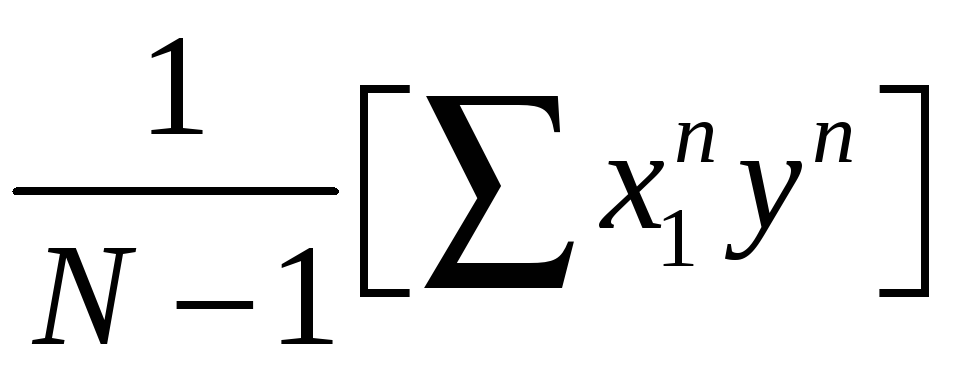 – несмещенная и
состоятельная оценка
– несмещенная и
состоятельная оценка
![]() ,
т.е. ковариации, которая равна 0, значит,
(9)
,
т.е. ковариации, которая равна 0, значит,
(9)![]() .
.
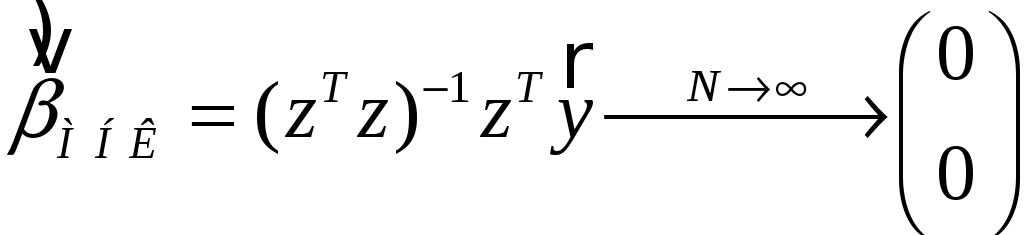 ,
и может сложиться мнение, что Y
вообще не зависит от X1
и X2 !
,
и может сложиться мнение, что Y
вообще не зависит от X1
и X2 !
Если проверить гипотезу
![]() :
:
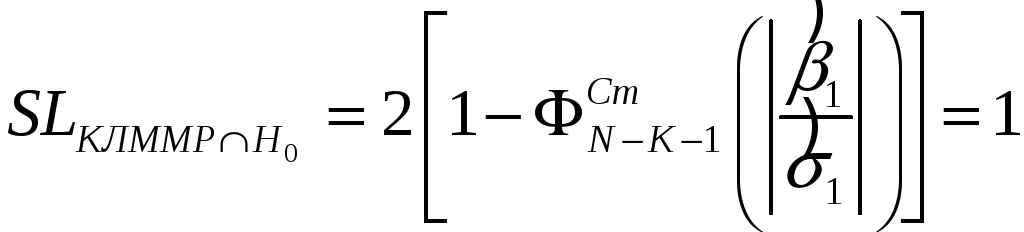 ,
то результат H0 –
“да”, т. е. если модель линейна, то β1
может быть равен 0.
,
то результат H0 –
“да”, т. е. если модель линейна, то β1
может быть равен 0.
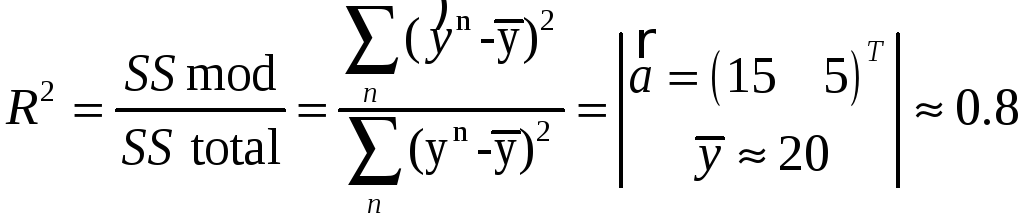 и, казалось бы,
оцененная модель
и, казалось бы,
оцененная модель
![]() хорошо описывает данные! Оговорка: когда
хорошо описывает данные! Оговорка: когда
![]() ,
нельзя гарантировать, что
,
нельзя гарантировать, что
![]() .
.
Таким образом, если не обратить внимания на оговорки, то можно сделать в корне неверные выводы о системе.
Оптимальный предиктор
Пусть
![]() и
и
![]() – зависимые случайные величины.
– зависимые случайные величины.
Задача: составить
оптимальный прогноз
![]() величины Y по известному
значению x величины
X.
величины Y по известному
значению x величины
X.
![]() – ошибка прогноза
(случайная величина), поэтому точность
прогноза целесообразно характеризовать
средним квадратом ошибки при данном
значении x:
– ошибка прогноза
(случайная величина), поэтому точность
прогноза целесообразно характеризовать
средним квадратом ошибки при данном
значении x:
![]()
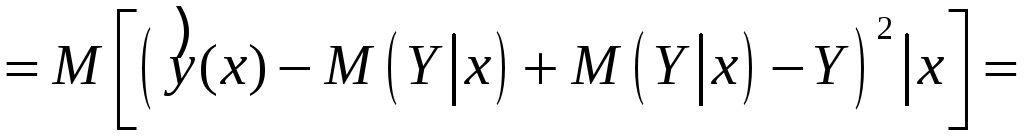
![]()
![]() .
.
Поставим задачу:
![]() .
.
Видно, что ее
решение:
![]() .
Таким образом, доказана следующая ниже
теорема.
.
Таким образом, доказана следующая ниже
теорема.
Теорема:
оптимальным прогнозом величины
![]() по
данному значению x
является прогноз по регрессии.
по
данному значению x
является прогноз по регрессии.
Замечание:
если ставить задачу минимизации средней
ошибки прогноза при всевозможных X,
т. е.
![]() ,
то ясно, что если регрессия является
лучшим прогнозом при каждом
,
то ясно, что если регрессия является
лучшим прогнозом при каждом
![]() ,
то и в среднем тоже.
,
то и в среднем тоже.
Следствие:
оптимальным предиктором
![]() в смысле минимизации средней ошибки
прогноза при всех
в смысле минимизации средней ошибки
прогноза при всех
![]() является функция регрессии
является функция регрессии
![]() .
.
Пример: Пусть
![]() ,
где
,
где
![]() ,
,
![]() ,
- все независимые случайные величины.
Какой предиктор X1
или X2 лучше?
(Сравнить корреляционные отношения).
,
- все независимые случайные величины.
Какой предиктор X1
или X2 лучше?
(Сравнить корреляционные отношения).
Пусть
![]() –
результирующая величина. Не будем
ограничивать себя только линейными
моделями, наоборот, рассмотрим зависимость
вида
–
результирующая величина. Не будем
ограничивать себя только линейными
моделями, наоборот, рассмотрим зависимость
вида
![]() ,
(10)
,
(10)
![]() – любые функции:
– любые функции:
![]() .
.
Доля дисперсии, не объясненная регрессией (10):
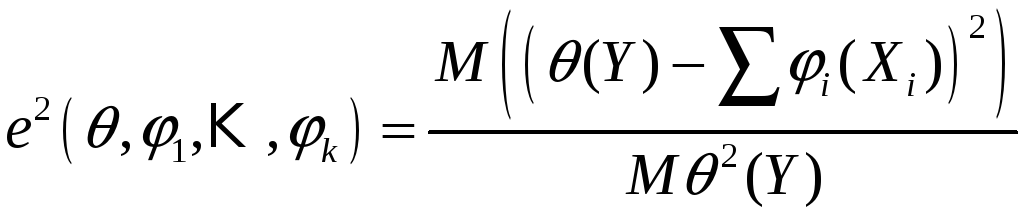 (11)
(11)
Определение:
назовем оптимальными преобразованиями
те
![]() ,
которые минимизируют (11):
,
которые минимизируют (11):
![]() .
.
Алгоритм чередующихся математических ожиданий – ace-алгоритм (alternating conditional expectations)
Л. Брейман и Дж. Фридман в 1985 г. предложили итеративный алгоритм нахождения оптимальных преобразований [18].
Пусть распределение
![]() известно,
известно,
![]() .
(12)
.
(12)
Рассмотрим случай
![]()
![]() .
(13)
.
(13)
Минимизируем (13)
по
![]() при
фиксированном
при
фиксированном
![]() при
условии (12). Решение, как мы знаем, есть
функция регрессии:
при
условии (12). Решение, как мы знаем, есть
функция регрессии:
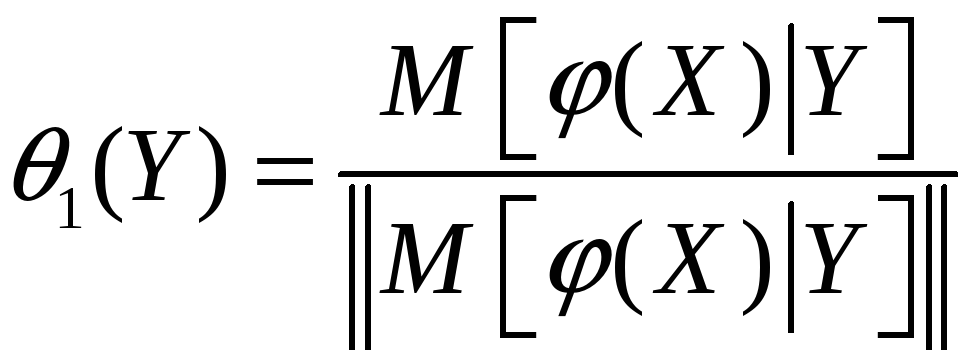 ,
,
![]() .
.
Минимизируем (13)
по
![]() при
фиксированном
при
фиксированном
![]() .
Решение есть:
.
Решение есть:
![]() .
.
Это является базисом алгоритма:
1. Положить
![]() .
.
2. do
while
![]() уменьшается:
уменьшается:
![]() .
.
Заменить
![]() на
на
![]() ;
;
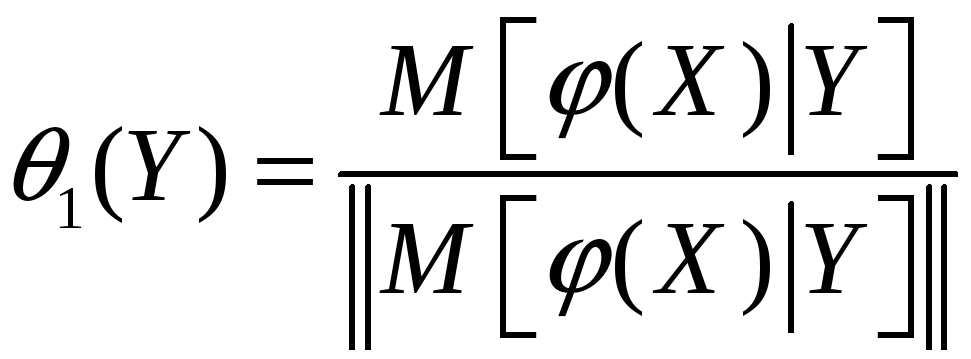 .
.
Заменить
![]() на
на
![]() .
.
3. end while
4.
![]() – решения (
– решения (![]() )
)
5. Конец алгоритма.
Этот алгоритм
можно обобщить на случай
![]() –
регрессоров.
–
регрессоров.
При практическом применении алгоритма совместные распределения всех величин известны редко, вместо них – данные в виде выборки.
![]() ,
и все величины заменяем выборочными
оценками:
,
и все величины заменяем выборочными
оценками:
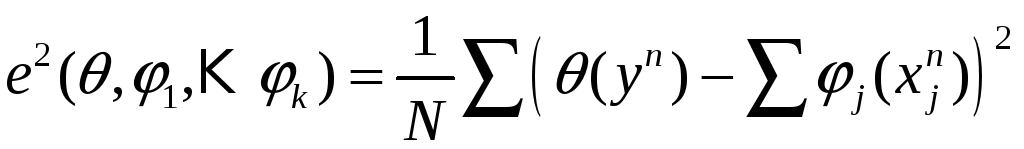 ;
;
![]() :
:
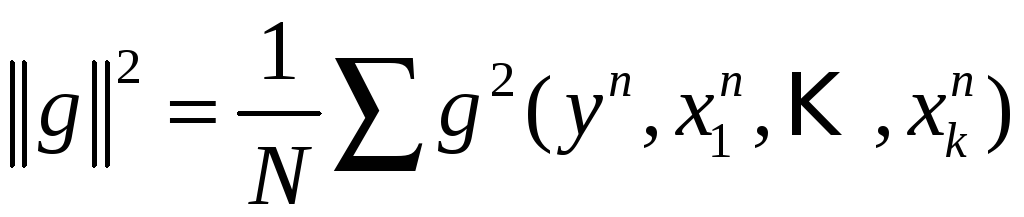 .
.
Если один из
факторов категоризованный (![]() ),
то
),
то
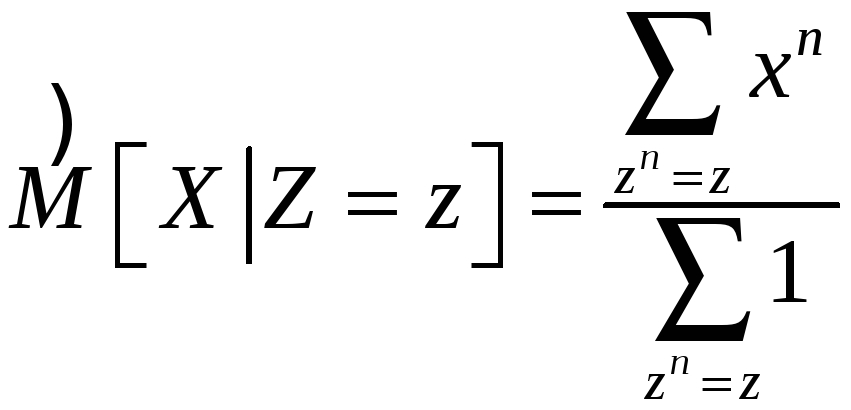 ,
где суммы берутся по поднабору, имеющему
категоризованное значение Z
= z.
,
где суммы берутся по поднабору, имеющему
категоризованное значение Z
= z.
Если обе переменные количественные, то
![]() =
выборочному среднему
=
выборочному среднему
![]() – значений
– значений
![]() с
номерами, соответствующими
с
номерами, соответствующими
![]() ближайшим по значению к
ближайшим по значению к
![]() .
.
Алгоритм оценивает
![]() при всех соответствующих значениях
данных
при всех соответствующих значениях
данных
![]() .
.
Замечание: прогноз после ACE можно сделать так:
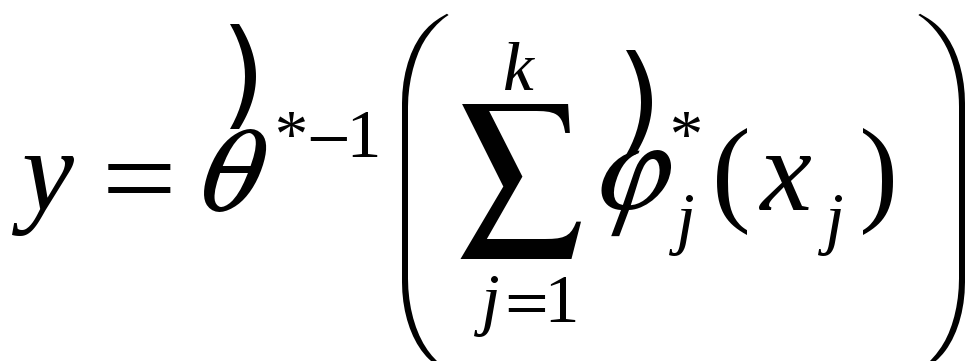 , где xj
известны.
, где xj
известны.
Пример (заимствован из [18]): исследовалась зависимость стоимости жилья от разнообразных факторов. Прежними исследователями была предложена функциональная зависимость:
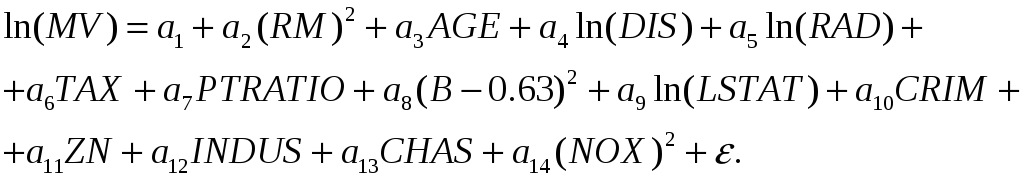 (14)
(14)
Факторы: RM – число комнат на человека, DIS – расстояние до работы, PTRATIO – отношение числа учеников к числу учителей в школе, B – доля темнокожего населения, LSTAT – доля населения с низким статусом, CRIM – уровень преступности, NOX – концентрация оксидов азота.
Данные по 506
наблюдениям были подвергнуты ACE , где
использовались переменные
![]() .
Если бы модель (14) соответствовала
данным, то
.
Если бы модель (14) соответствовала
данным, то
![]() были бы линейными функциями. Это оказалось
не так. В частности:
были бы линейными функциями. Это оказалось
не так. В частности:
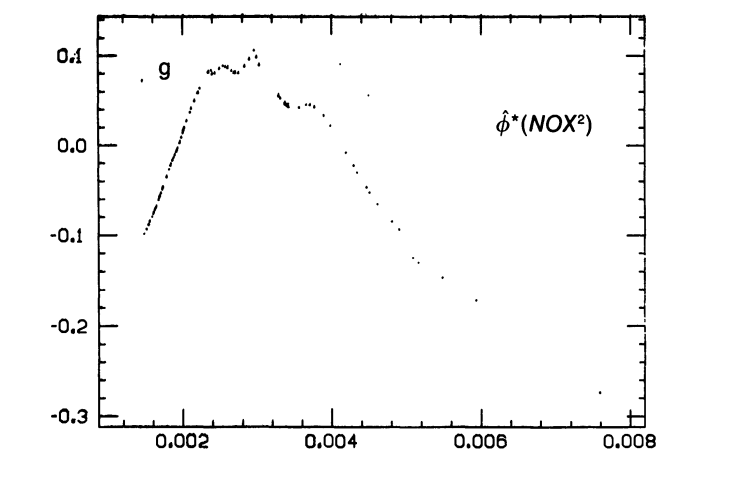
то есть при малых концентрациях NOX стоимость растет с ростом концентрации, а при больших – падает. Следует отметить, что сам по себе вклад фактора NOX весьма мал по сравнению с важнейшими факторами.
