If you test the hypothesis
:
,
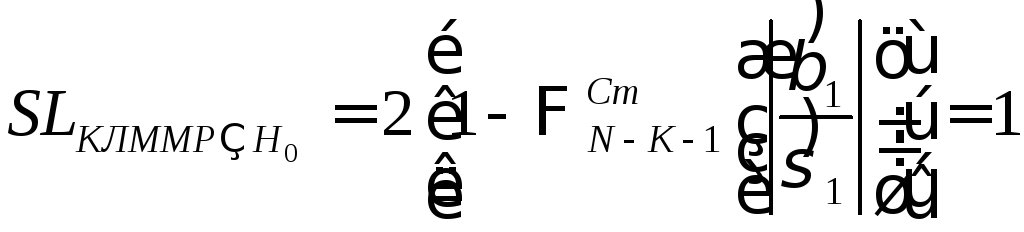the result H0
– “yes ”, so If the model is linear, β1
may be equal to 0.
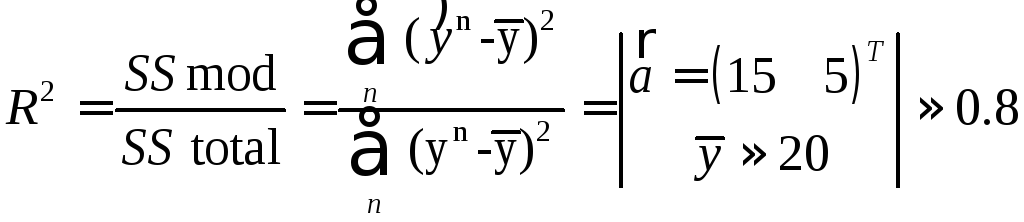and, it
would seem, the estimated model 
describes well the data!
Disclaimer:
when 
,
is no guarantee that 
.
Thus, if you do not pay attention to the reservation, it can be fundamentally wrong conclusions about the system.
Optimal predictor
Optimal Let - dependent random variables.
Problem:
make the best forecast 
of Y from the known value x of X.
–forecast
error (random variable), so it is advisable to characterize the
accuracy of the prediction mean square error for a given value of x:
.
We pose the
problem:
.
It can be
seen that its solution:
.
Thus we have proved the following theorem below.
Theorem: Thus we have proved the following theorem below.
Note:
With the goal of minimizing the average prediction error for all
possible X so. 
,
it is clear that if the regression is a better prognosis for each,
then the average too.
Corollary:
the best predictor of 
in the sense of minimizing the average prediction error for all is
the regression function 
.
Example:
,
where
,
,
- all independent random variables. Which predictor X1 or X2 is
better? (Compare the correlation relationship).
Let Y - the resultant value. We will not limit ourselves to linear models, on the contrary, we consider the dependence of the form
,
(10)
–any
functions:
.
The proportion of variance unexplained by regression (10):
(11)
Definition:
is called the optimal transformation 
,
that minimizes (11):
.
Alternating algorithm of expectations - ACE-algorithm (alternating conditional expectations)
L. and J. Breyman. Friedman in 1985 suggested an iterative algorithm for finding the optimal transformation [18].
Let the
distribution 
is known,
.
(12)
Consider the case
.
(13)
Minimize
(13) by 
a fixed 
under the condition (12). The solution, as we know, is a function of
regression:
,
.
Minimize
(13) by 
with
fixed 
.
There is a solution:
.
This is the basis of the algorithm:
1. Put 
.
2. do
while
decreases:
.
Swap
on
;
.
Swap 
with
.
3. end while
4.
– solution (
)
5. End algorithm.
This algorithm can be generalized to the case K - the covariates.
In the practical application of the algorithm joint distribution of all variables known rare, instead of them - the data as a sample.
,
and all values are replaced sample estimates:
;
:
.
If one of the factors categorized (Z), then
,
where the sums are taken over the subset having categorized the value
Z = z.
If both variables are quantitative, the
=
the sample mean
–values
with numbers corresponding to 
closer to 
.
The
algorithm assesses 
with all the relevant data values 
.
Note: prognosis after ACE can do this:
, wherexjwe know.
Example (taken from [18]): investigated the dependence of the cost of housing a variety of factors. Previous researchers had proposed functional dependence:
(14)
Factors: RM - the number of rooms per person, DIS - distance to work, PTRATIO - the ratio of students to the number of teachers in the school, B - the proportion of the black population, LSTAT - proportion of the population with low status, CRIM - crime rate, NOX - the concentration of nitrogen oxides .
Data on 506
observations were subjected to ACE, which used variables 
.
If the model (14) fit the data, then 
are linear functions. It was not. In particular:
ie, at low concentrations of NOX value increases with increasing concentration, while at high - falls. It should be noted that by itself contribute factor NOX is very small in comparison with the most important factors.
The validation of the simulation
Adequacy - line model of the real system.
can not
serve as indicators of adequacy, as the model is actually estimated
from the condition SSres
-> min, and these figures are always decent. But this rigid
adherence to the training data, and how the data at all (new) - is
unclear.
The figure asterisks show the data on which the model was estimated. She describes them well and SSres will be small. Circles show the new data that are likely to be poorly described, ie. E., The estimated model is not adequate to the real system.
To check the adequacy can:
- Or wait for the arrival of new data;
- or reserve a portion of the original data as exams:
:
.
Basic and,
in essence, the only indicator of the adequacy of the model (in case
of linearity)
,
– “standard
error of the adequacy ”.
Compared
with 
– standard error of the approximation –
,
but that it indicates the prediction error:
,
~ 95 % interval.
Sliding test (cross-validation)
To improve
the reliability determination
do so:
1) split the sample into parts;
2) train at all, except for the first part, to examine the first;
3) train at all, except for the second, to examine the second;
4) and so on
5) train at all, except the last, examine the last;
6) count;
.
Bootstrap procedure
If N is
small, to improve the reliability
You can use the procedure bootstrap:
1) make the training set with the return of randomly selected - elements;
2) to train the model on this set;
3) examine a model for the rest of the data in the set do not fall;
4) repeat S times.
Model with lagged variables
ExaMPLE:
study the dependence of
– population's total expenses in
-year
from 
– observed income for previous years. Since an accumulation, ie. E.
Spending immediately, but after some time lag, we arrive at the
model:
(15)
,
;
where 
– the share of income that is spent through 
years after its acquisition,
–delay
();
–max delay;
–error
pattern in the time 
(unaccounted factors) does not depend on 
;
,
(16)
–consumption
observed at zero income.
,
.
In
principle, the model (15, 16) is KLMMR if 
not random or stochastic model with independent variables,
uncorrelated with errors.