Решение_MB_15770 (1)

Задание 2

Определить взаимное расположение следующих пар прямых:

а)

б)

Решение

А) Направляющий вектор первой прямой , направляющий вектор второй прямой , так как , значит, данные прямые пересекаются

Б) Приведем второе уравнение прямой к общему виду

, а первое уравнение прямой сократим на 3 и получим , тогда получаем, что данные прямые являются параллельными.

Задание 3

Известно, что диагонали параллелограмма ABCD пересекаются в точке М(1,6), а его стороны проходят соответственно через точки Составить уравнения сторон этого параллелограмма.

Решение

Обозначим координаты точек как .

Найдем точки на прямых соответственно симметричные относительно точки М. Точка М будет являться серединой отрезков , тогда, получаем

Прямая АВ проходит через точки , тогда получаем

Прямая BC проходит через точки , тогда получаем

Прямая CD проходит через точки , тогда получаем

Прямая AD проходит через точки , тогда получаем

Задание 4

Найти проекцию точки Р(-8,12) на прямую, проходящую через точки А(2,- 3) и В(- 5.1). Система координат прямоугольная.

Решение

Составим уравнение прямой, проходящую через точки

Прямая, перпендикулярная данной записывается в виде , где коэффициент найдем из того факта, что точка лежит на перпендикулярной прямой, то есть , значит, уравнение перпендикулярной прямой есть . Найдем точку пересечения прямых

То есть, проекция точки Р на прямую АВ есть точка

Задание 5

Определить положение точки М(-3, 2) относительно треугольника, стороны которого заданы уравнениями

Решение

Е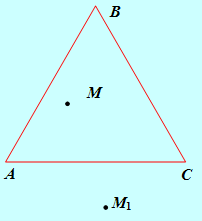сли точка М расположена внутри треугольника АВС, то ее отклонение δ от каждой стороны треугольника имеет тот же знак, что и для вершины, не лежащей на этой стороне, а если точка М лежит вне треугольника, то по крайней мере с одной из вершин она окажется в разных полуплоскостях относительно стороны треугольника.

Пусть первое уравнение задает сторону АВ, второе – ВС, третье – АС. Найдем координаты точек А, В и С:

Для ответа на вопрос задачи отметим, что:

1) если точка М расположена внутри треугольника АВС, то ее отклонение δ от каждой стороны треугольника имеет тот же знак, что и для вершины, не лежащей на этой стороне (т. е. точка М расположена относительно каждой стороны треугольника в одной полуплоскости с третьей вершиной);

2) если точка М лежит вне треугольника, то по крайней мере с одной из вершин она окажется в разных полуплоскостях относительно стороны треугольника (на рисунке: точки М₁ и В расположены по разные стороны от прямой АС).

Составим нормальные уравнения сторон треугольника АВС:

Вычислим соответствующие отклонения:

1) для точек М и А относительно прямой ВС:

2) для точек М и В относительно прямой АС:

3) для точек М и С относительно прямой АВ:

Итак, точки М и А и М и С лежат по разные стороны от прямой ВС и АВ соответственно. Следовательно, точка М расположена вне треугольника АВС.

Задание 6

Основанием равнобедренного треугольника служит прямая , а боковой стороной - прямая . Составить уравнение другой его боковой стороны, зная, что она проходит через точку (3,1).

Решение

Найдем точку пересечения основания и боковой стороны

Через точку проведем прямую, параллельную основанию. Прямая будет иметь вид

Найдем точку пересечения этой прямой с известной боковой стороной

Найдем середину отрезка между боковыми сторонами

Прямая, проходящую через точку перпендикулярная основанию является и высотой и медианой. Уравнение этой прямой имеет вид

Найдем точку пересечения основания и высоты

Данная точка является серединой отрезка между двумя вершинами основания, тогда так как нам известна одна из вершин, то вычислим вторую

Составим уравнение боковой стороны через точки и

Задание 7

Составить уравнение биссектрисы острого угла между прямыми

Решение

Найдем точку пересечения двух прямых

Направляющий вектор первой прямой есть , второй , так как их скалярное произведение положительно , поэтому найдем уравнение биссектрисы между векторами , проходящую через точку

Направляющий вектор биссектрисы угла равен сумме нормированных направляющих векторов сторон

Так как точка лежит на этой биссектрисе, то

Задание 8

Составить уравнение плоскости, которая проходит через точку параллельно плоскости

Решение

Плоскость, параллельная записывается в виде , где коэффициент найдем из того факта, что точка лежит в этой плоскости, то есть , значит, уравнение плоскости есть