
Решая систему (14), получим
![]() .
(15)
.
(15)
Зная J и MT, можно рассчитать среднеквадратичное отклонение S, которое характеризует среднюю степень отклонения экспериментальных результатов от прямой М=МТ+J .
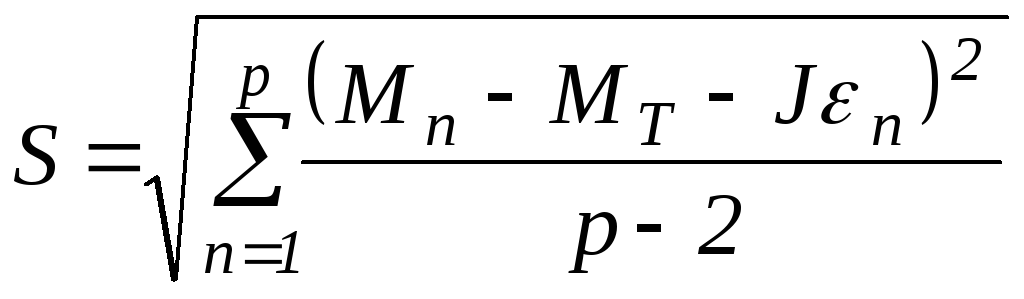 .
(16)
.
(16)
Среднеквадратичные отклонения величин J и MT определяются по следующим формулам:
 .
(17)
.
(17)
Наконец, доверительные интервалы для J и MT при выбранной доверительной вероятности рассчитываются таким образом
![]() .
(18)
.
(18)
то есть коэффициент Стъюдента выбирается по таблице для эффективной вероятности (1+)/2 и для числа точек на два меньшего, чем при обработке. Например, если надо найти доверительные интервалы при выбранной доверительной вероятности =0,90 для параметров J и MT, полученных при обработке 10 точек (p=10), то в формулу (18) должно подставляется значение коэффициента Стъюдента t0.95, 8.
Итак, имеющиеся в распоряжении три экспериментальные зависимости М от следует обработать методом наименьших квадратов, применяя формулы (15) – (18). Используя полученные значения моментов инерции системы и моментов сил трения, надо построить наилучшие прямые и сравнить их с соответствующими экспериментальными зависимостями.
Далее необходимо
рассчитать величины ![]() и
и ![]() ,
а также их погрешности. Это, очевидно,
можно сделать по следующим формулам:
,
а также их погрешности. Это, очевидно,
можно сделать по следующим формулам:
![]() .
(19)
.
(19)
Здесь J0
и J0
– значение момента инерции и погрешность
этой величины для маятника без грузов.
Подставляя в (19) вместо J
и J
значения момента инерции и его погрешности,
рассчитанные по методу наименьших
квадратов для маятника Обербека при
максимальном расстоянии между грузами,
получаем ![]() и
и ![]() .
Аналогично получаются значения
.
Аналогично получаются значения ![]() и
и ![]() .
.
Теперь можно
провести корректное сравнение полученных
значений момента инерции со значениями
![]() и
и ![]() ,
рассчитанными по формуле (3).
,
рассчитанными по формуле (3).
Приложение 1
Вычислим момент инерции цилиндра длиной L и радиусом R относительно оси Z, проходящей через центр масс перпендикулярно оси цилиндра (рис.3).
Согласно формуле (29) введения для однородного тела
![]() ,
(20)
,
(20)
где x и y– координаты элементарного объемчика dV.
Для определения dV разобьем цилиндр на тонкие диски длиной dx. На таком диске выделим узкий кольцевой слой радиусом r и шириной dr. В свою очередь на этом кольцевом слое выделим двумя радиусами, угол между которыми составляет малую величину d , кольцевой сектор. Поскольку размеры этого сектора очень малы, мы не допустим большой ошибки, если его объем dV будем рассчитывать как объем куба со сторонами rd , dr и dx. Таким образом, элементарно малый объем можно представить в следующем виде: dV=rdrdx
Интегрирование по всему объему кольца эквивалентно тройному интегрированию: по в пределах от 0 до 2, по r в пределах от 0 до R, и по x - в пределах от -L/2 до L/2. Однако для того, чтобы выполнить это интегрирование надо переменную y записать через переменные r и . Как видно из рис.3, эти переменные связаны соотношением y=rSin. Таким образом, интеграл (20) можно записать так
![]()
Учитывая, что Sin2=(1-Cos2)/2, в результате интегрирования получаем

![]() (21)
(21)
Эта формула позволяет рассчитать момент инерции сплошного однородного цилиндра по известным геометрическим размерам и массе цилиндра (нетрудно заметить, что R2L - это масса цилиндра). Формулу для момента инерции коаксиального цилиндра с внешним радиусом R, внутренним радиусом r и массой можно получить, используя принцип суперпозиции, согласно которому J=JR -Jr. Здесь JR , Jr – моменты инерции цилиндров с радиусами R и r соответственно. Очевидно, что длины и плотности этих цилиндров одинаковы. Тогда, в соответствии с (21), получаем
![]()
![]()
Величина (R2-r2) - это площадь основания коаксиального цилиндра, (R2-r2)L - это объем коаксиального цилиндра, а (R2-r2)L - это масса коаксиального цилиндра - . Таким образом, для момента инерции коаксиального однородного цилиндра получаем следующую формулу
![]() .
(22)
.
(22)
