
- •If (n&1){ . . .} – проверяет, является ли n нечётным.
- •If (n&m){ . . .} - проверяет, есть ли у n и m совпадающие соответствующие биты.
- •If (n&(n-1)){ . . .}– проверяет, что n не является степенью 2. Если n есть степень 2, то n представляется в двоичном виде:
- •Void inint (tip n, char s[])
- •Void inint16(tip n, char s[])
- •Число –3.5: с0 0с 00 00 00 00 00 00
- •Double сохраняется в памяти 15-16 десятичных знаков. Выполнение операций над числами, представленными с плавающей точкой(говорят- в плавающей арифметике).
- •Достоинства формы представления чисел с плавающей точкой.
- •Недостатки формы представления чисел с плавающей точкой:
Лекция 1. Битовые операции.
Битовые (поразрядные) операцииприменяются к целым операндам и выполняются над их двоичными представлениями. Стандартные типы , кроме вещественных, в С++ являются целыми, т.е. к данным этих типов (int, short, char, bool) могут быть применены поразрядные операции. Выполняется битовая операция над соответствующими битами операндов и результат операции записывается в соответствующий бит результата.
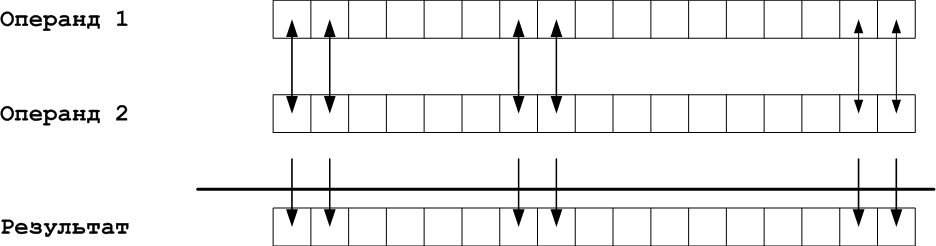
Рисунок 1. Схема битовой операции
Операции:
&- поразрядная конъюнкция (И) двоичных представленийоперандов целого типа. Бит результата равен 1 тогда и только тогда, если соответствующие биты операндов равны 1.
7 & 5= 5 7: 00000111
5: 00000101
Результат 5:00000101
Операция используется для выделения из битового представления части разрядов, такие разряды умножаются на 1 (по операции &).
| – поразрядная дизъюнкция (ИЛИ) двоичных представлений операндов целого типа. Бит результата равен 1, если хотя бы один из соответствующих битов операндов равен 1.
7 | 5= 7 7: 00000111
5: 00000101
Результат 7: 00000111
Операция используется для приформирования 1 некоторым разрядам битового представления, к этим разрядам добавляются 1 (по операции |).
^ - поразрядное исключающее ИЛИ двоичных представлений операндов целого типа. Бит результата равен 1, если соответствующие биты операндов различны.
7 ^ 5= 2 7: 00000111
5: 00000101
Результат 2: 00000010
Операция используется для инвертирования некоторых разрядов битового представления, такие разряды в операции исключающего ИЛИ обрабатываются 1.
~ - поразрядное отрицание (одноместная операция) инвертирует каждый разряд двоичного представления операнда.
~ 5 =-6 5: 00000101
Результат - 6 : 11111010 –дополнительный код числа -6
Операции сдвига
Применяются к целочисленным операндам:
ОП1 << ОП2 (сдвиг влево) или ОП1 >> ОП2(сдвиг вправо)
Двоичное представление ОП1 сдвигается влево (<<)) или вправо (>>) на количество двоичных разрядов, равное второму операнду ОП2.
При сдвиге вправоосвободившиеся разряды заполняются знаковым разрядом (при сдвиге знаковых операндов) и нулём для беззнаковых. Вышедшие за разрядную сетку биты теряются.
5>>2 = 1 00000101 =>00000001 - результат = 1
(-5)>>2 = -2 11111011 =>11111110 - дополнительный код -2.
При сдвиге влево освободившиеся разряды заполняются нулями.
5<<2 = 00000101 =>00010100 - результат = 20
(-5)<<2 = 11111011 =>11101100 - дополнительный код -20
Операция сдвига влево целого числа на к разрядов эквивалентна умножению числа на 2k, а сдвига вправо - делению числа на 2k, но операции сдвига выполняются быстрее, чем умножение или деление.
Однако при сдвиге влево в знаковый бит может попасть цифровой разряд числа, это ситуация переполнения, она не замечается, но получившийся результат не равен умножению числа на 2k.
cout<<(2147483647<<1)<<" "<<(-2147483647<<1)<<'\n'; // результат -2 2
Не следует путать битовые операции с логическими:
!0 – имеет значение истины, а ~0 представляет конечную последовательность единиц(т.е. -1).
cout<<(!0)<<" "<<(~0)<<'\n'; результат : 1 -1
Примеры использования битовых операций:
unsigned int n,m; (или int n,m; но n,m –не отрицательные)
If (n&1){ . . .} – проверяет, является ли n нечётным.
If (n&m){ . . .} - проверяет, есть ли у n и m совпадающие соответствующие биты.
If (n^m){ . . .} - проверяет, есть ли у n и m несовпадающие соответствующие биты.
If (n&(n-1)){ . . .}– проверяет, что n не является степенью 2. Если n есть степень 2, то n представляется в двоичном виде:
n: 00…01000…000,
а n-1: 00…00111…111,
их произведение n&(n-1)=0.
Битовые операции и операции сдвига используются часто
в выражениях, где они предпочтительнее других операций, т.к. выполняются быстрее;
для реализации множеств небольшого размера. Множество представляется в виде конечной последовательности битов (вектора битов), бит есть элемент множества, каждому биту соответствует элемент некоторого, например, массива чисел, размер множества чисел ограничен количеством битов в векторе.
A[n-1]A[n-2] . . . . . . . . . . . . . . . . . . . . A[2] A[1] A[0]
-
1
0
0
0
1
1
0
Оператор typedef служит для того, чтобы задать новое имя некоторому типу: typedef тип новое_имя [размерность];
Например:
typedef int tip; // стандартный тип int назван новым именем tip. Алгоритм описывается для этого нового имени tip. В дальнейшем, если необходимо алгоритм использовать для нового имени, например short, надо будет изменить только оператор typedef: typedef short tip;
Размерность необязательна. Новое имя может использоваться также, как стандартные имена:
typedef char tipmas [50]; // tipmas это char[50]
tipmas M[20]; M – это массив из 20 строк по 50
символов. (char MM [20][50])
const int L=sizeof(tip);
//Внутреннее представление целых данных
typedef int tip;
Void inint (tip n, char s[])
{ // Двоичное представление целого данного n в строке s
int i, l;
l=sizeof(tip)<<3; // размер битовой строки для типа tip
i=l-1; // l-ый разряд- конец строки
do
{ s[i--]=(char)((n&1)+'0'); //формирование i-го символа
n=n>>1; //сдвиг числа n вправо
}
while (i>=0); //цикл пока все символы не сформируются
s[l]=0; //символ 0 в конце сформированной строки
}
Void inint16(tip n, char s[])
{// 16-теричное представление целого n в строке s.
int i,l;
char alf[]="0123456789ABCDEF"; // 16-ричный алфавит
l=sizeof(tip)<<1; //размер 16-теричной строки для tip
i=l-1;
do
{s[i--]=alf[n&15]; //формирование i-го символа
n=n>>4; //сдвиг числа n вправо
}
while (i>=0); //цикл пока все символы не сформируются
s[l]='\0'; //символ 0 в конце сформированной строки
}
Пример. Внутреннее представление целого числа -123 в слове: - 123=-7В16= -111 10112
-123: 11111111 11111111 11111111 10000101
-123 в16-ом коде: FF FF FF 85
Алгоритм “Быстрая степень”
Рассмотрим возведение an, где n- целое, положительное число. Алгоритм основан на двоичном представлении показателя n.
n= nk*2k + nk-1*2k-1 +. . . . ni*2i+. . . .n1*21+ n0+20
![]()
Вычисление этого произведения представляется тремя параллельными процессами:
вычисление ni – цифр двоичного представления показателя n, они получаются как остатки от деления на 2 сначала n, а потом частных от делений, пока не получится частное, равное нулю, остатки в порядке получения n0 n1 n2 . . .nk-1 nk (см. перевод целого в двоичную систему).
параллельно с этим процессом строятся степени: a=a*a
![]() .
.
Кроме того, происходит накопление произведения в некоторой переменной p (в начале p=1;): если остаток ni равен нулю, соответствуюшая степень не учитываертся в произведении, если ni ≠0, то p=p*
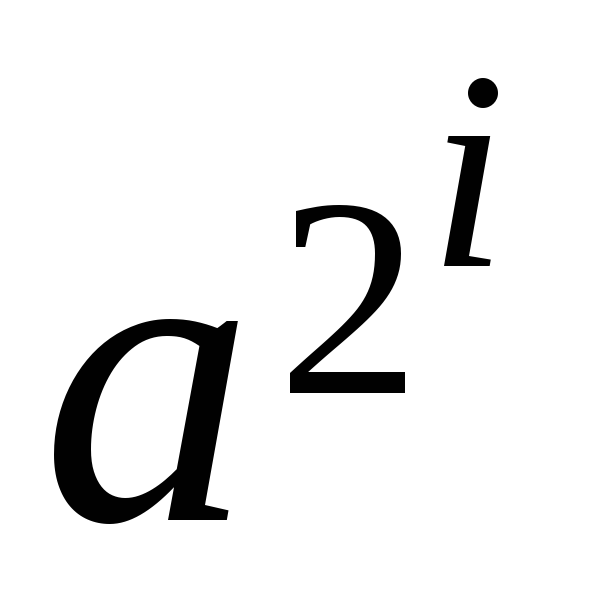 ,т.е.
в этом алгоритме (быстром!) не все степени
вычисляются, а из вычисленных не все
учитываются.
,т.е.
в этом алгоритме (быстром!) не все степени
вычисляются, а из вычисленных не все
учитываются.
p=1 а n |_2
a1 n0 | n|_2
a2 n1| n
. . . . . . .
p=p*![]()
![]() ,если ni
≠0
,если ni
≠0
. . . . . .
, nk-1 |n |_2
a2k nk | 0
Пример. Найтиa18.
18=100102, т.е.в произведении строятся степениa1,a2,a4,a8,a16,
а учитываются две, p=1*a2*a16
#include <iostream>
using namespace std;
// функция возведения a в степень n
double power (double a, int n)
{double p=1;
while (n!=1)
{if (n&1) p*=a; // анализ очередной двоичной цифры
a*=a; //в переменной a получается очередная степень
n>>=1; // сдвиг n
}
return p*a;
}
// Рекурсивный вариант функции возведения a в степень n
double powerR (double a, int n)
{if (n==0) return 1;
if (n==1) return a;
if (n&1) return powerR (a*a, n>>1)*a;
else return powerR (a*a, n>>1);
}
int main (){
cout<<power(2.0,18)<<endl;
cout<<powerR(2.0,18)<<endl;
return 0;
}
Результаты:
262144
262144
Представление вещественных чисел в памяти ПК
В С++есть два вещественных типа: float и double. Операции
вещественной арифметики выполняет сопроцессор (FPU).
Значение, полученное в сопроцессоре, преобразуется в тип float или double и хранится в этом типе.
Вещественное число представляется в виде (в IBM PC):
x=(-1)S * 1.f * 2p
Здесь S – знак(‘+’ - 0/’-’ - 1), 1.f – мантисса числа, p – порядок.
В памяти хранится: машинный порядок P’=P+д; д зависит от формата и кол-ва разрядов под порядок, 1 в целой части мантиссы в форматах float и double не хранится, но подразумевается, в сопроцессоре 1 в целой части мантиссы хранится.
|
S |
--- |
P’-> |
<- |
---- |
--f-- |
------ |
------ |
------ |
--- |
K
Под машинный порядок p’ отводится K разрядов: в эти к разрядов входит максимальное число max, д=max/2 , половина значений p’ соответствуют положительному истинному порядку p, половина отрицательному.P’ всегда положительный.
K=8 (float); K=11 (double); K=15(long double);
max=255 max=2047 max=32767
соответственно
д=127(float); д=1023(double); д=16383(long double);
p’= p+127 p’= p+1023 p’= p+16383
Для чисел X: 0< p’ <max;
Eсли P’=0 и f=0, то X=0.
Eсли P’=max, то данноеXне является числом, а представляет некоторое специальное значение:
+бесконечность : 0 11 . . .11 00. . . . 00
- бесконечность : 1 11 . . .11 00. . . . 00
P’ f
Не числа: (NaN, Not a Number):P’=11. . . 11, а f≠0
Неопределённость: P’=11. . . 11, а f=1000 . . . 00
Денормализованные числа: 0/1 P’=000. . . . 00, а f≠0
Положение точки не фиксируется, оно определяется порядком Pчисла, т.е. точка как бы плавает по разрядной сетке: для разных чисел её место может быть разным. Такая форма представления получила названиепредставления с плавающей точкой. Код числа в этом случае называют машинным кодом представления с плавающей точкой. Характеристики машинного слова: МС {n,k,m,q,E=2}, Е не хранится, оно выбирается при конструировании процессора, также как и способ представления порядкаP’.
В дальнейшем будем рассматривать тип double
Пример. X=3.5 = 11.12= (-1)0*1.11*21
P’ = 1+1023 =1024

 p’=1024f=0.11
p’=1024f=0.11
|
01000000 |
0000 |
1100 |
00000000 |
00000000 |
00000000 |
… |
00000000 |
7 6 5 4 3 0
16-ый код: 40 0С 00 00 00 00 00 00

