ЛАБОРАТОРНАЯ РАБОТА № 2 КОНСТРУКЦИЯ И РАСЧЕТ БОЛТОВЫХ СОЕДИНЕНИЙ

2.1 Цель работы

Изучение конструкций болтовых соединений и методики их расчета.

2.2 Оборудование и инструменты

Модели болтовых соединений, штангенциркуль, линейка.

2.3 Общие сведения

Болтовое соединение — одно из наиболее распространенных видов разъемного соединения. Простота изготовления и удобство сборки и разборки позволили использовать резьбу в большинстве деталей. Локомотивы, вагоны, подъемно-транспортные, строительные

ипутевые машины, стрелочные переводы, металлические конструкции содержат большое количество таких крепежных деталей, как болты, винты, шпильки, гайки, шайбы и другие.

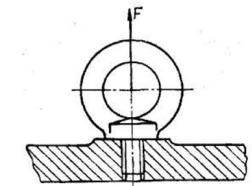
Примером незатянутого соединения одиночным болтом является нарезанный участок рым-болта (рис. 2.1), хвостовика крюков

идругие детали.

Рис. 2.1 Незатянутое соединение рым-болта

Опасным (расчетным) является сечение болта, ослабленное нарезкой. Площадь этого сечения оценивают приближенно по внутреннему диаметру резьбы d1,который находится из расчета на растяжение:

, (2.1)

где F— растягивающая сила, для рым-болта принимается равной весу редуктора G = тg(табл. 2.1);

— допускаемое напряжение,

Т , (2.2)

где σТ — предел текучести материала (табл. П. 5).

17

Марка резьбы принимается из табл. П. 6 так, чтобы ее внутренний диаметр d1был больше рассчитанного по формуле (2.1). Рекомендуется принимать рым-болты М8 и выше. Выбор оформляют по типу: «Принимаем рым-болт М8 ГОСТ 4751 -73».

Групповое болтовое соединение под нагрузкой, раскрывающей стык детали (рис. 2.2), нагружается в общем случае силой Q, направленной под углом α к оси х. Разложение силы Q на составляющие N и Sи ихприведение к центру тяжести стыка дает нагружение соединения двумя силами (отрывающей N и сдвигающей S) и опрокидывающим моментом М:

(2.3)

M NL1 SL2 .

Из условия нераскрытия стыка определяется напряжение смятия в стыке от затяжки:

, (2.4)

где — коэффициент запаса по нераскрытию стыка, =

1,3...2; — напряжение смятия от отрывающей силы; — напряжение смятия от момента.

(2.5)

(2.6)

В формулах (2.5) и (2.6) и — соответственно площадь и момент сопротивления стыка, т. е. основания стойки с размерами А и

В. При сплошном основании =АВ, a =АВ2/6. Усилие затяжки каждого болта из условия нераскрытия стыка:

, (2.7)

где z — число болтов соединения.

18

коэффициент трения, f= 0,3...0,35 для стали (чугуна) по бетону; f= 0,24 для стали (чугуна) по дереву; f=0,15..0,2 для стали по чугуну (стали).

При невыполнении условия (2.8) усилие затяжки определяется из условия сдвига:

. (2.9)

Расчетная нагрузка на болт

, (2.10)

где 1,3 — коэффициент, учитывающий касательные

напряжения, возникающие от момента трения в резьбе; — коэффициент внешней нагрузки, χ = 0,2...0,3; F— суммарная внешняя нагрузка:

. (2.11)

Внешняя нагрузка от силы N, приходящаяся на один болт

(2.12)

Внешняя нагрузка на наиболее нагруженные внешние болты в ряду 1 (рис.2.2):

k 1

где— число болтов в поперечном ряду, =2; lk =, и т.д. —

расстояния от оси симметрии плоскости стыка до осей болтов; k — число поперечных рядов с одной стороны от оси поворота; на рис. 2.2 k=2.

Рис. 2.2 Схема нагружения кронштейна

20

В соединении фундаментных болтов редуктора N = 0 и S = 0,a нагрузкой является только опрокидывающий момент М. Формула (2.4) примет вид:

Если редуктор крепится четырьмя болтами, то внешняя нагрузка от момента

FM = M/(2 l ),

где l — расстояние между осями болтов.

Опрокидывающий момент М определяется в зависимости от схемы редуктора и заданного момента на быстроходном валу T1. В двухступенчатом цилиндрическом редукторе (рис. 2.3)

М = |Т1-Т3|, (2.14)

где Т3 — реактивный крутящий момент со стороны исполнительного механизма на редуктор, направлен противоположно угловой скорости.

Рис.2.3 Крутящие моменты в двухступенчатом цилиндрическом редукторе

, (2.15)

где и — передаточные числа ступеней редуктора; — КПД одной зубчатой пары; = 0,95...0,97 [6].

Момент на промежуточном валу является внутренним и на корпус не передается. С учетом формул (2.14) и (2.15)

(2.16)

На рис.2.3 момент показан для двухступенчатого целендрического редуктора.

В коническо-цилиндрическом редукторе (рис. 2.4) моменты на быстроходном и тихоходном валах действуют в разных плоскостях.

21

обосновываются опасностью их разрушения при неквалифицированной затяжке. По той же причине не рекомендуется принимать болты меньше М8. Коэффициент запаса sможет быть определен по ориентировочно назначенному размеру болта из стали 20, для которой в табл. 2.3 приведены допускаемые нагрузки при неконтролируемой затяжке.

При несовпадении предварительно принятого размера и рассчитанного по формуле (2.19) коэффициент запаса корректируют и расчет повторяют.

Пример. Рассчитать диаметр болта из стали 35 при расчетной нагрузке Fp=20 кН.

Решение. Ориентируясь на болт М24 (табл. 2.3), принимаем методом линейной интерполяции s = 3.1 (табл. 2.2). Предел текучести стали 35 σТ = 300 МПа (табл. П. 5). Допускаемое напряжение

3003,1 96,8 .МПа Внутренней диаметр резьбы

.

Ближайший больший диаметр= 17,294 мм (табл. П. 6) соответствует резьбе М20. Принимаем резьбу М20 с s = 3,6 (или М22

с s = 3,4).

23