2. Вычисление нормальных напряжений и проверка прочности

Продольная сила является результирующей нормальныхнапряжений , которые распределены равномерно по поперечному сечению бруса, т. е. по (1.1) . Знак напряжениязависит от знака силы, а величина напряжения изменяется при изменении силы.

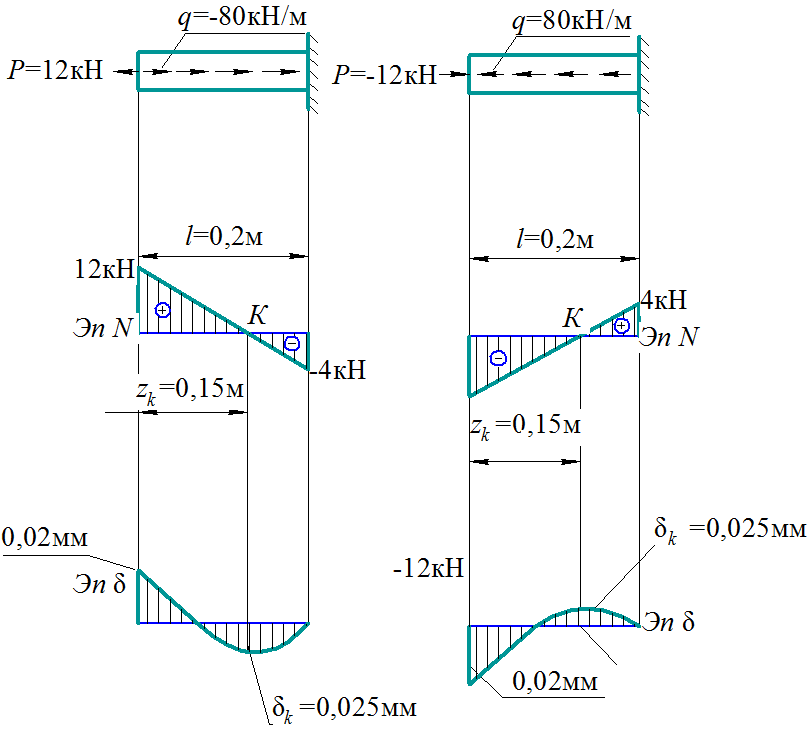
Для 1-го варианта значений Для 2-го варианта значений

а б

Рис. 2.2

1-й вариант

Требуемую проверку прочности (это проверочный расчёт) выполним, составив условие прочности по (2.3).

Сначала определим функцию по (1.1):

,

Найдём значения в начале и в конце бруса:

при ,

при .

Наибольшее напряжение по абсолютной величине оказалось равным

.

Подставив значения в (2.3), получаем

.

Отсюда делаем заключение: условие прочности выполняется.

Расчёт для 2-го варианта значений аналогичен.

3. Построение эпюры продольных перемещений и проверка жёсткости

В случае растяжения-сжатия бруса его поперечные сечения совершают поступательные перемещения, значения которых изменяются вдоль бруса. Для наглядности изменений строится эпюра перемещений ‒ график изменения перемещений вдоль оси бруса.

Для этого вычисляют перемещения некоторых характерных сечений и изображают под брусом на базисной линии (линии параллельной оси бруса) график изменения перемещений.

Далее по эпюре перемещений нужно установить значение наибольшего перемещения δ_max, и выполнить проверку жёсткости по (2.6).

1-й вариант

Вычислим абсолютную деформацию бруса Δl .

Можно подставить значения P, q и ЕА в окончательное выражение Δl (2.5). Но можно подстановку значений сделать в продольную силу N (2.2) и далее интегрировать по (2.4). Результат будет одинаков.

Например, выполним интегрирование, используя (2.4).

мм.

Далее определим перемещения двух характерных сечений: в начале и в конце бруса.

Для бруса с жёсткой заделкой удобно идти в расчётах от заделки, в которой перемещение равно 0:

.

Перемещение на свободном краю бруса запишем согласно (2.7):

мм.

Заметим, что эпюра N имеет линейный характер (рис. 2.2), но для наших значений в сечении К получено пересечение прямой N с базисной линией, т.е. для этого сечения продольная сила N_к=0. Тогда согласно выражению интеграла (2.5), в сечении К подынтегральная функция (это производная интеграла) равна 0, и поэтому здесь будет экстремум значения интеграла. Значит, в сечении К должен быть экстремум перемещения, и в этом сечении получим перегиб параболы перемещений.

В виду этого вычислим значение перемещения сечения К (перемещения δ_к) и уточним график перемещений.

Обозначим координату сечения К как z_к и вычислим значение экстремального перемещения δ_к. Так как продольная сила в сечении К

N_к = q∙z_к + P = 0,

то координата z_к м.

Перемещение δ_к фактически равно деформации куска бруса от заделки до сечения К.

Удобно сначала вычислить деформацию ∆l(z_к) куска бруса длиной z_к=0,15 м, отсчитывая от свободного края.

Значение ∆l(z_к) по (2.4) равно

Δl(z_к) ==

_.

Теперь через ∆l(z_к) запишем перемещение свободного края бруса δ, используя (2.7).

δ= δ_к + Δl(z_к).

Отсюда получаем искомое перемещение δ_к сечения К в виде

δ_к = δ - Δl(z_к) = δ - =

Проведём базисную линию (рис. 2.2), и перпендикулярно базисной линии отложим в выбранном масштабе полученные значения перемещений: на краю бруса вверх δ = 0,02мм; в сечении К вниз δ_К = -0,0025мм. Далее проводим параболу с перегибом для сечения К.

Проверим условие жёсткости.

Для этого из эпюры перемещений возьмём наибольшее перемещениемм и запишем по (2.6)

=0,5 мм,

значит, условие жёсткости выполняется.

Расчёт для 2-го варианта значений аналогичен.