2.Определение параметров уравнения линейной регрессии с помощью программы ms excel

Режим работы "Регрессия" служит для расчета параметров уравнения линейной регрессии и проверки его адекватности исследуемому процессу.

Для решения задачи регрессионного анализа в MS Excel выбираем в панели инструментов во вкладке Сервис команду Анализ данных и инструмент анализа "Регрессия".

В появившемся диалоговом окне задаем следующие параметры:

1. Входной интервал Y - это диапазон данных по результативному признаку. Он должен состоять из одного столбца.

2. Входной интервал X - это диапазон ячеек, содержащих значения факторов (независимых переменных). Число входных диапазонов (столбцов) должно быть аналогично диапазону Y.

3. Устанавливаем флажок «уровень надежности». Используется для проверки значимости коэффициента детерминации и коэффициентов регрессии.

4. В параметре «Выходной интервал» указать ячейку выходного диапазона.

5. Установить флажки в параметрах «остатки» и «стандартные остатки».

6. Остальные параметры оставляем по умолчанию.

После нажатия кнопки «ОК» в выходном диапазоне получаем результат.

Рекомендуемая литература

1. Головина Л.И. Линейная алгебра и некоторые ее приложения.- М.: Наука, 1995.

2. Кремер Н.Ш. Высшая математика для экономистов. М.: ЮНИТИ, 1998.

3. Дрейпер И., Смит Г. Прикладной регрессионный анализ: Пер. с англ. – Кн. 1,2 – М.: Финансы и статистика, 1986, 1987.

4. Крамер Г. Математические методы статистики: Пер. с англ. – М.: Мир 1975.

5 Кремер Н.Ш. Теория вероятностей и математическая статистика. – М.: ЮНИТИ, 2000

6. Кремер Н.Ш. Математическая статистика. = М.: Экономическое обозревание, 1992.

7. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютерах / Под ред. В.Э. Фигурнова. – Мю: Инфра-М. 1998.

8. Ферстер Э., Ренц Б. Методы корреляционного и регрессионного анализа: Пер. с нем. – М.: Финансы и статистика, 1982.

Приложение А

Пример выполнения расчетов по расчетно-графической работе

1. ИСХОДНЫЕ ДАННЫЕ

Таблица А1

Исходные данные

Переменная	Координаты
	первая	вторая	третья	четвертая	пятая
	3	5	7	11	6
	14	16	19	26	?

2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ ЛИНЕЙНОЙ РЕГРЕССИИ

Для начала необходимо определить суммы значений и(при этом пятую координату пока не учитываем), которые определяются как:

; .

Далее определим суммы значений и произведений

Вычислим коэффициенты линейной регрессии по формулам (3) и (4):

Составим искомое уравнение линейной регрессии вида (1):

3. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ДЕТЕРМИНАЦИИ

Перед тем как определить коэффициент детерминации произведем расчет.

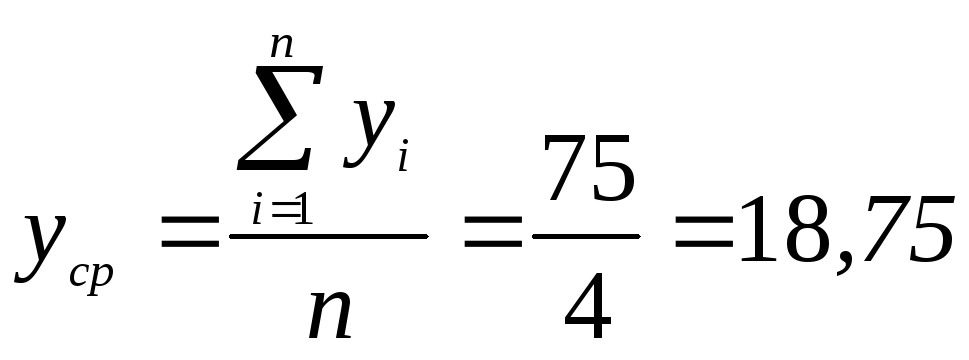
Далее определим значения ; объясненную вариациюи общую вариациюдля первой координаты:

Аналогично произведем расчет и для остальных координат, результаты расчетов сведем в таблицу А2

Таблица А2

Результаты расчетов объясненной и общей вариаций

Координата	Параметры
Первая	3	14	13,4	28,63	22,56
Вторая	5	16	16,46	5,26	7,56
Третья	7	19	19,52	0,56	0,06
Четвертая	11	26	25,63	47,35	52,56

Вычислим коэффициент детерминации по выражению (5):

или 99%

4. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ ЛИНЕЙНОЙ РЕГРЕССИИ В ПРОГРАММЕ MS EXCEL

Проведем регрессионный анализ с использованием режима «Регрессия» в программе MS Excel. Подготовка расчета представлена на рисунке А1, а результаты расчетов в таблицах А3-А5.

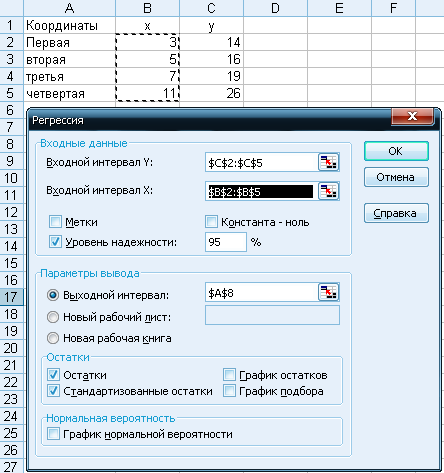
Рис. А1. Подготовка расчета в программе MS Excel

Таблица А3

Регрессионная статистика

Множественный R	R-квадрат	Нормированный R-квадрат	Стандартная ошибка	Наблюдения
0,99	0,98	0,98	0,7	4,000

Таблица А4

Параметры регрессии

Параметры	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	8,814286	0,841282	10,47721
Переменная X 1	1,528571	0,117803	12,97566

Таблица А5

Вывод остатка

Наблюдения	Предсказанное Y	Остатки	Стандартные остатки
1	13,4	0,6	1,054402535
2	16,45714286	-0,457142857	-0,803354312
3	19,51428571	-0,514285714	-0,903773601
4	25,62857143	0,371428571	0,652725379

Значения таблицы А4 показывают, что это уравнение, совпадает с уравнением, полученным при расчете по МНК вручную с точностью до ошибки округления.

В данном расчете коэффициент регрессии оказался положительным, следовательно, связь также является положительной.

Данные таблицы А5 показывают величину отклонения каждой точки от построенной линии регрессии. Наибольшее абсолютное значение остатка – 0,6, наименьшее - 0,37. Для наглядности построим график линейной регрессии, представленный на рисунке А2.

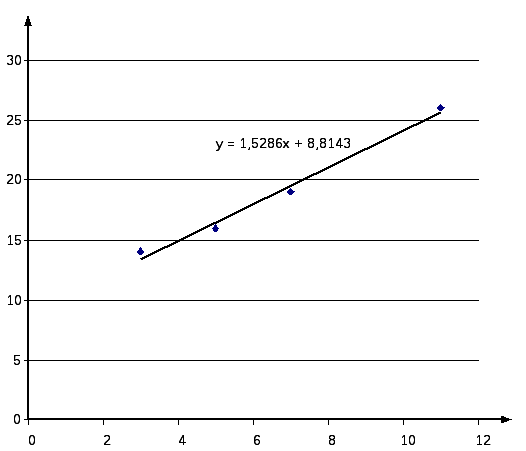
Рис. А1. График линейной регрессии для данного числового ряда

Поскольку коэффициент детерминации имеет достаточно высокое значение >100% следовательно, полученное уравнение линейной регрессии, возможно использовать для прогнозирования.

Определим параметр для пятой координаты: