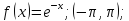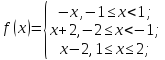12. Функцияналдық қатар

қатарының мүшелері x айнымалысына тәуелді болғандықтан функцияналды қатар деп аталады.

Функцияналдық қатар әртүрлі x мәндерінде әртүрлі жинақталатын не жинақталмайтын сандық қатарға айналады.

Функцияналдық қатар жинақталатын x мәндерінің жиынын осы қатардың жинақталу аралығы деп аталады.

Барлық функцияналды қатардың ең қарапайым әрі ең көп қолданылатын түрі келесі түрдегі дәрежелік қатар

немесе жалпы түрде

Функцияналдық қатардың жинақталу аралығын анықтау үшін әдетте алдымен Даламбер белгісін қолданамыз, сосын функцияналдық қатардың жинақталуы туралы сұрақ туындататын x мәндеріндегі сандық қатарды айрықша зерттейміз.

Мысал. Дәрежелік қатардың жинақтылық аралығын табыңыз.

Даламбер белгісін қолданып,

x-тің қандай мәндерінде бұл шек нөлден кіші болатынын анықтаймыз, яғни

теңсіздігін шешеміз.

Даламбер белгісі бойынша, осы интервалдағы x-тің кез келген мәндерінде қатар жинақталады (абсолютті), ал кезде жинақталмайды.

Интервалдың шектік нүктелерінде, яғни болғанда Даламбер белгісі жинақталуы жайлы сұраққа жауап бере алмайды. Сондықтан бұл нүктелерде ерекше зерттейміз.

болған кезде мүшелері оң болатын сандық қатарын аламыз. Бұл қатарды гармоникалық қатармен салыстырсақ жинақталатынын байқаймыз. (Зерттеп отырған қатарымыздың әрбір мүшесі гармоникалық қатардың мүшелерінен үлкен болады.)

болған кезде таңбалары кезекпе-кезек ауысатын сандық қатарын аламыз. Бұл қатар Лейбниц белгісі бойынша жинақталады. (Бұл қатардың мүшелері абсолютті шамасы бойынша кеміп, нөлге ұмтылады.)

Берілген дәрежелік қатардың жинақталу аралығына жартылай интервалы жатады.

Тапсырмалар:

Функцияналдық қатарларды жинақтылыққа зертте:

1.		2.
3.		4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.

13. Фурье қатары

мұнда тұрақтылар, осы функцияналдық қатарды тригонометриялық қатар деп атаймыз.

интервалында функциясына арналған Фурье қатары деп (1) түрдегі тригонометриялық қатарын атаймыз, егер оның коэффициенттері және клесі Фурье формулаларымен есептелінсе,

Функцияны Фурье қатарына жіктеудің ең қарапайым жеткілікті шартты келесі Дирихле теоремасында көрсетілген.

Егер интервалында функциясының бірінші текті үзілісті ақырлы нүктелері (не үзіліссіз болса) мен экстремум болатын ақырлы нүктелері (не мүлдем олар болмаса) бар болса, онда оның Фурье қатары жинақталады, яғни осы интервалдың барлық нүктелерінде қосындысы бар болса. Осыдан,

1. Үзіліссіз нүктелерде функциясы сол функцияның өзіне жинақталады,

2. Әрбір үзілісті нүктелерінде функциясы сол нүктелердегі функцияның оң жақты және сол жақты шектерінің қосындысының жартысына тең болады,

3. интервалының шектік нүктелерінде функциясы x нүктесі интервал ішінен шектік нүктелеріне ұмтылғанда

жұп функцияларына арналған барлық коэффициенттері болады және осыған сәйкес Фурье қатарында синустар болмайды.

Ал 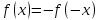тақ функцияларына арналған барлық коэффициенттері болады және осыған сәйкес Фурье қатарында тек қана синустар болады.

Мысал. интервалында функциясын Фурье қатарына жіктеңіз:

Алдымен берілген функция берілген аралықта Дирихле шартын қанағаттандыратындығын тексереміз; содан соң Фурье формуласымен және коэффициенттерін есептейміз және оларды (1) қатарға қойып, іздеп отырған берілген функцияның Фурье қатарына жіктеуін аламыз; соңында Дирихле теоремасына сүйене отырып x-тің қандай мәнінде алынған қатар берілген функцияға жинақталатындығын анықтаймыз.

Берілген функция тақта емес, жұпта емес болғандықтан, сондықтан (2) жалпы формула бойынша оның Фурье коэффициенттерін есептейміз. Функция аралығында берілгендіктен деп аламыз:

(Интегралды есептеу үшін бөліктеп интегралдау формуласы қолданылған.)

кезде кезде үшін алынған өрнектің мағынасы жоқ. Сондықтан коэффициентін жекеше деп алып (2) формула бойынша есептейміз:

1. тригонометриялық қатарға және коэффициенттерінің мәнін қоя отырып, ізделініп отырған берілген функцияның Фурье қатарына жіктелуін аламыз:

Бұл жіктеу орынды, яғни алынған қатар өзінің анықталу облысы-ның барлық нүктелерінде берілген функцияға жинақталады. ( және шектік нүктелерінде қатардың қосындысы тең, және де осы нүктелерде қатардың бірінші мүшесінен басқа барлық мүшесі нөлге ауысады. Сонымен қатар Дирихле теоремасы бойынша осы нүктелерде қатардың қосындысына ие болады.)

Тапсырмалар: берілген интервалында берілген функцияларды Фурье қатарына жіктеңіз:

1.		2.
3.		4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.