
- •Алғашқы функция және анықталмаған интеграл
- •Бөліктеп интегралдау
- •Рационал функцияларды интегралдау
- •Трансценденттік функцияларды интегралдау
- •Функция өсімше
- •Функцияның туындысы және дифференциалы
- •Тейлор формуласы
- •Доға ұзындығын есептеу
- •Көлемді есептеу
- •Қатарлардың жинақтылық белгісі
- •Таңбалары ауыспалы қатарлардың жинақтылық белгісі
- •Функцияналдық қатар
- •Фурье қатары
- •Фурье интегралы
- •Әдебиеттер тізімі
- •Қосымша
-
Доға ұзындығын есептеу
Егер
жазық кисық тікбұрышты координаттар
жүйесіне қатысты болып және
 немесе
немесе
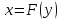 теулерімен
немесе
теулерімен
немесе
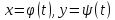 параметрлік
теңдеулерімен берілсе, онда оның
доғасының ұзындығының дифференциалы
параметрлік
теңдеулерімен берілсе, онда оның
доғасының ұзындығының дифференциалы
 келесі
формуламен беріледі:
келесі
формуламен беріледі:

Ал AB доғасының ұзындығы келесі формуламен анықталады:


Егер
жазық кисық тікбұрышты координаттар
жүйесіне қатысты болып және
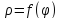 теңдеулері
берілсе, онда
теңдеулері
берілсе, онда


Мысал.
A(2;
-1) және
B(5;-8)
нүктелерінің
арасындағы
 жартыкубтық параболаның доғасының
ұзындығын есептеңіз.
жартыкубтық параболаның доғасының
ұзындығын есептеңіз.
Бұл теңдеуді y-ке қатысты шешеміз, сондықтан y’-ті табамыз:

(қисықтың
 таңбасы
Ox
өсіне симметриялы екенін көрсетеді;
қарама-қарсы
ординаттары бар A
және
B
түктелері
Ox
өсінен төмен орналасқан қисықтың
бөлігінде жатады.)
таңбасы
Ox
өсіне симметриялы екенін көрсетеді;
қарама-қарсы
ординаттары бар A
және
B
түктелері
Ox
өсінен төмен орналасқан қисықтың
бөлігінде жатады.)
Бұдан


Тапсырмалар:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
Ox
өсімен
қиылысу нүктелері арасындағы
|
|
8. |
|
|
9. |
|
|
10. |
|
-
Көлемді есептеу
xOy
жазықтығында
D
облысты
табаны бар және жоғарыдан
 бетімен
шектелген вертикаль цилиндрлі дененің
көлемі келесідей екілік интегралымен
өрнектеледі:
бетімен
шектелген вертикаль цилиндрлі дененің
көлемі келесідей екілік интегралымен
өрнектеледі:

Қиынырақ формадағы денелердің көлемін есептеу бірнеше вертикаль цилиндрлі денелердің көлемінің алгебралық қосындысын есептеуге келеді.
Мысал. Беттермен шектелген дененің көлемін есептеңіз:

Бұл
дене вертикаль цилиндр түрінде берілген.
Оны жоғарыдан
 жазықтығымен шектелген, ал төменнен
жазықтығымен шектелген, ал төменнен
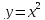 параболасы мен
параболасы мен
 түзуінің арасындағы xOy
жазықтығының
бөлігімен шектелген.
түзуінің арасындағы xOy
жазықтығының
бөлігімен шектелген.
Жоғарыдағы формулаға сәйкес бұл дененің көлемі келесідей болады:


Басқа ретпен интегралдаған кезде

Тапсырмалар:
Беттермен шектелген дененің көлемін есептеңіз:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
|
8. |
|
|
9. |
|
|
10. |
|

 циклоидының
бір аркасының доғасының ұзындығын
есептеңіз;
циклоидының
бір аркасының доғасының ұзындығын
есептеңіз; қисығының
доғасының ұзындығын есептеңіз;
қисығының
доғасының ұзындығын есептеңіз; эллипс
эволютының доғасының ұзындығын
есептеңіз;
эллипс
эволютының доғасының ұзындығын
есептеңіз; Архимед
спиралының бірінші түйінінің доғасының
ұзындығын есептеңіз;
Архимед
спиралының бірінші түйінінің доғасының
ұзындығын есептеңіз; кардиоидының
доғасының ұзындығын есептеңіз;
кардиоидының
доғасының ұзындығын есептеңіз; және
және
 түзулері
арасындағы
түзулері
арасындағы
 қисығының
доғасының ұзындығын есептеңіз;
қисығының
доғасының ұзындығын есептеңіз; қисығының доғасының ұзындығын
есептеңіз;
қисығының доғасының ұзындығын
есептеңіз; және
және
 түзулері арасындағы
түзулері арасындағы
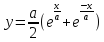 тізбекті сызығының доғасының ұзындығын
есептеңіз;
тізбекті сызығының доғасының ұзындығын
есептеңіз; астроидының
доғасының ұзындығын есептеңіз;
астроидының
доғасының ұзындығын есептеңіз;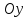 өсімен
қиылысу нүктелері арасындағы
өсімен
қиылысу нүктелері арасындағы
 қисығының доғасының ұзындығын
есептеңіз;
қисығының доғасының ұзындығын
есептеңіз;


 конуспен
және
конуспен
және
 цилиндрмен және
цилиндрмен және
 жазықтықпен берілген.
жазықтықпен берілген. жазықтығымен
және
жазықтығымен
және
 цилиндрмен берілген.
цилиндрмен берілген. сферамен
және
сферамен
және
 цилиндрмен
берілген.
цилиндрмен
берілген.
 жазықтықтармен
және
жазықтықтармен
және
 цилиндрмен
берілген.
цилиндрмен
берілген. эллиптикалық
параболоидтармен және
эллиптикалық
параболоидтармен және
 жазықтықтармен
берілген.
жазықтықтармен
берілген.
 жазықтықтармен
берілген.
жазықтықтармен
берілген. цилиндрімен
және
цилиндрімен
және
 жазықтықтарымен берілген.
жазықтықтарымен берілген.