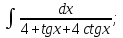- •Алғашқы функция және анықталмаған интеграл
- •Бөліктеп интегралдау
- •Рационал функцияларды интегралдау
- •Трансценденттік функцияларды интегралдау
- •Функция өсімше
- •Функцияның туындысы және дифференциалы
- •Тейлор формуласы
- •Доға ұзындығын есептеу
- •Көлемді есептеу
- •Қатарлардың жинақтылық белгісі
- •Таңбалары ауыспалы қатарлардың жинақтылық белгісі
- •Функцияналдық қатар
- •Фурье қатары
- •Фурье интегралы
- •Әдебиеттер тізімі
- •Қосымша
-
Трансценденттік функцияларды интегралдау
Трансценденттік рационал функцияларды интегралдау келесі түрдегі интегралдарды есептеуге келеді, мұнда R –рационал функция:
-
 мұндай
түрдегі интегралдарды интегралдау
үшін
мұндай
түрдегі интегралдарды интегралдау
үшін
 алмастыру енгіземіз. Сонымен қатар,
алмастыру енгіземіз. Сонымен қатар,
 ,
,
 ,
,
 .
.
-
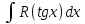 ,
мұнда
,
мұнда
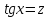 алмастыруын енгіземіз. Сонымен қатар,
алмастыруын енгіземіз. Сонымен қатар,
 .
. -
 мұнда
мұнда
 алмастыруын
енгіземіз. Сонымен қатар,
алмастыруын
енгіземіз. Сонымен қатар,
 .
.
Мысал.

 деп
алып, жоғарыдағы алмастыруларды
енгіземіз.
деп
алып, жоғарыдағы алмастыруларды
енгіземіз.


Тапсырмалар:
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
16. |
|
|
17. |
|
18. |
|
|
19. |
|
20. |
|
|
21. |
|
22. |
|
|
23. |
|
24. |
|
|
25. |
|
|
|
-
Функция өсімше
 функциясы
берілсін. Мұндағы,
х
– тәуелсіз айнымалы (аргумент), у
–
тәуелді айнымалы (функция).
функциясы
берілсін. Мұндағы,
х
– тәуелсіз айнымалы (аргумент), у
–
тәуелді айнымалы (функция).



Мысал
1.
 функцияның
өсімшесін табыңыз.
функцияның
өсімшесін табыңыз.


Мысал
2. функцияның
өсімшесін табыңыз.
функцияның
өсімшесін табыңыз.

Анықтама.
 функциясының
туындысы деп
функциясының
туындысы деп
 ұмтылған
кезде
осы
функцияның
ұмтылған
кезде
осы
функцияның
 өсімшесі
сәйкесінше
тәуелсіз айнымалының
өсімшесі
сәйкесінше
тәуелсіз айнымалының
 өсімшесіне қатынасының шегін айтамыз:
өсімшесіне қатынасының шегін айтамыз:

Туынды
келесідей белгіленеді:
 немесе
немесе
 немесе
немесе
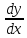 .
.
Туынды табу амалы дифференциалдау деп аталады.
Көптеген жерде туынды табу формулалары беріледі, бұл әдістемелік құралда сол элементар функциялардың туындысын табу жолын келтірейік:
-
 тұрақтының
туындысын табу жолы:
тұрақтының
туындысын табу жолы:


-
 туындысын
табу жолы:
туындысын
табу жолы:



-
 модулді
функцияның туындысын табу жолы:
модулді
функцияның туындысын табу жолы:

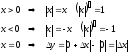
 шегі
анықталмайды. Демек,
шегі
анықталмайды. Демек,

-
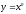 дәрежелік
функцияның туындысын табу жолы:
дәрежелік
функцияның туындысын табу жолы:



-
 көрсеткіштік
функцияның туындысын табу жолы:
көрсеткіштік
функцияның туындысын табу жолы:



-
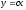 туындысын
табу жолы:
туындысын
табу жолы:




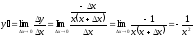
-
 туындысын
табу жолы:
туындысын
табу жолы:


-
 туындысын
табу жолы:
туындысын
табу жолы:




-
 туындысын
табу жолы:
туындысын
табу жолы:


-
 тригонометриялық
функцияның туындысын табу жолы:
тригонометриялық
функцияның туындысын табу жолы:

 себебі,
тамаша шек бойынша
себебі,
тамаша шек бойынша



себебі,
тамаша шек бойынша



Себебі,
тамаша шек бойынша

 себебі,
тамаша шек бойынша
себебі,
тамаша шек бойынша











Тапсырмалар:
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
16. |
|
|
17. |
|
18. |
|
|
19. |
|
20. |
|
|
21. |
|
22. |
|
|
23. |
|
24. |
|
|
25. |
|
|
|