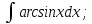- •Алғашқы функция және анықталмаған интеграл
- •Бөліктеп интегралдау
- •Рационал функцияларды интегралдау
- •Трансценденттік функцияларды интегралдау
- •Функция өсімше
- •Функцияның туындысы және дифференциалы
- •Тейлор формуласы
- •Доға ұзындығын есептеу
- •Көлемді есептеу
- •Қатарлардың жинақтылық белгісі
- •Таңбалары ауыспалы қатарлардың жинақтылық белгісі
- •Функцияналдық қатар
- •Фурье қатары
- •Фурье интегралы
- •Әдебиеттер тізімі
- •Қосымша
-
Алғашқы функция және анықталмаған интеграл
Өзінің
дифференциалына қарап
 функциясын іздеу, яғни дифференциалдауға
кері амалын интегралдау деп атаймыз,
ал ізделінді
функциясын іздеу, яғни дифференциалдауға
кері амалын интегралдау деп атаймыз,
ал ізделінді
 функциясын
функциясын
 функциясының алғашқы функциясы деп
аталынады.
функциясының алғашқы функциясы деп
аталынады.
Кез
келген үзіліссіз
 функциясының бір-бірінен тек тұрақты
санға ғана ерекшеленетін көптеген
әртүрлі алғашқы функциялары бар болады.
Егер
функциясының бір-бірінен тек тұрақты
санға ғана ерекшеленетін көптеген
әртүрлі алғашқы функциялары бар болады.
Егер
 функциясы
функциясы
 функциясының алғашқы функциясы болса,
яғни егер
функциясының алғашқы функциясы болса,
яғни егер
 болса, онда
болса, онда
 да алғашқы функция болады, мұнда
да алғашқы функция болады, мұнда
 -кез
келген тұрақты сан. Немесе
-кез
келген тұрақты сан. Немесе
 болады.
болады.
 функциясының
барлық алғашқы функцияларының жиыны
жалпы
функциясының
барлық алғашқы функцияларының жиыны
жалпы
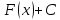 өрнегі осы функцияның анықталмаған
интегралы деп аталады және
өрнегі осы функцияның анықталмаған
интегралы деп аталады және
 белгісімен
белгіленеді:
белгісімен
белгіленеді:

Анықталмаған интегралдардың кейбір қасиеттері.
-

-

-
 яғни
тұрақты көбейткішті интеграл белгісінің
алдына шығаруға болады.
яғни
тұрақты көбейткішті интеграл белгісінің
алдына шығаруға болады. -
 яғни
қосындылардың интегралы барлық
қосылғыштардың интегралдарының
қосындысына тең.
яғни
қосындылардың интегралы барлық
қосылғыштардың интегралдарының
қосындысына тең.
Интегралдаудың негізгі формулалары:
Мысал.

Шешуі:
 =
= ;
;
Тексеру: туындысын алып, функцияның дұрыс интегралданғанын тексереміз.

Мысал.
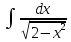 ;
;
Шешуі:

10-ші формуланы қолданып шығардық.
Тексеру:


Мысал.

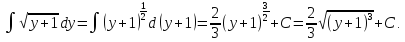
Тексеру:

Тапсырмалар:
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
16. |
|
|
17. |
|
18. |
|
|
19. |
|
20. |
|
|
21. |
|
22. |
|
|
23. |
|
24. |
|
|
25. |
|
|
|
-
Бөліктеп интегралдау
 осы
көбейтудің
дифференциалының формуласын екі жағын
интегралдап, келесі бөліктеп
интегралдау формуласын
аламыз:
осы
көбейтудің
дифференциалының формуласын екі жағын
интегралдап, келесі бөліктеп
интегралдау формуласын
аламыз:

Бұл
формулада
 интегралын зерттеуде мына
интегралын зерттеуде мына
 интегралды есептеуге келеді. Мұнда
бастапқы интегралды есептеу соңғы
интегралды есептеуден қиынырақ
болғандықтан осы формуланы пайдаланып
шығарамыз.
интегралды есептеуге келеді. Мұнда
бастапқы интегралды есептеу соңғы
интегралды есептеуден қиынырақ
болғандықтан осы формуланы пайдаланып
шығарамыз.
 интегралын
есептеу үшін интеграл астындағы өрнекті
u
және
dv
деп
белгілеп алу керек. dv
ретінде
көбінесе туынды алынбайтын функцияларды
аламыз, мысалы үшін
интегралын
есептеу үшін интеграл астындағы өрнекті
u
және
dv
деп
белгілеп алу керек. dv
ретінде
көбінесе туынды алынбайтын функцияларды
аламыз, мысалы үшін
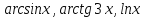 .
.
Мысал.


Тапсырмалар:
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
16. |
|
|
17. |
|
18. |
|
|
19. |
|
20. |
|
|
21. |
|
22. |
|
|
23. |
|
24. |
|
|
25. |
|
|
|


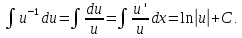















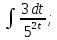








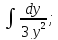

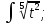
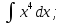
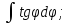




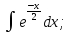















 ;
;