ЛАБ MAPLE ИС / ЛАБ 7-1 секущая и касательная

3

ЛАБОРАТОРНАЯ РАБОТА № 7-1

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Производная непрерывной функции является одной из важнейших её характеристик. Она используется в задаче исследования поведения функции, построения её графика, в задачах условной и безусловной оптимизации и многих других. Производная непрерывной функции одной переменной в заданной точке x определяется как предел отношения её приращения к приращению аргумента при стремлении последнего к нулю:

Для вычисления производных в Maple существует специальная команда diff(), которая позволяет вычислять как производные любых порядков функций одной переменной, так и частные производные функций многих переменных.

Геометрический смысл производной. Касательная к графику функции

Начнем раздел с демонстрации геометрического смысла производной как тангенса угла наклона касательной к графику функции в заданной точке. Касательная определяется как предельное положение секущей, проходящей через две точки графика при стремлении одной из них к другой. Все построения осуществим на примере функции:

.

Будем вычислять производную в точке x₀=1. Для этого зададим саму функцию и две точки её графика с абсциссами, соответственно, x₀=1 и x₁= x₀+h:

> y:=x->(exp(cos(x))+3)^2;

> x0:=1;

> p0:=[x0, y(x0)];

> p1:=[x0+h, y(x0+h)];

Команда slope() (наклон) из пакета student вычисляет тангенс угла наклона прямой, проходящей через две заданные точки:

> with(student): t:=slope(p0,p1);

Теперь, если устремить h к нулю, то выражение t должно сходиться к числу, равному тангенсу угла наклона секущей в предельном положении, т.е. тангенсу угла наклона касательной к графику функции в точке x=1. Зададим последовательность значений h_values, сходящуюся к нулю: , и посмотрим, к чему будет сходиться последовательность значений, определяемых выражением t:

> h_values:=seq(2/i^3,i=1..15);

> seq(evalf(t), h=h_values);

-5.439033250, -12.57034624, -13.3498521, -13.5137879, -13.569058,

-13.592932, -13.604946, -13.611648, -13.615686, -13.61826,

-13.61998, -13.62116, -13.62203, -13.62266, -13.62313

Видно, что эта последовательность сходится, и очень быстро. Но сходится ли она к значению производной функции в точке x=1? Вычислим производную с помощью функции diff():

> evalf(eval(diff(y(x),x),x=1));

Команда eval служит для подстановки числовых значений в функцию. Команда evalf – для вычисления приближённого значения выражения.

Замечаем, что построенная нами последовательность сходится к значению производной в точке x=1. Уже ее пятнадцатый член имеет два точных знака после запятой. Точный результат получим, если вычислим предел выражения t при h0:

> limit(t,h=0);

> evalf(%);

Графические возможности Maple позволяют увидеть, как секущая приближается к касательной. Построим уравнение секущей как прямой, проходящей через две заданные точки с координатами (x0, y(x0)) и (x0+h, y(x0+h)) соответственно (здесь Y является зависимой, а X независимой переменными):

> (Y-y(x0))/(y(x0+h)-y(x0))=(X-x0)/((x0+h)-x0);

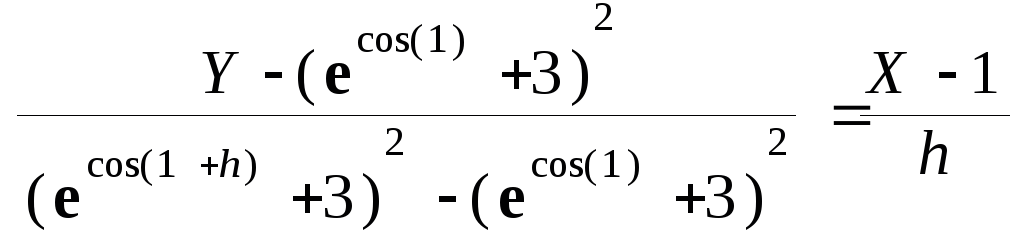
Выразим зависимую переменную Y через независимую X и представим в виде функции:

> isolate(%,Y);

> line_sec:=unapply(rhs(%),X);

Команда unapply преобразует выражение в функцию. Команда rhs означает “right hand side” – правая часть выражения. % означает результат предыдущей операции. Мы получили уравнение секущей.

Аналогично построим в виде функции уравнение касательной. Здесь используется известное уравнение касательной.

> line_tang:=X->eval(diff(y(x),x),x=1)*(X-x0)+y(x0);

Теперь можем построить последовательность изображений, содержащих график функции, её касательной и секущей при изменении параметра h, и отобразить её в виде анимационной картинки командой display():

> S:=seq( plot([y(x), line_tang(x), line_sec(x)], x=0..4,

view=[0..3,10..40], color=[black,black,green], thickness=2),

h=h_values):

> with(plots): display(S,insequence=true);

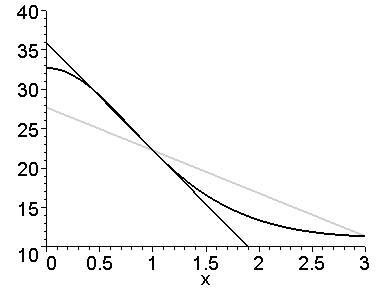
Параметр insequence означает, что графики будут показаны в последовательности. При покадровом просмотре анимации секущая будет изменять свое положение, приближаясь к касательной и, в конце концов, сливаясь с ней.

ЗАДАНИЕ 1. Решите те же задачи, задав другие последовательности h_values Секущая будет медленнее стремиться к касательной, если или . При этом секущая не доходит до касательной, поэтому следует увеличить число членов последовательности до 50 и более.

ЗАДАНИЕ 2. Исследуйте приближение секущей к касательной для функции в точке . График стройте в диапазоне [-1, 1] по х и у.