1. 5. Описание алгоритма логической последовательности выполнения команд пс в условиях разрушения множества q
Шаг 1.В соответствии с троичной организацией систем различной физической природы необходимо осуществить троичную организацию исполнения команд ПС.
Шаг
2.Для реализации каждой основной
команды наi-ом шаге
(ЦПС
«А»)
формируются последовательно две команды,
соответственно ЗПС
«А»
и ОПС
«А».
Шаг 3. Выделяется дополнительно три ячейки в свободном поле памяти.
Шаг
4.Наi-ом шаге логической
последовательности команд после
выполнения основной команды (ЦПС
«А»)
выполнятся команда контроля:
- состояний трёх ячеек i+1-го шага (например, по контрольной сумме содержимого),
- исходящего адреса, передавшего управление на i+1-ый шаг,
- адрес передачи управления на i+1-ом шаге.
Шаг
5.Если контроль прошел успешно, то
выполняется основная команда наi+1ом
ша ге (ЦПС
«А»).
Шаг 6.Если контроль прошел не успешно (обнаружено изменение содержимого хотя бы одной из трех ячеекi+1-го шага выполнения программы) осуществляется
6.1.если эталон храниться в специальном разделе памяти, то передача управления из 3-ей ячейкиi+1-го шага в ОС с запросом эталонного содержимого тройки ячеекi+1-го шага;
6.2.
если эталон храниться в специальном
упакованном формате в поле размещения
ЗПС
«А»
и ЗПС
«А»i-го шага.
Шаг 7.Эталонное содержимое тройки ячеекi+1-го шага, размещённое в вариантах 6.1. или 6.2. реализуется на резервном поле памяти с возвратом наi+2-й шаг и последующим предварительным контролем содержимого тройки ячеекi+2-го шага и т.д.
ППЭ
соответствующих подсистем («подпроцессоров»)
сторон обозначим следующим образом:
-
ППЭ ЦПС"А"("Б");
-
ППЭ ЗПС"А"("Б");
-
ППЭ ОПСА"("Б").
Множество
Qсостоит из занумерованных
непересекающихся фрагментовQ
.Q
-
это тройка команд, соответственно,
состоящая из
- основной команды;
- команды контроля состояния последующей требуемой тройки команд (эта команда блокирует действие ЦПС противника т.е. изолирует соответствующий изменённый фрагмент памяти (в котором размещена последующая требуемая тройка команд) с последующим уничтожением результатов действия противника, очищением соответствующего фрагмента памяти);
- команды реализующей требуемую последующую команду в новых, измененных состояниях программно-аппаратной среды и возвращающую логика выполнения команд в прежнюю последовательность.
С
другой стороны Q
-
это функция – правило (комбинатор лямбда
- исчисления) которое преобразует
определённое количество требуемых
символов в памяти ЭВМ. При этом надо
понимать, что соответствующие комбинации
символов (также это функции-правила)
однозначно связаны и воздействуют, как
на внешнюю память, так и на другие внешние
устройства.
Мы
рассмотрели условия функционирования
ПС в условиях разрушения программно-аппаратной
среды при предположении бессбойной
работы процессора. Для распространения
в модели учета закона сохранения
целостностинеобходимо перейти от
схемы «машины фон Неймана» к ЭВМ с
многомерно организованной памятью и
соответственно многомерными командами.
Допустим, не нарушая общности, что в
нашем случае ЭВМ имеет трёхмерную
память. То есть ПВС ЭВМ есть декартово
произведениеR=X×Y×Z×Т,
где памятиX,Y,Z
-соответствующие линейные фрагменты
многомерной памяти∏=X×Y×Z,
а Тдлительность работы ЭВМ.Р
,
Р
,
Р
- соответствующие процессоры, работающие,
как в своей, так и в остальных двух
линейных фрагментах многомерной памяти.
Каждая команда реализуется одновременно
на трёх процессорах и в соответствующих
линейных фрагментах многомерной памяти.
Поэтому, если обратиться к основному
соотношению
(u(r),v(r),r)dr
= I(Q),
то видно, что если даже будут разрушены
два процессора, команды всё равно будут
реализовываться на оставшемся исправном
процессоре.
С
другой стороны Q
-
семантически несёт в себе функции –
правила (комбинатор лямбда - исчисления)
которые преобразуют определённое
количество требуемых символов в памяти
ЭВМ. При этом надо понимать, что
соответствующие комбинации символов
(также это функции-правила) однозначно
связаны и воздействуют, как на внешнюю
память, так и на другие внешние устройства.
В таблице 5.1. представлены отношения ППЭ ЦПС"А" и ППЭ перечисленных подсистем противостоящих сторон "А" и "Б". В таблице 5.2. в первой строке и первом столбце представлены ППЭ соответствующих подсистем, а на пересечении представлены отношения (результирующие ППЭ) соответствующих подсистем сторон.
-
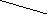АБ
(r)
(r)
(r)
(r)F
(
,
)F
(
,
,
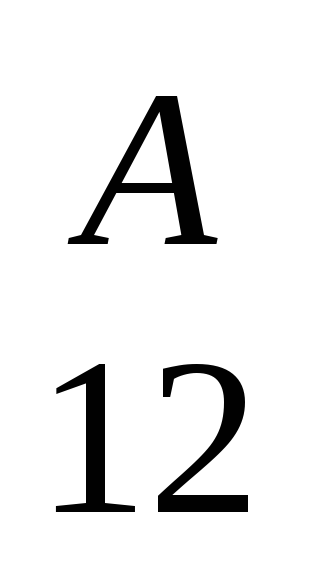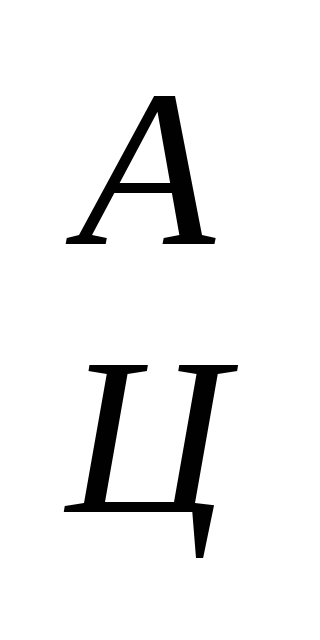)F
(
,
,
)
(r)F
(
,
)F
(
,
)F
(
,
,
)
(r)F
(
,
)F
(
,
,
)F
(
,
,
)
Таблица 5.1. Матрица отношенийППЭподсистем для "А"
-
АБ
(r)
(r)
(r)
(r)F
(
,
)F
(
,
)F
(
,
)
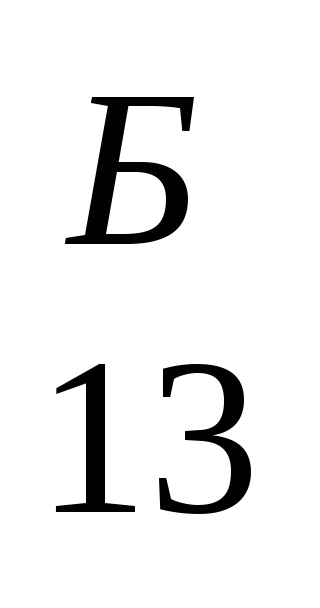(r)F
(
,
,
)F
(
,
)F
(
,
,
)
(r)F
(
,
,
)F
(
,
,
)F
(
,
,
)
Таблица 5.2. Матрица отношений ППЭ подсистем для "Б"
Физически
ППЭ каждой из трёх подсистем это
производительность, распределённая в
пространстве и времени. Обобщённый ППЭ
в общем случае есть определённая
комбинация соответствующих функций
(пространства и времени) – производительностей
соответствующих подсистем (Для стороны
«А»: 
(r),
(r),
(r);
для стороны «Б»: 
(r),
(r)
(r)).
Гдеr ∊Q⊂R=X×T.
Так
например элемент F
характеризует ППЭ ЦПС"А" в условиях
применения на совместном множестве ЦПС
"Б". F
характеризует ППЭ ЦПС"А" в условиях
применения на совместном множестве ЦПС
"Б" и противодействия этой подсистеме
ЗПС"А". F
(...)
= F
(...),
так как ОПС"А" не предназначена
для борьбы с ЦПС"Б".F
(...)
=F
(...)
=F
(...)
=
(r).
При этом F
(...)=
(r) в силу того, что в перечень задач ОПС
"Б" не входятзадачипротивостояния
ЦПС"А". F
(...)
=
(r)
в силу того, что по своему целевому
предназначению в перечень задач для
ЗПС"А" и ОПС"Б" не входит задача
противостояния ЦПС"А". Аналогично
рассуждая можно проанализировать
матрицу отношений ППЭ для стороны "Б".
Рассмотрев отношения ППЭ сторон проведем аналогичные исследования с РСОУ (Q) соответствующих подсистем. В таблице 5.3. представлена матрица отношений множеств требуемых ПВС подсистем.
|
Б |
Q |
Q |
Q |
|
Q |
O |
O |
O |
|
Q |
O |
O |
O |
|
Q |
O |
O |
O |
А
Отношение
РСОУ противо- стоящих сторон
характеризу-ется специальной мерой
O
=(Q
∩Q
),
где, i - 1(1)3 есть номера столбцов матрицы
(Таб.4.3.), j-1(1)3 есть номера строк матрицы
(Таб.4.3.),- мера
множества пересечения РСОУ соответствующих
под- систем сторон. Мера пересече- ния
РСОУ соответствующих подсистем определяет
степень соприкосновения противостоящих
подсистем. На множестве пересечений
РСОУ формируются отношения ППЭ, суть
элементов матрицы Таб.5.1.-5.2. А на основе
выявленных отношений ППЭ на множествах
пересечений РСОУ формируется специальное
множество и обобщенный ППЭ своими
свойствами удовлетворяющие требованиям
достижения соответствующими подсистемами
заданных уровней ЭП. Физически обобщённые
ППЭ являются в каждой точке пространства
функцией специальной комбинации трёх
производительностей (интенсивностей
деятельности) соответствующих подсистем
соответствующих сторон. В случае
компьютерных технологий это комбинации
интенсивностей преобразования символов
в памяти ЭВМ.
Для получения количественных характеристик необходимо решить 2 класса задач.
ЗАДАЧИ синтеза облика системы и способов применения.
1.Решить систему NMH интегральных уравнений Вольтерра 1-го рода
Для
стороны "*"
K
(t
,
t)
(t)dt
=I
(t
),
(*=А,Б) с ограничением
I
(t
)
= I
и
операторной связью, характеризующей
отношения ППЭ конфликтующих сторон
(·)=c
(p
(·),p
(·),
(·),
(·),
(·),
(·),
(·),
(·),W
,W
,Q
,Q
,Y
,Y
),
(Д)
где
- интенсивности функционирования,
соответственно, ЦПС(*), ЗПС(*), ОПС(*) вX
области
пространства X; W ,Q Y - ресурсы, соответственно,
ЦПС(*), ЗПС(*),ОПС.(*); p
-
вектор - функция вероятностей состояний
подсистем (например, решает - не решает
поставленную задачу) а ядро уравнения
сформировано из операторов, отображающих
множества ПВС и характеристики подсистем
систем, ресурсов, количественного
состава на числовое множество. При
значении ядра равного единице
обеспечивается требуемое размещение
элементов системы (производительности)
в пространстве. При моделировании
вычислительных процессов осуществляется
виртуальное перемещение процессоров
по памяти.
2. Решить систему N*M*H вариационных задач в форме Лагранжа
для
стороны "*"
K
(t
,t)
(t)dt
;
(* =А,Б)
с
ограничением
I
=I
и операторной связью (Д).
В рамках разработанной схемы разрешения конфликта необходимо определить условия устойчивости ситуации. При устойчивой ситуации сдерживание обеспечивается и обратно. Критерием является показатель ЭП ЦПС. Необходимо оценить способность системы решать поставленные задачи в условиях меняющейся обстановки. Для этого введено понятие устойчивость действий. При этом надо понимать, что это свойство процесса носит двойственный характер. На этапе определения научно - технической политики это свойство потенциальное. На этапе применения эта характеристика уже принимает реальное воплощение в системе.
Определение. 5.1. Устойчивость целенаправленных действий - комплексная характеристика, определяющая способность системы, в процессе целенаправленных действий (ЦД) достигать требуемого уровня ЭП.
Понятие устойчивость целенаправленных действий является предметом исследования теории структурной устойчивости. Если ситуация неустойчива в смысле действий, то стороны корректируют научно-технические программы в интересах повышения ЭП и соответственно устойчивости действий. Для этого определены условия устойчивости действий.
Теорема
5.1.Если допустимые вариации
производительности системы удовлетворяют
условию 
(t)dta
,то для того,чтобы ЦД были устойчивы
в окрестности(I
-
a
) I
(I
+
a
)необходимо и достаточно, чтобы вариации
вектора управления u(t) и вектора
возможностей v(t) удовлетворяли
условию
grad
K
(t
,
t)
u
(t)
+ grad K
(t
,
t)
v
(t)dt
a
.
УЧЕТ ФАКТОРОВ НЕОПРЕДЕЛЕННОСТИ. Задача решена в классе кусочно - программных управлений (КПУ),
Суть КПУ для стороны "А": Пара {s,а}, где s - разбиение множества
Т=
(t
t
...t
),
а: X
U
L
[t
,
t
]
;
Суть
КПУ для стороны "Б": Пара {s,в}, где
s – разбиение множества T =(t
t
...t
)
в:
X
U
L
[t
,
t
]
Суть операторов "а" и "в":
1.
Решается задача программного управления
с граничными условиями X
(t
),
X
(t
)
и формируются u
(t)
при t[t
,
t
]
2.
Выделяется u
(t)U
L
[t
,
t
]
;
3.
Если t
<
t
,
то переход к п.1 , иначе задача решена.
В случае решения Задачи Б. получены условия существования ситуации ""- равновесия (гдеесть мера неопределенности информации об участниках).
=
+
;
,
-
мера неопределенности о сторонах А,Б;
В классе КПУ имеют место следующие соотношения:
1)
I(u
(·),
u
(·))
+
I(u
(·),
u
(·))
I(u
(·),
u
(·))
- ;
2)
[
I(u
(·),
u
(·))]
= I(u
(·),
u
(·)).
Результат инвариантен к форме реализации меры неопределенности.
Компоненты векторов возможностей и управления и их отношения характеризуют модель системы. Такой подход к разработке системы позволяет достаточно полно для практики отразить основную сущность процесса функционирования системы и осуществить синтез:
Для случая противостояния "А" и "Б" вектор ПВС определяется следующим образом.
q
=〈x
,t
〉
=θ
((U
,V
,u
(r),v
(r)),(U
,V
,u
(r),v
(r))),
q
=〈x
,t
〉
=θ
((U
,V
,u
(r),v
(r)),(U
,V
,u
(r),v
(r))).
Тогда
решение задачи синтеза при заданном
множестве G сведется к отысканию
экстремумов
ЗАДАЧА
С1. extr I
((U
,V
,u
(
r ),v
(
r )),(U
,V
,u
(
r ),v
(
r )));
extr
I
((
U
,V
,u
(
r ),v
(
r )),(U
,V
,u
(
r ),v
(
r ))).
Решение задачи синтеза при нефиксированном множестве G и заданных U, V сторон сведется к отысканию экстремумов
ЗАДАЧА
С2. extr I
(
G
,G
),
extr I
(
G
,G
).