4.5.3. Сортировка методом выбора из дерева

Аналогом этого метода являются спортивные соревнования по олимпийской системе, то есть с выбыванием проигравших.

Пусть количество сортируемых элементов является степенью двойки: .Построение дерева сортировки начинается снизу, с листьев, которые содержат все элементы массива. Выбираются максимальные ключи в непересекающихся парах соседних элементов

.

Обозначим их через . Они становятся корнями соответствующих пар. Эти «победители» снова разбиваются на пары,

,

из которых выбираются максимальные ключи и делаются корнями для соответствующих пар, и т. д. Первый этап завершается, когда на-м шаге из двух оставшихся претендентоввыбирается элементс абсолютно максимальным значением ключа. Индексзапоминается в качестве первого элемента упорядоченного списка (рис. 24).

После этого лист заменяется на, так что теперь повторение всей процедуры даст элемент со вторым по величине значением ключа (рис. 25), и т. д.

Таким образом, помимо памяти, отведённой для элементов сортируемого массива, необходима память для размещения бинарного дерева изузлов, а также память дляэлементов отсортированного массива. Число сравнений при реализации метода равно.

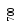
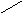
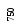
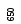
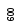
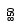
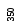
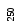
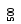
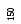
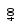
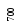
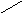
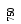
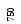
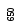
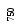
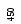
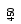
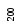
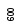
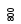
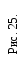
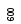
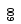
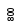
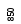
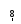
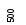
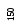
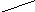
4.5.4. Пирамидальная сортировка

Полное бинарное дерево обычно хранится в последовательных ячейках памяти; при этом узлы уровня в порядке слева направо располагаются за узлами уровня(рис. 26). Родитель узла с номеромимеет номер(целая часть числа), а его непосредственные потомки ― номераи.

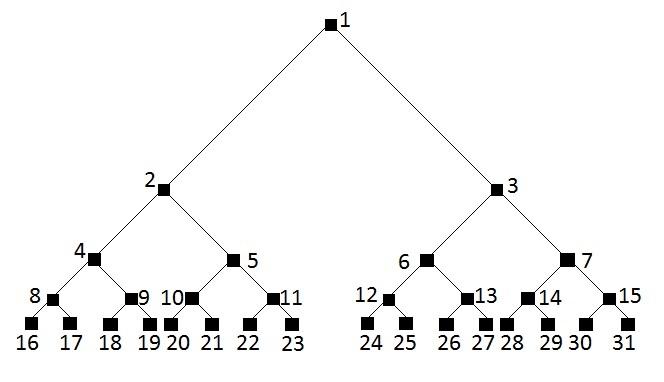Рис. 26.

Определение. Массив ключей , представленный бинарным деревом, называетсяпирамидой, если

, , (*)

то есть ключ в каждом узле не меньше обоих своих непосредственных потомков.

Заметим, что соотносится си так же, как связаны родством в полном бинарном дереве соответствующие узлы (и — левый и правый потомки узла ). Поскольку число элементов массива может не совпадать с числом узлов полного бинарного дерева, то пирамиду удобно представлять как бинарное дерево со следующими свойствами:

1) все листы имеют уровень или;

2) если удалить листы уровня получится полное бинарное дерево;

3) листы уровня заполняют левый сплошной отрезок (рис. 27).

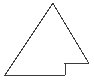
Рис. 27.

Поскольку неравенства (*) распространяются дальше по потомкам, то в пирамиде ключ в каждом узле не меньше всех своих потомков (хотя, возможно, меньше соседних ключей того же уровня и их потомков).

В частности, для пирамиды имеем:

и ;

и ;и;

и ;и, и т. д.

Из определения пирамиды следует, что на её вершине находится максимальный ключ: .

Пирамидальная сортировка массива проводится в три этапа:

1. Массив преобразуется в пирамиду путём перестановки некоторых элементов.

2. Вершина пирамиды перемещается в правый край массива, меняясь местами с находившимся там элементом.

3. Осуществляется описываемая ниже процедура «протаскивания» (или «просеивания») нового значения через дерево.

В результате протаскивания в вершине пирамиды (то есть новым ключом ) опять оказывается элемент, максимальный из ещё не отсортированных. Он удаляется из пирамиды, занимая очередное (справа налево) место в конце массива путём обмена местами на-й итерации с. При этом не отсортированными (и, значит, ещё подлежащими протаскиванию) остаются элементы. Этапы 2) и 3) циклически повторяются до исчерпания неотсортированной части массива.

Построение пирамиды. 1) Первый элемент исходного массиваставится в корень дерева; элементыи― его дети. Для того чтобы подмассивстал пирамидой, сравниваемс. Если оказывается, томеняется местами с соответствующим из двух детей. Теперь― пирамида.

2) Теперь рассматривается как вершина дерева с детьми, и оно также превращается в пирамиду сравнениемси, возможно, обменом местамис соответствующим из двух детей. Далееобменивается местами с, если. Теперь пирамиду образуют.

3) Далее в пирамиду превращается дерево с вершиной и детьми, после чего, возможно, обменивается местами с. Теперь пирамиду образуют.

.

.

.

) Наконец, в пирамиду превращается дерево с корнем и детьми, после чего, как и для других узлов, «идут наверх» сравнения и обмены местами с родителем вплоть до.

Теперь весь массив образует пирамиду. На её вершине находится максимальный элемент. Правая граница неотсортированной части массива. В процессе пирамидальной перестройки массив оставался в исходной области памяти

Перемещение вершины. После того, как пирамида построена, вершина (максимальный из ещё неотсортированных элементов) удаляется из неё, меняясь местами с крайним справа элементом ещё неотсортированной части массива(в первый раз — с). Номер правой границы неотсортированной части уменьшается на единицу (в первый раз —становится равным).

Протаскивание элементов через пирамиду. После перемещения вершины в отсортированную часть дерево перестаёт быть пирамидой, поскольку ключ в её вершине перестаёт быть максимальным (таковым теперь является бóльший из двух элементов первого уровня). Для восстановления пирамиды вершина протаскивается через дерево. Это означает, что, двигаясь по дереву вниз,меняется местами с бóльшим из двух своих детей до тех пор, пока оба они не окажутся меньше. В результате в вершине снова оказывается максимальный элемент неотсортированной части массива.

Зацикливание этапов перемещения вершины и протаскивания вплоть до исчерпания пирамиды даёт алгоритм пирамидальной сортировки:

╔

Ш.1. Начальная установка: ;.

Ш.2. Преобразование массива в пирамиду при :

если , то

;

;

;

иначе (, ключивыстроены в пирамиду)

;

;

;

если , то

;

завершить алгоритм.

Ш.3. Начало протаскивания (в данный момент при

; припомещена на

нужное место):

.

Ш.4. Продвижение вниз:

;

;

если , то

перейти к Ш.5;

если , то

перейти к Ш.6;

если , то

перейти к Ш.8.

Ш.5. Отыскание большего потомка:

Если , то

.

Ш.6. Если перейти кШ.8.

Ш.7. Подъём большего потомка наверх:

;

перейти к Ш.4.

Ш.8. Занесение элемента на нужное место в пирамиде

(завершение её протаскивания):

;

перейти к Ш.2.

╚

В процессе сортировки элементы меняются местами в пределах исходной области памяти.

Эффективность сортировки по времени определяется величиной . Эту процедуру не следует применять при небольших значениях размера массива , но она эффективна при больших и становится сравнима с сортировкой Шелла.Недостатком метода следует считать то обстоятельство, что время работы алгоритма не зависит от числа инверсий в исходном массиве: изначально «более или менее упорядоченные», сортируются так же долго, как и «хаотические».