4.3.2. Метод бинарных вставок

Результат проверки неравенства даёт наибольшую информацию, когда он позволяет отбросить максимально возможное число равновероятных вариантов (см. [17]). В силу симметрии число отбрасываемых вариантов следует по возможности уменьшать вдвое.

При сортировке бинарными вставками ключ сравнивается с ключом, номер которогозанимает среднее положение в ряду уже упорядоченных ключей. Еслинечётно, то; есличётно, то можно выбрать в качествелюбой из двух номеров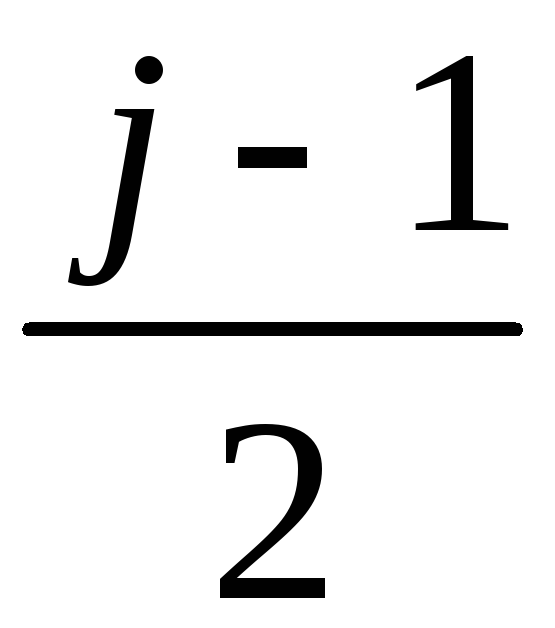или 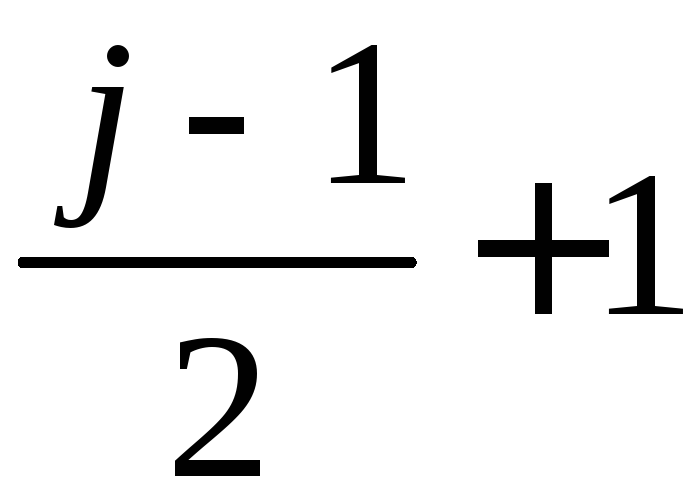. После этого средний номер выбирается уже в (два раза более коротком) ряду, если, либо в ряду, если, и т. д.

Этот метод экономит затраты времени на сравнение ключей, но не меняет количество перестановок элементов, которое по-прежнему есть .

4.3.3. Метод двухпутевых вставок

Этот метод ориентирован на минимизацию числа необходимых в среднем переписываний данных во время их сортировки.

Для размещения отсортированного массива отводится область свободной памяти, и элементпомещается в её середину. Место для последующих элементов высвобождается путём сдвигов влево или вправо, в зависимости от того, в какую сторону число необходимых сдвигов меньше. По сравнению с методом простых вставок машинное время экономится примерно наполовину, хотя усложняется программа.

Пример. Для совокупности данных

метод двухпутевых вставок приводит последовательно к следующим спискам:

Метод Шелла (сортировка с убывающим смещением). В этом методе экономия в среднем машинного времени достигается за счёт того, что переставляются не соседние, а значительно более удалённые друг от друга элементы. В то время как перестановка соседних элементов, нарушающих упорядоченность, уменьшает общее количество инверсий в массиве лишь на единицу, перестановка удалённых друг от друга элементов в методе Шелла может уменьшить его на большее число.

На промежуточных стадиях сортируются либо сравнительно более короткие массивы, либо уже сравнительно хорошо упорядоченные массивы с малым числом инверсий.

Если, например, исходный список содержит элементов, то сначала — первый проход ― упорядочиваются восемь двучленных списков со смещением на:

.

Затем на втором проходе упорядочиваются четыре четырёхчленных списка со смещением на :

На третьем проходе упорядочиваются два восьмичленных списка со смещением на :

и

.

Наконец, на последнем шаге сортируется весь список со смещением .

В общем случае набор из убывающих смещенийдля разбивки списка на части может выбираться разными способами и выступает в роли настраиваемого параметра. Сортировка внутри каждой из групп элементов, отстоящих напозиций, может осуществляться, например, методом простых вставок.

Алгоритм сортировки методом Шелла содержит следующие этапы.

╔

- внешний цикл по ― перебор смещений:

- ― работа с очередным значением смещения;

- вложенный цикл по ― для сортиро-

вки элементов, отстоящих на позиций:

- ― номер крайнего справа отэлемента из

уже упорядоченных в группе;

- номера остальных последовательно уменьшаются на

;

- ― данные вставляемого элемента;

он будет продвигаться влево, пока не дойдёт до

элемента с меньшим значением ключа;

- вложенный цикл по с шагомпока;

- если то:

- :ставится на место;

- принудительный выход из цикла по ;

- ― сдвиг вправо элементов с бóльшим

значением ключа с целью высвобождения

места вставляемому элементу.

╚