Глава 4. Сортировка в оперативной памяти

4.1. Исходные понятия

Будем рассматривать задачу упорядочения совокупности данных , имеющих единообразную структуру вида [поле значений]+[ключ], в предположении, что на множестве значений ключей имеется отношение порядка “<”, удовлетворяющее двум условиям:

- закон трихотомии: для любых значений ивыполняется ровно одно из соотношений;

- закон транзитивности: (и).

Будем писать , если или.

Сортировкой называется упорядочение данных в порядке возрастания или убывания значений ключевого поля (для краткости будем говорить о возрастании или убывании самого ключа). Таким образом, при решении задачи сортировки ищется такая перестановка исходного множества номеров, при которой

.

Сортировка называется устойчивой, если она сохраняет относительный порядок для одинаковых значений ключа:

.

Устойчиво сортирующая перестановка единственна. Требование устойчивости существенно, если данные уже упорядочены по одному или нескольким другим (вторичным) ключам, не влияющим на основной ключ, и нежелательно разрушать эту упорядоченность.

Алгоритмы сортировки находят большое практическое применение. Они всегда сопровождают процессы обработки и хранения больших объемов информации. Выбор конкретного метода сортировки зависит как от структуры обрабатываемых данных (массивы, списки, деревья и т. д.), так и от архитектуры используемого компьютера.

Алгоритмы сортировки делят на два класса:

- внутренняя сортировка, при которой все данные хранятся и перемещаются в оперативной (быстрой) памяти с произвольным доступом ― в этом случае упорядочиваемые данные будем называть массивом;

- внешняя сортировка, когда из-за слишком большого объёма данные размещаются на внешних носителях ― в этом случае упорядочиваемые данные будем называть файлом.

В случае внутренней сортировки важно по возможности минимизировать количество наиболее часто повторяемых действий ― сравнений и обменов. Для внешней сортировки важно минимизировать число обращений к устройствам с медленным доступом (магнитным лентам, барабанам, дискам).

Рационально построенные алгоритмы сортировки элементов предполагают в среднемпроходов по всей совокупности данных и затрачивают время. Отметим, что выбор основания логарифма не играет существенной роли, поскольку логарифмы с разными основаниями пропорциональны, а оценка с использованием символапроизводятся с точностью до постоянного множителя:

,

где .

Разные алгоритмы сортировки различным образом воздействуют на расположение сортируемых данных в памяти. Некоторые из них фактически переставляют элементы в памяти, то есть меняют их физические адреса. Другие сохраняют исходные физические адреса, но составляют дополнительную таблицу, содержащую сортирующую перестановку. В случае громоздкой структуры данных возможно также составление дополнительной таблицы, содержащей адресные ссылки на элементы и соответствующие значения ключа сортировки; после этого сортировка происходит только внутри этой таблицы. Последнее особенно предпочтительно, когда данные располагают несколькими ключами, и может потребоваться сортировка по различным комбинациям ключей.

Ключи сортировки часто не содержатся в исходной структуре данных в качестве отдельных полей, а имеют вид функций от поля (или полей) значений. Например, можно задать сортировку по количеству букв в поле “фамилия”, по лексикографической (алфавитной) упорядоченности “имён” и/или “отчеств” и т. п.

При сортировке списка возможно введение в каждый элемент вспомогательного поля связи, содержащего адрес следующего в указанном порядке элемента.

Методы сортировки разбиваются на несколько классов в зависимости от принципов, положенных в основу сортирующего алгоритма (рис. 22).

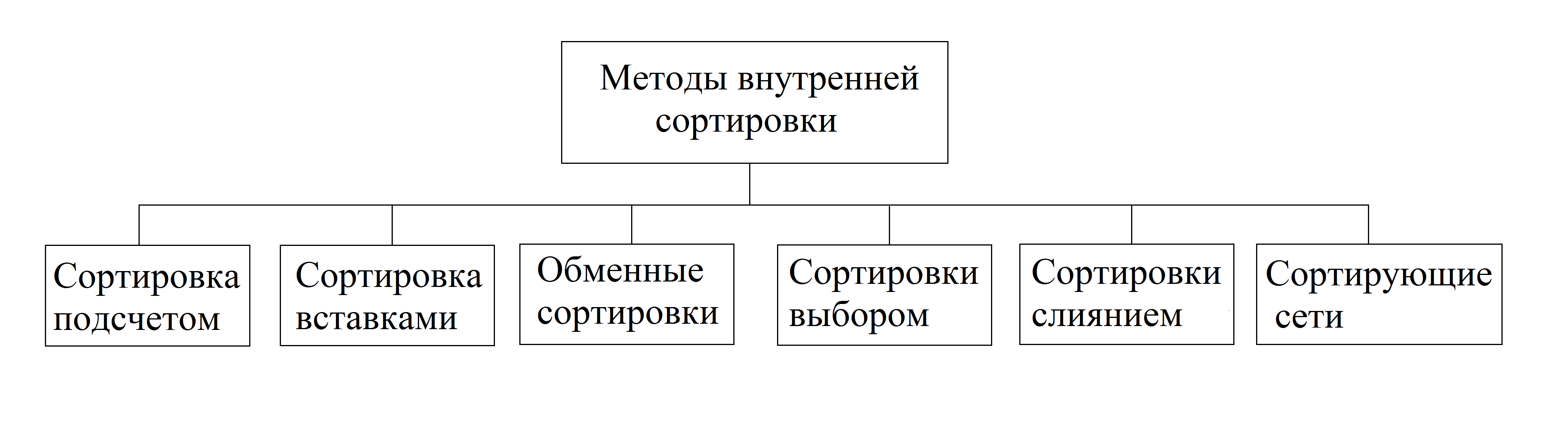
Рис. 22.

Внутри каждого класса содержатся методы, основанные на различных идеях (рис. 23).