2.5. Цепь переменного тока с ёмкостью

Проанализируем процессы в цепи переменного тока, представленной на рис.2.18.

Рис.2.18. Цепь переменного тока с ёмкостью

Ёмкость при прохождении синусоидального электрического тока характеризует свойство накапливать заряды и образовывать электрическое поле. При этом напряжение на зажимах конденсатора определяется по формуле

(2.16)

Cравнивая выражения для мгновенных значений тока и напряжения в цепи с ёмкостью, имеем: i = 0; u =-, откуда угол сдвига фаз =u - i =-.

Таким образом, ток в цепи с ёмкостью опережает по фазе напряжение на угол - (рис. 2.19).

Рис.2.19. Зависимости мгновенных значений напряжения, тока и мощности цепи переменного тока с ёмкостью

Из формулы (2.16) выведем закон Ома для амплитудных значений: или

. (2.17)

Введем обозначение: , где - емкостное сопротивление. Действительно, если , то 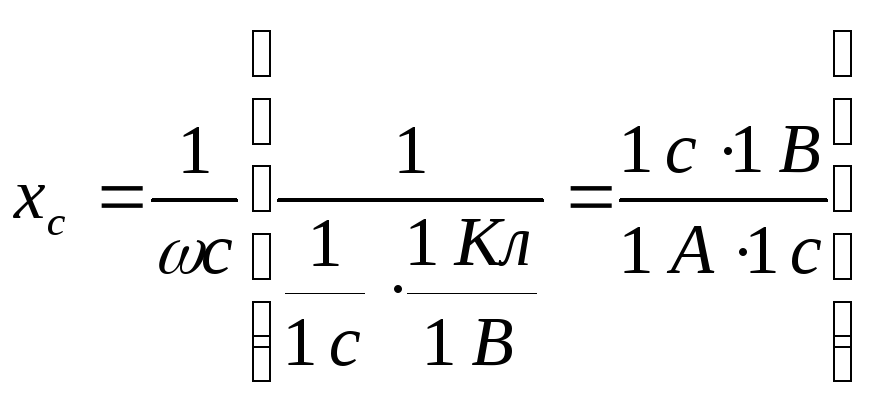измеряется в Омах.

Закон Ома для действующих значений напряжения и тока имеет выражение:

. (2.18)

Для комплексных чисел закон Ома записывается в виде

. (2.19)

Диаграммы в векторном и комплексном видах представлены на рис. 2.20.

Рис.2.20. Векторные диаграммы действующих значений тока и напряжения цепи переменного тока с ёмкостью в векторном и комплексном виде

Так как напряжение на ёмкости отстает от тока на угол -, который изменяется по косинусоиде, то мгновенную мощность выразим в виде:

, (2.20)

где

Мгновенная мощность p имеет частоту 2ω, но в отличие от индуктивности, здесь мощность положительна, пока возрастает напряжение на ёмкости. Происходит накопление энергии электрического поля на конденсаторе. Затем конденсатор разряжается на источник, и мощность становится отрицательной.

Из рис. 2.19 видно, что средняя или активная мощность P = Pср= 0. Амплитуда колебаний мощности в цепи с ёмкостью называют реактивной емкостной мощностью:

. (2.21)

Единицей реактивной ёмкостной мощности является вольт-ампер реактивный (вар).

2.6. Неразветвлённая цепь переменного тока с активным сопротивлением, индуктивностью и ёмкостью. Резонанс напряжений

Рассмотрим неразветвлённую электрическую цепь (рис. 2.21).

Пусть , тогда .

Построим векторную диаграмму при условии, что действующие значения напряжений

Из векторной диаграммы (рис.2.22) следует:, откуда . Но , следовательно .

Рис.2.21. Схема неразветвлённой электрической цепи с активным сопротивлением индуктивностью и ёмкостью

Рис.2.22. Векторная диаграмма действующих значений тока и напряжений () цепи переменного тока с активным сопротивлением индуктивностью и ёмкостью

Введя обозначение полного сопротивления цепи , найдем:

. (2.22)

Разность между индуктивным и емкостным сопротивлениями называют реактивным сопротивлением цепи X = XL - XC. Учитывая это, получим треугольник сопротивлений для цепи с R, L и C (рис. 2.23).

При XL > XC реактивное сопротивление положительно и угол > 0.

Аналогично можно построить векторную диаграмму для действующих значений напряжений (рис. 2.24) и треугольник сопротивлений (рис. 2.25).

Рис.2.23. Треугольник сопротивлений цепи переменного тока с активным сопротивлением, индуктивностью и ёмкостью ()

Рис.2.24. Векторная диаграмма действующих значений тока и напряжений () цепи переменного тока с активным сопротивлением индуктивностью и ёмкостью

Рис.2.25. Треугольник сопротивлений цепи переменного тока с активным сопротивлением, индуктивностью и ёмкостью ()

При XL < XC реактивное сопротивление X отрицательно и угол < 0. Если UL = UC и XL = XC , то векторную диаграмму можно представить в виде рис. 2.26, а зависимость тока от частоты в виде рис.2.27.

В этом случае наступает резонанс напряжений, когда ток в цепи совпадает по фазе с напряжением источника. При этом угол = 0, так как реактивное сопротивление равно нулю.

Рис.2.26. Векторная диаграмма резонанса напряжений

Рис.2.27. Зависимость тока от частоты питающей сети для резонанса напряжений

При резонансе напряжений частота источника равна собственной частоте колебаний LC-контура. Если , где f - частота источника питания, то можно записать . Решив это уравнение относительно f, получим

. (2.23)

На основании рис.2.26, 2.27 следует, что признаками резонанса напряжений являются:

а) полное сопротивление цепи равно активному сопротивлению Z = R;

б) ток в цепи совпадает по фазе с напряжением источника и имеет максимальное значение;

в) напряжение на индуктивной катушке равно напряжению на конденсаторе и каждое в отдельности превышает напряжение источника;

г) коэффициент мощности cos = 1.

На рис.2.28 изображены примерные функциональные зависимости индуктивных и емкостных напряжений, тока и коэффициента мощности в зависимости от изменения ёмкости конденсатора, где Cp - резонансная ёмкость.

Рис.2.28. Примерное изображение зависимостей UL, UC, , cos от изменения ёмкости конденсатора C

Количественная оценка соотношения энергий источника, катушки индуктивности и конденсатора при резонансе напряжений характеризуется добротностью контура:

. (2.24)

Величину при резонансе называют волновым сопротивлением контура.