2.2. Представление синусоидальных величин аналитически, графически, вращающимися векторами, комплексными числами

Аналитически синусоидальные величины можно записать при помощи уравнений с тригонометрическими функциями:

(2.6)

Электрические углы , -, , называются начальными фазами. Аргументы , , , называются начальными фазами синусоид. Временной сдвиг начальных фаз напряжения и тока называется углом сдвига фаз

. (2.7)

Синусоидальные величины, записанные аналитически, можно изобразить графически (рисунки 2.4, 2.5, 2.6) в виде мгновенных значений ЭДС, напряжения и тока.

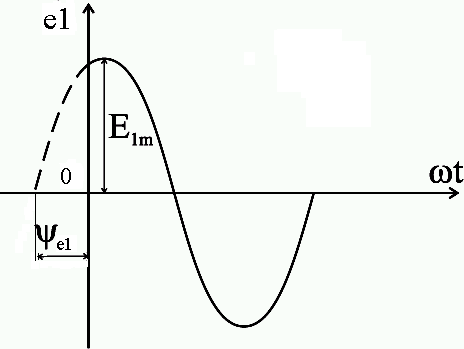
Рис.2.4. Мгновенная ЭДС с положительной начальной фазой

Рис.2.5. Мгновенная ЭДС с отрицательной начальной фазой

Рис.2.6. Мгновенные значения напряжения и тока, имеющие угол сдвига фаз

При расчете цепей переменного тока часто приходится производить операции сложения и вычитания ЭДС, токов и напряжений. Графически и аналитически выполнять такие операции достаточно громоздко. Для этих целей используется построение векторных диаграмм на декартовой или комплексной плоскостях.

На рис. 2.7 и 2.8 приведено изображение выше рассмотренных синусоидальных величин на декартовой плоскости в виде вращающихся векторов.

Совокупность векторов, изображающих синусоидальные ЭДС, напряжения и токи одной частоты, называются векторными диаграммами.

Рис.2.7. Векторное изображение синусоидальных ЭДС

Рис.2.8. Векторное изображение синусоидальных значений напряжения и тока, имеющих угол сдвига фаз

На рис. 2.9 и 2.10 показано сложение и вычитание векторов на векторных диаграммах. Здесь сложение двух синусоид и , представленных синусоидой , выполнено в виде сложения вращающихся векторов на декартовой плоскости . Аналогично выполняется вычитание векторов ЭДС .

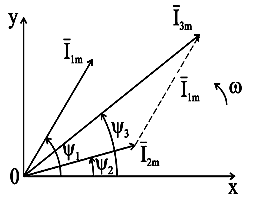
Рис.2.9. Сложение векторов токов на декартовой плоскости

Рис.2.10. Вычитание векторов ЭДС на декартовой плоскости

Изображение синусоидальных величин на комплексной плоскости осуществляется комплексными числами.

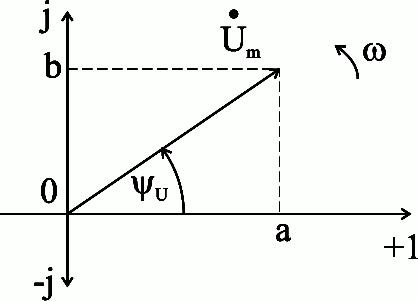
Рис.2.11. Изображение вектора напряжения синусоидальной величины на комплексной плоскости

На комплексной плоскости (рис. 2.11) по оси абсцисс откладываются вещественные (действительные) величины, по оси ординат - мнимые величины ().

Пусть мгновенное напряжение , тогда комплексная амплитуда напряжения графически изображается вектором , вращающимся против часовой стрелки с угловой частотой ω. Вектор с модулем и аргументом символически изображается в показательной форме . Удобно модулем комплексного выражения брать не амплитудное, а действующее значение. Тогда можно написать тригонометрическую форму изображения действующего значения комплексного напряжения , называемого формулой Эйлера. Действующее значение комплексного напряжения можно выразить в алгебраической форме . Аргумент комплексного числа . Если , то комплексное сопротивление цепи можно изобразить в виде:

,

где r - активное сопротивление, x - реактивное сопротивление, z - полное сопротивление.