3.3. Обрыв фазы и короткое замыкание фазы без нулевого провода при соединении источников энергии и потребителей звездой
3.3.1. Обрыв фазы a
Рассмотрим
электрическую схему рис.3.12, в которой
,
,
,
.
По первому закону Кирхгофа:
;
.
(3.7)
Преобразуем
рис.3.12 в рис.3.13, откуда следует, что если
,
тогда
=
=
.
(3.8)
Рис.3.12. Электрическая схема трёхфазной системы, соединённой звездой, без нулевого провода с выключенной фазой
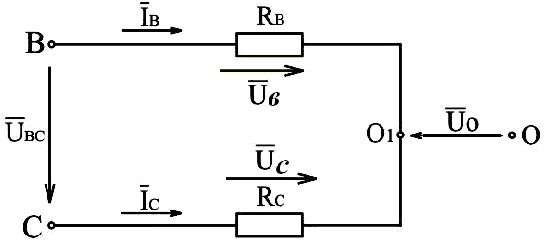
Рис.3.13. Схема, поясняющая построение векторной диаграммы
По второму закону Кирхгофа:
;
;
.
(3.9)
Используя формулы (3.7), (3.8), (3.9) построим векторную диаграмму (рис.3.14).
Рассмотрим пример.
Пусть
фазные генераторные напряжения
равны 220B,
тогда из векторной диаграммы следует,
что
=
= 110B
и
=
=
=
=
220
∙
= 190B,
Рис.3.14. Векторная диаграмма напряжений и токов трёхфазной системы, соединённой звездой, без нулевого провода с выключенной фазой
3.3.2. Короткое замыкание фазы a
Рассмотрим
электрическую схему рис.3.15, в которой
,
,
=
,
= 0.
Воспользуемся преобразованиями:
,
так
как
,
,
(3.10)
где
-
вектор отрицательного линейного
напряжения;
,
(3.11)
где
-
вектор линейного напряжения.
По первому закону Кирхгофа:
;
.
(3.12)
Используя формулы (3.10), (3.11), (3.12) построим векторную диаграмму, приведённую на рис.3.16.
Рис.3.15. Электрическая схема трёхфазной системы, соединённой звездой, без нулевого провода с коротким замыканием фазы
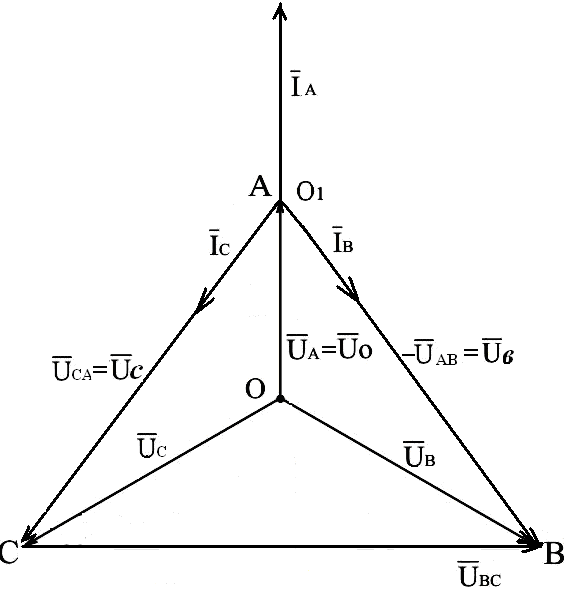
Рис.3.16. Векторная диаграмма напряжений и токов трёхфазной системы, соединённой звездой, без нулевого провода с коротким замыканием фазы
Рассмотрим пример.
Пусть
Ом,
,
10А,
10А.
Из векторной диаграммы следует:
∙
10
∙
;
= 10
∙
=17,3A.
3.4. Соединение источников и приёмников электроэнергии треугольником. Соотношения между фазными и линейными напряжениями и токами при симметричной и несимметричной нагрузках
Рассмотрим
схему рис.3.17, в которой трёхфазный
генератор
,
,
и три активных приемника
,
,
соединены треугольником.
Рис.3.17. Электрическая схема трёхфазной системы, представленной в виде трёхфазного генератора и активной трёхфазной нагрузки, соединённых треугольником
Из
схемы видно, что линейные напряжения
,
,
являются одновременно фазными напряжениями
,
(3.13)
токи
,
,
являются линейными и токи
,
,
являются фазными.
По первому закону Кирхгофа:
.
(3.14)
При
симметричной нагрузке
.
Из выражений (3.14) следует, что геометрическая
сумма линейных токов
.
На рис.3.18 приведена векторная диаграмма напряжений и токов для симметричной нагрузки, соединённой треугольником.
Из
диаграммы видно:
,
где
;
.
Рис.3.18. Векторная диаграмма напряжений и токов для симметричной нагрузки, соединённой треугольником
Таким образом, при соединении треугольником соотношение между линейными и фазными токами выражается формулой:
.
(3.15)
Если
нагрузка несимметрична, то
.
Тогда, используя выражения (3.14), можно
построить векторную диаграмму напряжений
и токов следующего вида:
Рис.3.19. Векторная диаграмма напряжений и токов для несимметричной нагрузки, соединённой треугольником