Вопрос №17

8

Вопрос №17.

Небесная сфера. Системы сферических координат, используемые в мореходной астрономии. Связь с географическими координатами. Параллактический треугольник и его решение по формулам и таблицам.

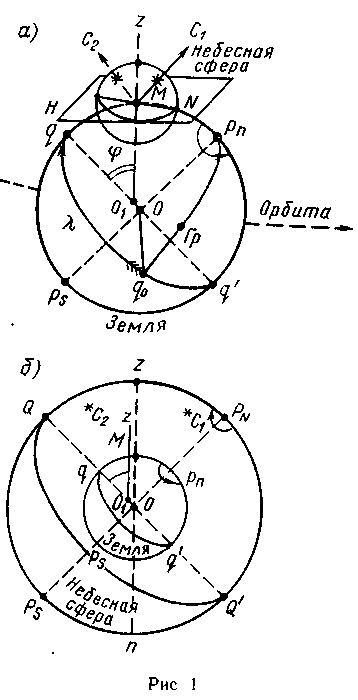
Небесная сфера.

Наблюдатель М, находящийся на поверхности Земли, участвует в ее су­точном вращении и орбитальном обраще­нии, вследствие чего направления на светила С1, С2 (рис 1, а) изменяются. Для упрощения решения астрономиче­ских задач и наглядности движений вво­дится вспомогательная сфера, получив­шая название небесной сферы. Можно представить сферу построенной около места наблюдателя М (см. рис. 1, а) или описанной около центра О Земли (рис. 1, б).

Небесной сферой называется вспомо­гательная сфера произвольного радиуса, к центру которой параллельно перене­сены основные линии и плоскости на­блюдателя и Земли и направления на светила.

Основным направлением наблюдате­ля М является его вертикаль, или отвесная линия, z01 (см. рис. 1), положе­ние которой в данной точке Земли по­стоянно и определяется направлением силы притяжения. Пересечение верти­кали с поверхностью Земли представля­ет место М наблюдателя. Положение точки М на Земле определяется ее географической широтой φ (угол меж­ду отвесной линией и плоскостью эк­ватора) и долготой λ (двугранный угол между меридианами — гринвичским Гр и наблюдателя М, равный дуге q0q). Введение небесной сферы позволяет по­строить аналогичные системы координат для светил.

П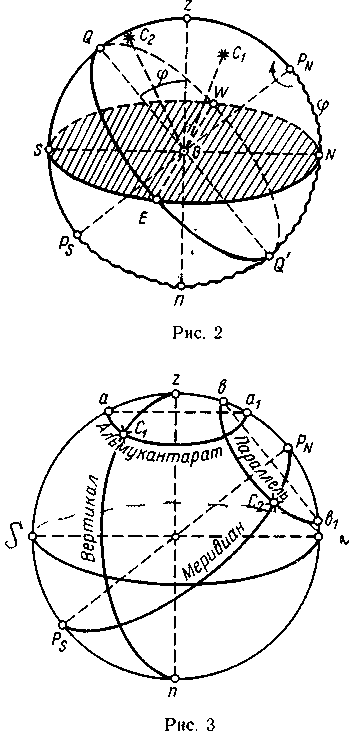ри построении небесной сферы ее центр помещают в произвольной точке О (рис. 2) и через нее проводят линии, параллельные линиям наблюдателя М (см. рис. 1, б). Линия, параллельная вер­тикали z01 называется отвесной линией zn, а точки пересечения ее со сферой —зенитом z и надиром n. Линия, парал­лельная оси pnps, Земли (см. рис. 1, а), представляет на сфере ось мира PNPs, вокруг которой вращается сфера. Точ­ки пересечения ее со сферой называются полюсами мира: северным PN и юж­ным Ps (они соответствуют полюсам Земли).

Плоскость Н истинного горизонта наблюдателя М (см. рис. 1, а), проведен­ная через центр сферы, дает в сечении со сферой истинный горизонт — большой круг NESW, перпендикулярный отвес­ной линии zn.

Плоскость экватора Земли, перене­сенная к центру О сферы, дает в сечении со сферой небесный экватор — большой круг QWQ'E, плоскость которого пер­пендикулярна оси мира.

Плоскость pNMqps (см. рис. 1, а) — географического меридиана наблюдате­ля М. проведенная через центр сферы, дает в сечении с ней меридиан наблюда­теля— большой круг PNzQPsQ'. Ось мира PNPS разделяет меридиан наблю­дателя на полуденную часть PNzPs, включающую зенит, и полуночную PNnPs (на рис. 2 волнистая линия). Эти части меридиана Солнце пересека­ет в полдень и в полночь, отсюда их на­звания.

Основные круги сферы делят ее на части: горизонт — на надгоризонтную и подгоризонтную (где светила не вид­ны); небесный экватор — на север­ную (PN) и южную (Ps); меридиан наблюдателя NzS — на восточную (E) и западную (W).

Истинный горизонт наблюдателя де­лится на направления. Пересечение пло­скостей меридиана и горизонта дает полуденную линию N—S, а плоскостей экватора и горизонта - линию Е —W. На сфере пересечение этих линий дает точки N, Е, S, W, которыми горизонт разделяется на четыре четверти: NE, SE, SW, NW и далее делится на румбы и градусы. Можно представить его в виде картушки компаса.

Полюс мира, расположенный над го­ризонтом, называется повышенным по­люсом. Его наименование совпадает с широтой наблюдателя: в северной ши­роте — PN, в южной — Ps. Возвышение полюса над горизонтом, т. е. дуга NPN, равно широте, так же как дуга zQ (см. рис. 2).

Если из центра сферы провести на­правления на светила, то на ее поверх­ности получаются точки С1, С2, назы­ваемые видимыми местами светил (в дальнейшем просто светила). На сферу можно также спроектировать и другие плоскости и объекты: плоскость орбиты Земли даст эклиптику, орбиты Луны — видимую орбиту Луны, орбиты спутни­ка — видимую орбиту спутника и т. п

Изображения сферы.

Изображения одной и той же небесной сферы могут быть разными: для местного наблюдате­ля на плоскости его меридиана с центром в глазу наблюдателя (см. рис. 1 и 2) или для любого наблюдателя на Земле с центром в центре Земли (см. рис. 9) или в центре солнечной системы (см. рис. 23). Надо твердо усвоить, что все это — изображения одной вспомога­тельной сферы в различных видах и что из одного вида легко получить другой (сравнить рис. 1, б и 9). Для задач каж­дого типа удобно определенное изобра­жение сферы, без лишних деталей.

Введение небесной сферы приводит к упрощениям:

замене направлений — точками,

плоскостей и углов — круга­ми;

направление в пространстве опреде­лится двумя дугами — сферическими ко­ординатами.

Движения светил можно рассматривать теперь как движение их мест вместе со сферой — от суточного вращения Земли и по сфере — от соб­ственных движений и других причин.

Системы вспомогательных кругов.

Для удобства построения сферических координат на сфере вводят системы вза­имно перпендикулярных кругов. Круги, связанные с отвесной линией:

верти­калы — большие круги, плоскости ко­торых проходят через отвесную линию (перпендикулярные горизонту), напри­мер zС1n на рис 3,

альмукантараты — малые круги аа1, плоскости которых па­раллельны горизонту

Вертикал, прохо­дящий через точки Е. W, называется первым вертикалом

Круги, связанные с осью мира:

не­бесные меридианы (или круги склонений) — большие круги, плоскости ко­торых проходят через ось мира (перпен­дикулярные экватору), например PNC2Ps на рис. 3;

параллели — малые круги bb1 плоскости которых параллельны экватору. Эти круги аналогичны гео­графическим меридианам и параллелям на Земле. Небесный меридиан PNzPs лежит в плоскости географического ме­ридиана наблюдателя М (см рис 1, б) и поэтому называется меридианом на­блюдателя (иногда местным меридианом); одновременно он является и вертикалом наблюдателя

Системы сферических координат, используемые в мореходной астрономии.

С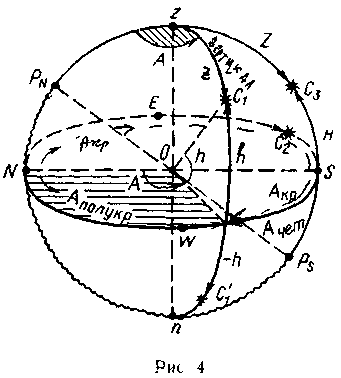истемы координат на небесной сфе­ре строятся относительно двух взаимно перпендикулярных кругов сферы, по­добно широтам и долготам на земном глобусе В этом случае получаются сфе­рические прямоугольные координаты Применяются и сферические полярные координаты — по сферическому углу при какой-либо точке и расстоянию от нее На сфере эти системы часто совпадают. Из известных в сферической астроно­мии пяти систем небесных координат в мореходной астрономии применяются: горизонтная, две экваториальные и, из­редка, эклиптическая

Горизонтная система координат.

Основными кругами (осями координат) в этой системе являются

истинный го­ризонт и

меридиан наблюдателя:

основ­ным направлением

отвесная линия zn

Положение точки или светила на сфере определяется двумя координата­ми:

высотой и

азимутом (рис. 4, сфера на нем для φN повернута W-м к зрите­лю)

Высотой h светила называется дуга его вертикала от истинного горизонта до места светила

Угол при центре сфе­ры, измеряемый этой дугой, также на­зывают высотой.

Этот угол измеряется при наблюдениях. Высоты считаются в пределах от 0 до ±90°; с «+» над го­ризонтом, с «—» под горизонтом, напри­мер светило С1 имеет h = 46°, светило С1’ имеет h —30 , высота зенита +90°, надира —90 и т п

Азимутом А светила называется дуга истинного горизонта между мери­дианом наблюдателя и вертикалом све­тила Эта дуга измеряет плоский угол при центре сферы или сферический угол А при зените, которые поэтому, также называют—азимутами.

В мореходной астрономии применяют три системы счета азимутов: полукруго­вой, круговой и четвертной.

Полукруговой азимут считается в пределах О—180° от полуночной части ме­ридиана наблюдателя в сторону Е или W до вертикала светила, например А = N100°W (см рис 4) В северной ши­роте начальной точкой счета является N, в южной — S, поэтому первая бук­ва наименования азимута совпадает с широтой, вторая — с половиной сферы, где расположено светило. Этот счет ази­мутов применяют при решении сфериче­ских треугольников по формулам и по таблицам ВАС—58.

Круговой азимут считается от точки N в сторону Е до вертикала светила в пределах 0—360°, т. е. совпадает с ис­тинным пеленгом светила, например для светила C1 А = ИП = 260°. Этот счет применяют при определении ∆K и при прокладке.

Четвертый азимут считается по чет­вертям — от ближайшей части меридиа­на наблюдателя до вертикала светила в пределах 0—90°, например, светило С1 имеет А = 80°SW. Этот счет применяют в формуле синусов и ТВА—57.

Необходимо уметь свободно перехо­дить от одной системы счета азимута к другим — это постоянно требуется на практике. Например, для светила С2 (см. рис. 4) имеем: полукруговой А = N150°E; круговой А = 150°; четверт­ной А = 30°SE. Положение светила С1 в горизонтной системе запишется так: А = 260°; h = 46°. Одна горизонтная координата определяет на сфере положение одного круга: азимут — по­ложение вертикала, высота — альмукан­тарата.

Полярные координаты. Положение точки на сфере может быть определено и без построения горизонта — непо­средственно при зените. Зенит является полюсом, а меридиан наблюдателя — полярной осью координат A и z. Азимут в полярных координатах определяется как угол при зените в полукруговом сче­те (см. рис. 4).

Зенитным расстоянием z называется дуга вертикала от зенита до места свети­ла в пределах О—180° так, на рис.4 z = 44°. Зенитное расстояние связано с высотой соотношением

Дуга z измеряет центральный угол z между отвесной линией и направле­нием на светило (этот угол измеряется береговыми инструментами). Полярные координаты применяются при решении сферических треугольников.

Меридиональная высота H - высота све­тила, расположенного на меридиане на­блюдателя. Ей придается наименование той точки горизонта, над которой она измерена, например, для С3 H — 35°S. Наименование меридионального зенит­ного расстояния Z обратно Н. Так, для светила С3 Z = 55°N.

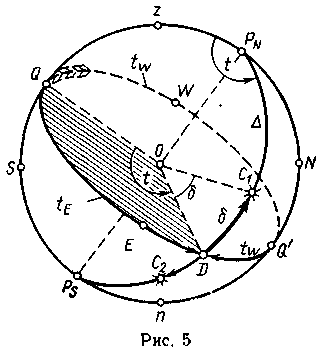
Первая экваториальная система ко­ординат.

Основным направлением в этой системе является:

ось мира PNPs,

основными кругами:

экватор и

меридиан наблюдателя.

Положение точки на сфере определяется двумя координата­ми: склонением и

часовым углом (рис. 5).

Склонением δ светила называется ду­га меридиана светила от небесного эква­тора до места светила. Угол δ при цент­ре сферы, равный этой дуге, также на­зывают склонением (его измеряют в об­серваториях). Склонения считаются от О до 90° к N или S; например, на рис. 5 для светил С1 и С2 имеем δ1 = 33°N, δ2 =26S.

Примечание. В мореходной астро­номии принято склонению придавать знак «+», если оно одноименно с широтой, и знак «—», если разноименно. В обсерваторией и геодезической астрономии, а также в ЭВМ чнак «+» придается северному склонению (и широте), знак «—» — южному

Часовым углом t называется дуга эк­ватора от полуденной части меридиана наблюдателя до меридиана светила, счи­таемая в сторону точки W от 0 до 360°. В таком счете часовой угол называют вес­товым, или обыкновенным, и наимено­вания обычно не приписывают. Кроме этого, применяется полукруговой счет часовых углов: от 0 до 180° к W или Е, который называют иногда практическим, так как он применяется при решении треугольников и в таблицах, т. е. tE = 360° — tw при tw > 180°. Для све­тила C1 (см. рис. 5) имеем t = 245°W, или t = 115°Е. Дуга экватора QD из­меряет центральный угол t или сфериче­ский угол при полюсе t, которые также называют часовыми углами.

Место светила С1 на сфере запишется теперь так: t = 245°; б = 33°N.

Одна экваториальная координата определяет на сфере положение одного круга:

ча­совой угол — положение меридиана све­тила;

склонение — параллели.

Полярные координаты. Положе­ние точки можно определить при по­люсе мира — в полярных координатах t и ∆. Часовой угол теперь определяется как угол при повышенном полюсе в полукруговом счете (на рис.5 t=115°Е).

Полярным расстоянием ∆ называется дуга меридиана светила от повышен­ного полюса до места светила, считае­мая oт 0 до 180°, например для светила С1 ∆ =57°,С2 ∆= 116°. Очевидно, что ∆ = 90° - δ.

По определению часовой угол от­считывается от плоскости географиче­ского меридиана места, поэтому на рис. 5 и аналогичных всегда изображает­ся местный часовой угол. Для других меридианов часовые углы другие.

Вторая экваториальная система ко­ординат.

В этой системе основное на­правление

ось мира,

а основными кру­гами являются

небесный экватор и

ме­ридиан точки Овна (γ).

Точка Овна, или точка весеннего равноденствия, рас­положена в пересечении экватора с эк­липтикой, т. е. связана с орбитой Зем­ли. Положение светила в этой системе определяется

с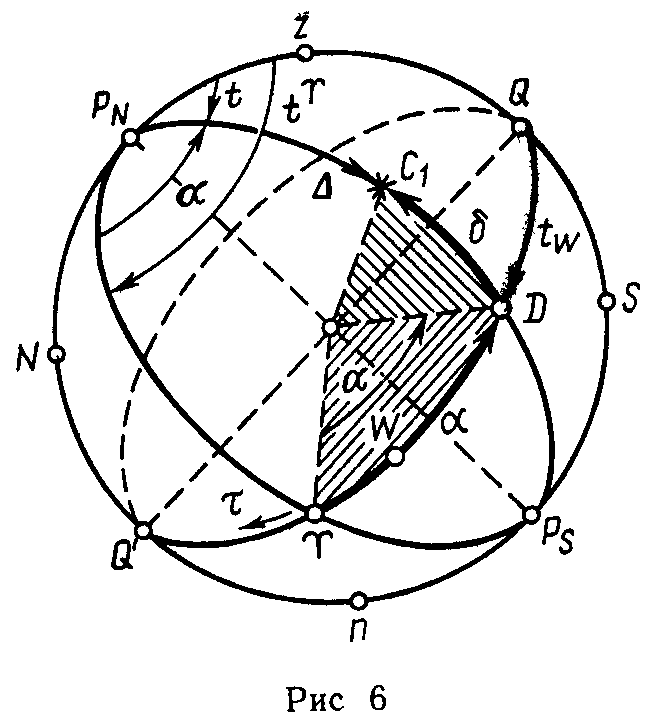клонением и

прямым вос­хождением (рис. 6).

Склонение δ в этой системе аналогично первой экваториаль­ной системе.

Прямым восхождением α светила на­зывается дуга экватора от точки Овна до меридиана светила, считаемая в сто­рону, обратную W часовым углам (т. е. в сторону Е) от 0 до 360°.

Дуге α соот­ветствуют при центре сферы и при полю­се углы а, также называемые прямым восхождением. Например, для светила С, α = 55°; б = 35°N. Вместо α в мор­ских пособиях применяется также звездное дополнение: (т=360- α)

Звездным дополнением т называют дугу экватора от точки Овна до меридиа­на светила, но считаемую в сторону W часовых углов, например для светила C1 имеем т = 305°. В отечественных по­собиях т применяется только для звезд, отсюда и его название. Направление счета прямого восхождения α совпадает с вращением Земли и ее обращением по орбите.

Полярные координаты. В этом слу­чае прямое восхождение α (или т) счи­тается как угол при полюсе между ме­ридианами точки Овна и светила, а по­лярное расстояние ∆ — аналогично пер­вой системе координат (см. рис. 6). Эта система координат аналогична геогра­фическим: α — с λ; δ — с φ.

Первая и вторая экваториальные си­стемы отличаются только положением начального меридиана: t считается от точки Q, а

α — от точки Овна (v),

по­ложение же точки Овна определяется ее часовым углом t^v, поэтому (см. рис.6)

т. е. часовой угол точки Овна (звездное время) равен сумме часового угла и прямого восхождения светила. По этой формуле (в § 23 она названа основной формулой времени) можно перейти от одной системы к другой.

Эклиптическая система координат.

В этой системе основным направлением является

ось эклиптики,

а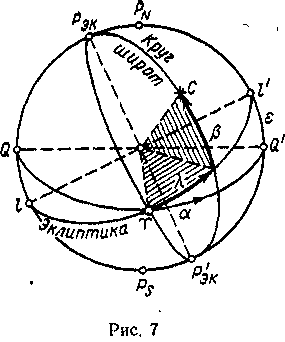 основными кругами

эклиптика (плоскость орби­ты Земли) и

круг широты точки Овна (рис. 7).

Эклиптика, как всякий большой круг, имеет ось, которая пересекает сферу в полюсах эклиптики — северном РЭК и южном Р’ЭК. Большие круги, про­ходящие через полюса эклиптики, на­зываются кругами широты (см. рис. 7).

Эклиптической широтой β называет­ся дуга круга широт от эклиптики до места светила в пределах 0—90° со зна­ком «+» к северу, «—» к югу.

Эклиптической долготой λ называется дуга эклиптики от точки Овна до кру­га широты светила — от 0 до 360° в сторону счета α. Для светила С имеем: β = +40°, λ= 60°. Эту систему приме­няют при предвычислении координат по формулам § 12, в частности на ЭВМ.

Единицы измерения сферических ко­ординат. Координаты на небесной сфе­ре являются дугами больших кругов или сферическими углами, поэтому для их измерения применяют все единицы измерения углов (градусная мера, радианная) и специальную астрономиче­скую часовую меру дуг и углов.

Часовая мера основана на историче­ски сложившемся разделении одного оборота сферы на 24 части (часа), каж­дого часа — на 60 мин и 1 мин — на 60 с. Между часовой и градусной мерой дуг (в дальнейшем—и времени) установ­лено соотношение: за 24Ч сфера повора­чивается на 360°, поэтому 360° =24Ч 15°=1Ч 1°=4м 1’=4c 0,25’=1c. В мореходной астрономии координаты измеряются до 0,1’ или до 0,5c, в прак­тической части — до 1c. Таблицы пере­хода приведены в МТ—75 (табл. 39) и МАЕ (приложение 3). Переход от гра­дусной меры к часовой осуществля­ют по схеме: делить на 15, остаток ум­ножать на 4 и т. д. (см. пример 1).

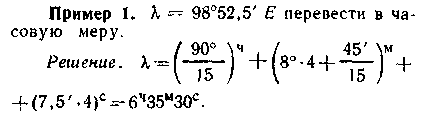
Связь с географическими координатами.

При решении конкретных задач при­меняют более удобную для данного слу­чая систему координат. Горизонтная система ориентирована в пространстве относительно отвесной линии наблюда­теля, поэтому h и А светила зависят от положения наблюдателя на Земле, и по ним можно определить его место. Часовые углы измеряют угол поворота сферы, поэтому их удобно применять при измерении времени, и т. п. В зада­чах возникает необходимость перехода от одной системы координат к другим. Самым простым является графическое построение сферы, оно необходимо так­же при изучении систем координат. При построении сферы можно использовать различные ее изображения как про­странственные, так и плоские. Для по­строения необходимо знать широту на­блюдателя φ (иногда и λ).

С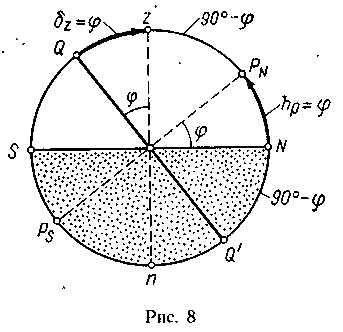вязь широты наблюдателя с коор­динатами точек сферы. В этом вопросе удобнее применить плоское изобра­жение сферы, для чего местная сфера (см. рис. 1, а и рис. 2) проектируется на плоскость меридиана наблюдателя (рис. 8).

Угол между отвесной линией zn и плоскостью небесного экватора QQ' равен географической широте по ее определению. Дуга Qz поэтому равна φ, но эта же дуга — склонение зенита, поэтому δZ = φ, т. е. склонение зенита равно широте места.

Из рис. 8 видно, что широте равны еще три дуги, остальные равны 90° - φ. Дуга NPN, равная широте, вме­сте с тем — высота точки PN, т. е. h_P = φ, или высота повышенного по­люса равна широте места. Рис. "5' удобен для нанесения высот и склонений на меридиане наблюдателя, но неудобен для других задач.

Г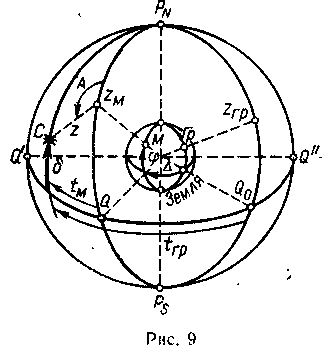еоцентрическое изображение сфе­ры. Для различных наблюдателей на Земле удобнее общее изображение сфе­ры (геоцентрическое). Если поместить центр сферы в центре Земли (см. рис.1, б), а затем повернуть ось мира PNPs вер­тикально, получим изображение сферы, справедливое для любого наблюдателя на Земле (рис. 9). Место наблюдателя М проектируется в точку zм, а его ме­ридиан — в меридиан наблюдателя PNzмPs. Аналогично получаются зени­ты и меридианы других мест, например для Гринвича zгр и PNzrpPs.

Для на­блюдателя М — полуденная точка эк­ватора Q, от нее отсчитываются tM све­тила С, как обычно, к W. Для Гринви­ча имеем точку Q0 и часовой угол tгр. Эта же сфера часто изображается на плоскости экватора (см. рис. 43, 49), где экватор изображается окружностью, а меридиан — прямой (волнистая — по­луночная часть). Из рис. 9 видно, что долгота места равна разности часовых углов

На геоцентрическом изображении сферы нет горизонта, поэтому применяют­ся полярные координаты при zм, т. е. А и z (см. рис. 9). Помимо приведенных изображений сферы, применяют еще изо­бражения ее на плоскости горизонта, первого вертикала (как плоские, так и пространственные): они рассматривают­ся при решении соответствующих задач.

Графическое преобразование ко­ординат на небесной сфере.

Переход от одной системы координат к другим можно выполнить различными путями:

-построением сферы и систем коорди­нат от руки (приближенное графическое решение);

-с помощью моделей сферы: звездного глобуса, планетария, координатных кру­гов;

-аналитическим решением сферических треугольников (с любой степенью точ­ности) .

Рассмотрим графическое решение за­дач.

Построением сферы называется вы­полнение перспективного или плоско­го рисунка ее с нанесением основных линий, точек и координатных систем.

В общем случае удобнее применять ус­ловное перспективное изображение мест­ной сферы на плоскости меридиана на­блюдателя (см. рис, 2).

Меридиан наблюдателя проводят цир­кулем, остальные кривые наносят от руки. При построении сферы примем следующие условия:

-все большие круги сферы, кроме ме­ридиана наблюдателя, изображать эл­липсами;

-полуночную часть меридиана наб­людателя изображать волнистой линией;

-линии на видимой части сферы, т. е. той, где расположено светило, проводить сплошными, а внутри и позади сферы — пунктирными;

-дуги, равные координатам (или их дополнениям), откладывать «на глаз», приблизительно в масштабе основной окружности с точностью до ±5°, как правило, от центра чертежа к его краям.

П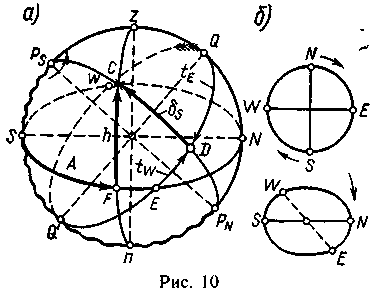орядок построения сферы и преоб­разования координат рассмотрен в при­мере 2. Следует иметь в виду, что гра­фическое решение задач на сфере не исчерпывается задачей преобразования координат. В дальнейшем будут введе­ны движения светил, и графическое при­ближенное решение поможет понять осо­бенности этих движений.

Пример 2. Построить сферу φ = 40° S, нанести светило по t = 295° и δ = 50° S. Определить h и А.

Решение. Проводим окружность R = 4 см. Вертикальный диаметр ее изобразит отвесную линию zn, горизонтальный — полу­денную линию NS (рис. 10). Однако, прежде чем нанести точки N и S, следует определить, какой стороной к наблюдателю должна быть повернута сфера. Указанием служит часовой угол или рассматриваемое явление, например, заход светила — на W-e. Ha рис. 2 сфера по­вернута Е-м к нам, на рис. 4 — W-м. В дан­ном примере t = 295° или t = 65° Е, т. е. светило расположено на E-й половине сферы, и она должна быть повернута к нам Е-м. Мысленно представляя горизонт NESW в виде картушки компаса (рис. 10, б), повора­чиваем ее E к себе, при этом справа будет N, слева S. От точки S откладываем вверх дугу φ = 40° S, получаем повышенный полюс Ps, так как в южной широте над горизонтом бу­дет PS. Проводим ось мира PNPs и получа­ем полуночную часть PsnPN. Перпендику­лярно PNPs проводим экватор QQ', точка Q его расположена на полуденной части меридиана.

Строим изображение горизонта и эква­тора в виде эллипсов, их малые полуоси на­носим с помощью циркуля. В пересечении эл­липсов получаем точки E и W. Линии «внутри» и «позади» сферы делаем пунктирными. На этом рисунок сферы закончен. В заключение следует показать стрелкой при полюсе направ­ление вращения (с Е на W). Координата t в практическом (полукруговом) счете откла­дывается по экватору от точки Q в данном слу­чае к Е. Для удобства отсчета от Е откладыва­ется дуга ED, равная 90°—65° = 25°. Через полученную точку D проводится меридиан PsDPN. По нему от точки D к Ps откладыва­ется δ = 50° S, полученная точка С — ме­сто светила на сфере. Проводя через нее вер­тикал zСn, отмечаем дуги FC и SF, которые равны высоте и азимуту светила. На глаз оцениваем эти координаты и записываем: h = 45°; А = 55° SE; Акр = 125°.

Преобразование координат с помощью моделей сферы. Моделью сферы и не­которых систем координат является при­бор, называемый звездным глобусом. На нем сфера представлена с точки зре­ния наблюдателя, смотрящего на нее снаружи. Звездный глобус может изо­бражать как местную сферу, так и гео­центрическую, если его вынуть из ящи­ка (см. §39).

Глобус имеет координатные сетки, разделенные на градусы, поэтому пре­образование координат осуществляет­ся установкой глобуса и его координат­ных кругов на заданные значения и сня­тием искомых значений координат при­близительно до 1°. Рекомендуется решить пример 2 на звездном глобусе.

Другой имитацией сферы является проекционная установка, называемая планетарием. В нем сфера рассматри­вается изнутри так, как виден небесный свод в натуре. В связи с этим изображе­ния созвездий на глобусе и в планетарии обратны. Планетарий облегчает изуче­ние созвездий и координатных систем, а также позволяет приближенно преобра­зовывать их (до 3°).

Параллактический треугольник и его решение.

Формулы, связывающие координат­ные системы между собой, проще всего получить путем решения сферических треугольников на небесной сфере.

Параллактический треугольник. По­строив сферу для наблюдателя в данной широте и проведя меридиан и вертикал светила С, получим сферический тре­угольник PNZC, в который входят коор­динаты основных систем и географиче­ские координаты места (рис. 11).

Параллактическим треугольником светила называется сферический тре­угольник PNzC, имеющий вершины в повышенном полюсе, зените и месте све­тила и связывающий между собой основ­ные системы сферических координат.

Напомним, что в северной широте по­люс — РN, в южной — Рs.

Элемента­ми этого треугольника, т. е. его сторо­нами и углами, являются:

сторона zPN — дуга меридиана наблюдателя, рав­ная 90° — φ;

сторона PNC — дуга ме­ридиана светила, равная 90° — δ;

сто­рона zC — дуга вертикала светила, рав­ная 90° — h;

угол при зените, равный азимуту светила в полукруговом счете;

угол при повышенном полюсе, равный часовому углу в практическом (полукру­говом) счете;

угол при светиле q — параллактический угол, также в полу­круговом счете.

К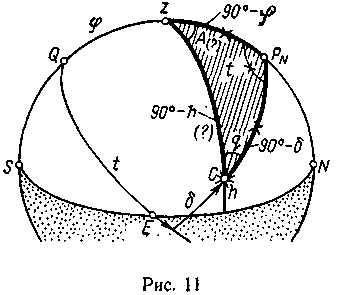ак видим, в треуголь­ник входят полярные координаты, по­этому его иногда называют полярным треугольником светила.

Формулы, связывающие три данных элемента и один искомый элемент сфери­ческого треугольника, называются ос­новными (см. приложение 1.2). В них углы и стороны должны быть меньше 180°. В параллактическом треугольни­ке это достигается использованием полу­кругового счета t, А и q, стороны же всегда меньше 180°. Следовательно, па­раллактический треугольник можно решать по основным формулам сферической тригонометрии.

Особое значение параллактического треугольника, отличающее его от дру­гих, заключается в том, что он связы­вает сферические координаты светила с географическими координатами места наблюдателя. Широта входит в сторону zPN, а долгота — в угол t; это всегда местный часовой угол tм, a по формуле (3) tм=tгр-λw

Поэтому, решая па­раллактический треугольник, по извест­ным координатам светил можно опреде­лить координаты места.

Решение параллактического треу­гольника по основным формулам. Для решения или для построения треуголь­ника РNzС должны быть известны три его элемента. Тогда по основным форму­лам можно определить остальные его эле­менты в общем виде, а затем с помощью таблиц функций или с ЭВМ вычислить эти элементы с нужной точностью.

Треугольник может быть

косоуголь­ным (при произвольном значении его элементов),

прямоугольным (если один или несколько его углов прямые) или

четвертным (при стороне, равной 90°).

Во всех случаях будут справедливы ос­новные формулы, хотя есть и частные формулы и правила для каждого случая. Рекомендуется применять четыре основ­ные формулы сферической тригономет­рии, которые следует знать наизусть (см. приложение 1.2); нужно выучить также формулу пяти элементов, приме­няемую при выводах.