
Вопрос №19
.doc
Вопрос №19.
Суточное движение светил. Изменение горизонтных координат светил в суточном движении. Видимое годовое и суточное движение Солнца, его годовые периоды. Определение места судна по измерениям высот Солнца.
Суточное движение светил.
О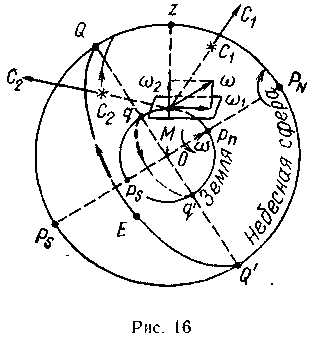 собенности
вращения Земли. Суточное вращение
Земли важно не только для астрономии,
но и в движении спутников, измерении
времени, гироскопии и т. д. Поэтому одна
из главных задач астрометрии -
построение теории ее вращения. Теория
вращения Земли как абсолютно твердого
тела (разработка начата в XVIII
в.) предполагает, что Земля — двухосный
эллипсоид, ее движение - сумма
независимых суточного и годового
движений, причем суточное вполне
определяется силами тяготения Солнца
и Луны. На основании этой теории выявлены
и объяснены:
собенности
вращения Земли. Суточное вращение
Земли важно не только для астрономии,
но и в движении спутников, измерении
времени, гироскопии и т. д. Поэтому одна
из главных задач астрометрии -
построение теории ее вращения. Теория
вращения Земли как абсолютно твердого
тела (разработка начата в XVIII
в.) предполагает, что Земля — двухосный
эллипсоид, ее движение - сумма
независимых суточного и годового
движений, причем суточное вполне
определяется силами тяготения Солнца
и Луны. На основании этой теории выявлены
и объяснены:
скорость вращения Земли относительно оси (с W на Е, ω = 0,000073 рад/с);
движение оси вращения в пространстве (явления прецессии и нутации оси);
движение тела Земли относительно оси вращения — движение полюсов, которое изменяет φ и λ точек на Земле.
Дальнейшее развитие теории вращения Земли, особенно после появления спутников и атомной шкалы времени, привело к учету ее упругости, влияния приливов, наличия и движения атмосферы, внутреннего строения, размещения масс внутри Земли и др. Эти причины сказываются на угловой скорости Земли и движении полюсов. Астрономические и спутниковые наблюдения, особенно в атомной шкале времени, выявили: вековое замедление вращения Земли на (0,00023 с/сут в столетие) и вековое движение полюса (на 0,004" в год по λ= 69°W; в квадрате ≈ 30 м); сезонные колебания суток на ±0,001с (быстрее в июле—августе, медленнее — в марте, в результате за 0,5 года — расхождение с эталоном 0,05с); случайные скачкообразные изменения скорости Земли. Повышение точности измерений приводит к усложнению теории вращения Земли, но без нее невозможно определение по спутникам, которое требует предельной точности по времени и учету мельчайших эффектов.
Вращение горизонта на Земле. Учитывая только вращение Земли с мгновенной скоростью ω (рис. 16), разложим вектор ω для данного наблюдателя М на две составляющие:
ω1 =ωcosφ — горизонтальная составляющая земного вращения — дает наклон плоскости горизонта;
ω2 =ωsinφ — вертикальная составляющая земного вращения — дает поворот горизонта вокруг отвесной линии.
Эти формулы применяются в гироскопии. Они, в частности, позволяют анализировать движение горизонта, например:
в φ = 0° ω1 = ω; ω2 = 0;
в φ = 90° ω1 = 0; ω2 = ω.
Видимое суточное движение светил. Построим около центра Земли О вспомогательную небесную сферу (см. рис. 16) и нанесем на нее линии и точки наблюдателя М и места светил С1, C2.....
Если принять, что Земля и наблюдатель М неподвижны, а небесная сфера вращается в обратном направлении с E на W, то получим ту же картину движения светил, которую видит наблюдатель М в действительности (ему кажется, что Земля и он неподвижны, а светила движутся).
Д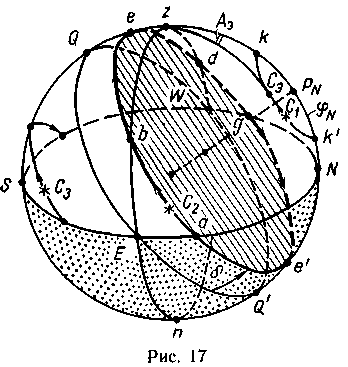 вижение
светил представляем теперь как следствие
суточного вращения сферы и называем
суточным движением светил. Это лишь
кажущееся видимое движение светил
вследствие вращения Земли, но такое
представление удобнее для решения
задач.
вижение
светил представляем теперь как следствие
суточного вращения сферы и называем
суточным движением светил. Это лишь
кажущееся видимое движение светил
вследствие вращения Земли, но такое
представление удобнее для решения
задач.
При суточном вращении сферы отвесная линия, горизонт и меридиан наблюдателя М остаются неподвижными, светила же вместе со сферой движутся. Так как суточное вращение сферы происходит вокруг оси мира PNPs с E на W, то все светила будут описывать малые круги — параллели, плоскости которых перпендикулярны оси мира; они называются суточными параллелями светил. Например, светило С2 (рис. 17) описывает параллель е'е, светило С1 — параллель k'k и т. п. Положение же параллели, как известно, определяется величиной и знаком склонения светила.
Светило в суточном движении занимает ряд характерных положений, например для светила С2 имеем а, Ь, е, d, g, e', которым присвоены названия.
Истинным восходом и заходом светила называются точки пересечения светилом Е и W частей истинного горизонта, например точки параллели a и g. Положением светила на первом вертикале называется пересечение его центром Е или W частей первого вертикала, например в точках параллели b и d.
Кульминацией светила называется пересечение центром светила меридиана наблюдателя. Кульминация называется верхней, если светило пересекает полуденную часть меридиана (наивысшая точка е параллели светила), и нижней, если светило пересекает полуночную часть меридиана (низшая точка е' параллели).
Светило может не пересекать первый вертикал (например, светило С1 на рис. 17), тогда оно дальше всего отходит от меридиана в элонгации.
Элонгацией светила называется такое положение светила, в котором удаление центра его от меридиана наибольшее. Например, проведя вертикал, касательный к параллели k'k, получим точку Сэ восточной элонгации, в которой азимут светила наибольший (Аэ). Кульминации такого светила (верхняя и нижняя) происходят в одном азимуте N или S.
Примечание. Кроме рассмотренной элонгации по азимуту, термин элонгация применяется также к наибольшему удалению на сфере нижней планеты от Солнца, например восточная или западная элонгация Венеры.
Для наблюдателя, находящегося в южной широте, суточное движение происходит аналогично рассмотренному — с Е на W, но полуденная часть меридиана — северная, и движение светил в надгоризонтной части происходит против часовой стрелки (см. рис. 19).
Явления, связанные с суточным движением светил.
У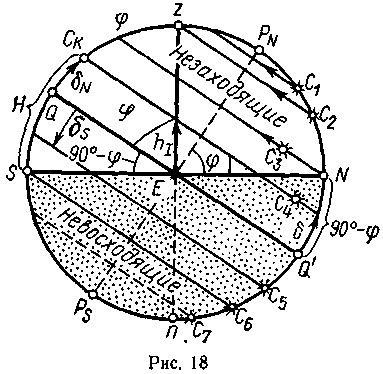 словия
прохождения светилом характерных
точек. Изобразим сферу для наблюдателя
в φN
на плоскости меридиана наблюдателя
и нанесем суточные параллели светил
C1—C7
(рис. 18) с различными склонениями.
словия
прохождения светилом характерных
точек. Изобразим сферу для наблюдателя
в φN
на плоскости меридиана наблюдателя
и нанесем суточные параллели светил
C1—C7
(рис. 18) с различными склонениями.
Часть параллелей пересекает горизонт — эти светила восходят и заходят; другие параллели пересекают первый вертикал или проходят через точки z, N, S и др. Из рис. 18 видно, что положение параллели относительно горизонта определяется соотношением δ и φ.
Условие восхода или захода светила. Чтобы светило пересекало истинный горизонт, его склонение должно быть меньше дуги Q'N или дуги QS. Так, для светила С4 имеем δ < Q'N, для С5 — δ < QS. Но Q'N = QS = 90° — φ.
Следовательно, условием восхода и захода светила в данной широте независимо от наименования δ и φ является неравенство
IδI < 90° - φ (35)
На рис. 18 светила С3 и С5 лишь касаются горизонта в точках N и S. Их параллели являются как бы пограничными: для них δ = 90° - φ. Условием прохождения светила через точку N является δN = 90° - φ; через точку S — δs = 90° - φ.
К северу от параллели С3 расположатся светила, не заходящие в данной широте, для них δ > 90° - φ и одноименно с φ. К югу от параллели С6 расположатся светила, не восходящие в данной широте, т. е. невидимые наблюдателю; для них δ > 90° — φ и разноименно с φ. Например, для Ленинграда φ = 60°N и все светила с δ < 90°—φ = 30° восходят и заходят; светила с δN > 30°, например созвездие Б. Медведицы, находятся всегда над горизонтом (незаходящие); светила с δS> 30°.
Условия пересечения светилом надгоризонтальной части первого вертикала. Из рис. 18 видно, что первый вертикал, который совпадает с линией zn, пересекают те светила, у которых склонение меньше дуги Qz, равной Широте, например светило С4, у которого δ<Qz. Светило С5 также пересекает первый вертикал, так как δ < φ, но в подгоризонтной части. Следовательно, условием пересечения надгоризонтной части первого вертикала является неравенство
δ < φ и одноименно с φ (36)
Светило же С1 для которого δ > φ, не пересекает первый вертикал.
Условие прохождения светила через зенит. На рис. 18 через зенит проходит параллель светила С2, его склонение δ = Qz = φN, наименование δ одноименно с широтой, следовательно, условием прохождения светила через зенит является равенство
δ = φ и одноименно с φ (37)
Через надир светило проходит при δ = φ и разноименных.
Самая южная точка СССР расположена у г. Кушка (φ ≈ 35°10'N), самая северная точка материка — на м. Челюскин (φ ≈ 77°30'N), следовательно, Солнце, а также Луна у нас через зенит проходить не могут, так как наибольшее δ = 23,5°N через зенит у нас проходят только звезды c δ = φN.
Последовательность прохождения видимыми светилами частей горизонта. Восход светила всегда происходит на Е половине сферы, но часть горизонта, где это произойдет, зависит от склонения светила. Рассматривая движение по азимуту, светила можно разделить на три группы:
со склонениями одноименными и большими, чем широта (С1 на рис, 17, 18); они движутся только в двух четвертях (NE, NW — на рис. 17; SE, SW — на рис. 19, б);
со склонениями одноименными, но меньшими, чем широта (С2 на рис. 17); они движутся во всех четырех четвертях: NE, SE, SW, NW;
со склонениями разноименными, но меньшими 90° — φ (С3 на рис. 17); они движутся над горизонтом в двух четвертях (на рис. 17 SE, SW; на рис. 19 NE, NW).
На этом разделении построено правило наименования четвертного азимута, приведенное в МТ—75 (с. 17), применительно к первой и второй системам формул для расчета h и А.
С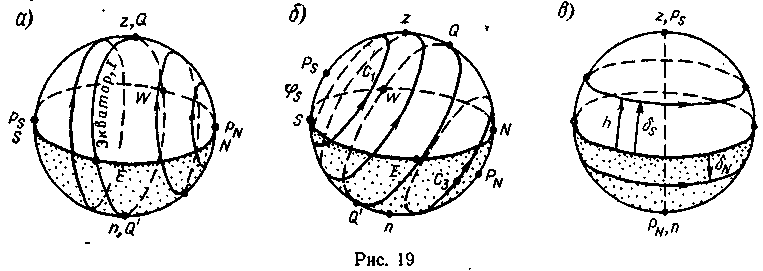 уточное
движение в разных широтах. Положение
суточной параллели светила меняется с
изменением широты места. На рис. 19
видно, как при перемещении наблюдателя
с экватора в среднюю (южную) широту и на
южный полюс постепенно уменьшается
наклон параллелей к горизонту. В φ
= 0° (рис. 19, а) параллели перпендикулярны
горизонту и делятся им пополам: все
светила восходят и заходят, так как δ
< 90°, но ни одно не пересекает первого
вертикала, только светило δ
= 0° движется по первому вертикалу,
который совпадает с экватором. В
промежуточной широте (см. рис. 19, б; φ
= 30°S)
параллели наклонены к горизонту на угол
90° — φ:
часть светил восходит и заходит (δ
< 90° — φ),
есть незаходящие и невосходящие
светила, часть светил пересекает первый
вертикал, одно проходит через зенит
(δ
= φ).
уточное
движение в разных широтах. Положение
суточной параллели светила меняется с
изменением широты места. На рис. 19
видно, как при перемещении наблюдателя
с экватора в среднюю (южную) широту и на
южный полюс постепенно уменьшается
наклон параллелей к горизонту. В φ
= 0° (рис. 19, а) параллели перпендикулярны
горизонту и делятся им пополам: все
светила восходят и заходят, так как δ
< 90°, но ни одно не пересекает первого
вертикала, только светило δ
= 0° движется по первому вертикалу,
который совпадает с экватором. В
промежуточной широте (см. рис. 19, б; φ
= 30°S)
параллели наклонены к горизонту на угол
90° — φ:
часть светил восходит и заходит (δ
< 90° — φ),
есть незаходящие и невосходящие
светила, часть светил пересекает первый
вертикал, одно проходит через зенит
(δ
= φ).
На южном полюсе в φ = 90°S (рис. 19, в) повышенный полюс совпадает с зенитом, горизонт — с экватором, параллели — с альмукантаратами, светила движутся параллельно горизонту, высота h всегда равна δ; светила с δN невидимы, остальные не заходят. Для наблюдателя на полюсе характерно отсутствие меридиана, первого вертикала и точек N, Е, S, W горизонта. Все направления для Ps будут на N, а для РN — на S.
Преобразование координат в частных положениях светил. Вследствие суточного движения положение светила отноcительно горизонта и меридиана наблюдателя непрерывно изменяется. Светило проходит ряд частных положений (см. рис. 17), в которых одна из его координат становится известной. Например, в верхней кульминации (е) часовой угол светил равен нулю, в нижней (е')— 180°, на первом вертикале А = 90°, при истинном восходе h = 0° и т. д. Для частных случаев решение задач на преобразование координат упрощается.
Кульминация светила. В момент верхней кульминации светило находится на меридиане наблюдателя, поэтому его t = 0°; А =180° (0°) и q = 0° (180°).
Светило C4 (см. рис. 18) в верхней кульминации (Ск) имеет меридиональную высоту H, склонение его δN, а дуга QS равна 90° — φ, поэтому формула для меридиональной высоты имеет вид:
H = 90° - φ + δ (38)
Решая эту формулу относительно φ, получим также формулу для определения широты
φ = Z +δ (39)
где Z. и δ приписываются их наименования; если они одноименны, то величины складываются, если разноименны - вычитаются.
Изменение горизонтных координат светил в суточном движении.
Примем, что суточное вращение сферы происходит равномерно (о неравномерностях вращения Земли упоминалось в § 9, учет их показан в § 27), и выясним, какие из координат светил изменяются вследствие суточного движения. Вращение сферы оценивается по смещению какой-либо точки или светила от неподвижного меридиана наблюдателя, т. е. вестовым часовым углом (рис. 20). Поэтому при равномерном вращении сферы часовые углы светил также изменяются равномерно, пропорционально повороту сферы или — приближенно — пропорционально времени. (Изменение часового угла во времени включает еще учет собственного движения светила и движения наблюдателя на Земле (см. § 85). Вследствие этого изменение можно считать пропорциональным времени только за малый промежуток времени.)
Склонение светила
отсчитывается от экватора до параллели,
которая является суточным путем
светила, поэтому в суточном движении δ
не меняется. Прямое восхождение
светила отсчитывается по экватору от
точки Овна, но она связана со сферой
и участвует в ее суточном вращении,
поэтому α
не меняется. Следовательно, в суточном
движении из экваториальных координат
меняются только часовые у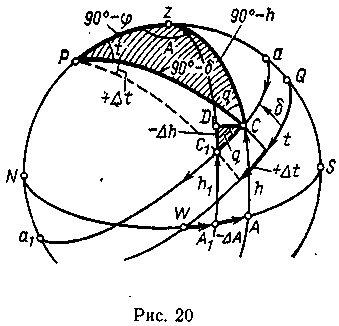 глы;
δ
и α
не меняются; этим объясняется их удобство
для составления звездных карт. Высота
и азимут светила при его движении по
параллели аа1 (см. рис. 20) изменяются.
Вследствие того, что часовой угол
светила меняется равномерно, примем
t
за независимую переменную и найдем
приращения горизонтных координат ∆h
и ∆A
в функции от приращения
∆t
часового угла. Светило С в суточном
движении перемещается по параллели
аа1 и занимает положения С, С1 ... Проводя
меридианы PC
и PC1,
видим, что t
в полукруговом счете изменился на
величину +∆t.
Построив вертикалы zC
и zС1,
видим, что высота изменилась от h
до h1
на величину —∆h,
а азимут в полукруговом счете — на
величину —∆A.
Графический вывод формул изменения
высоты и азимута.
глы;
δ
и α
не меняются; этим объясняется их удобство
для составления звездных карт. Высота
и азимут светила при его движении по
параллели аа1 (см. рис. 20) изменяются.
Вследствие того, что часовой угол
светила меняется равномерно, примем
t
за независимую переменную и найдем
приращения горизонтных координат ∆h
и ∆A
в функции от приращения
∆t
часового угла. Светило С в суточном
движении перемещается по параллели
аа1 и занимает положения С, С1 ... Проводя
меридианы PC
и PC1,
видим, что t
в полукруговом счете изменился на
величину +∆t.
Построив вертикалы zC
и zС1,
видим, что высота изменилась от h
до h1
на величину —∆h,
а азимут в полукруговом счете — на
величину —∆A.
Графический вывод формул изменения
высоты и азимута.
Изменение высоты. Проведя альмукантарат CD на рис. 20, получим на сфере малый ∆CDC1 в котором C1D = —∆h, угол С равен q; гипотенуза CC1 и катет DС1 являются дугами малых кругов, которые меньше соответствующих дуг больших кругов в cos δ и cos h раз (см. приложение 1.1). На этом основании имеем:
![]() и
и
![]()
Принимая ∆CC1D за плоский, найдем C1D:
![]()
или, подставляя вместо CC1 формулу (*), получим
![]()
Заменим δ и q более удобными для анализа координатами, для чего к параллактическому ∆PzC применим формулу синусов:
![]() или
или
![]()
Подставляя это выражение в формулу (40), получим окончательно
![]()
Вследствие сделанных допущений эта формула справедлива только при достаточно малых ∆t; более точную формулу получим ниже с помощью рядов.
Примечание. При круговом счете азимутов и часовых углов формула (41) имеет вид
![]()
где величину sin А надо исследовать на знаки, а ∆t всегда положительно.
Изменение азимута. Из малого ∆CDC1 имеем
![]()
Заменяя CD и СС1 выражениями (**) и (*), получим:
![]() или
или
![]()
Заменим координаты δ и q на горизонтные, для чего в параллактическом ∆РzС (см. рис. 20) применим формулу пяти элементов к углу q:
![]()
После упрощений получим
![]()
Подставляя в выражение (42) вместо cos q cos δ правую часть формулы (43), имеем
![]()
после деления на cos h получим окончательно
![]()
Эта формула справедлива лишь при достаточно малых ∆t.
Примечание. При круговом счете азимутов и t формула (44) имеет знак «+» в северной широте и «—» в южной.
Вывод формул ∆h и ∆A с помощью рядов Тейлора.
Применим ряд Тейлора для отыскания приращений ∆h и ∆A в функции часового угла
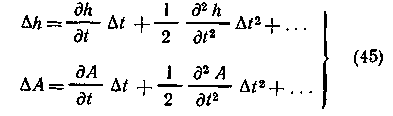
Эти ряды представляют частный случай формул (15), (16) из § 7, причем для ∆А обычно ограничиваются первым членом. Здесь первые производные представляют скорости изменения высоты и азимута в суточном движении (ωh и ωA), а вторые — ускорения. Подставляя их значения в ряды (45), получим
![]()
и
![]()
или, с учетом формулы (43),
![]()
Очевидно, формула (46) представляет уточненную формулу (41), а формула (47) та же, что (44). Ошибки формул обычно оцениваются величиной отброшенных членов ряда (45).
Исследование формулы (46) изменения высоты.
1. Приращение высоты зависит от положения светила по азимуту. Выясним, при каких A высота светила изменяется быстрее. На первом вертикале (A = 90° или 270°) cos A = 0, т. е. ускорение ω’h = 0 и второй член формулы также равен нулю, а скорость ωh = ±cos φ — наибольшая и ∆h = ±cos φ∆t. На меридиане А = 0; 180° скорость ωh = О, ∆h1 = 0, а ускорение — наибольшее и ∆h2 == ±cos φ х cos δ sec Н (∆t2/2)
Следовательно, на первом вертикале высота изменяется быстро и равномерно, в самой кульминации — не меняется, а около — меняется медленно и неравномерно. Практически это означает, что около первого вертикала можно осреднять серии высот за большой ∆t, а около меридиана — за малый ∆t.
2. Приращение высоты зависит от широты места. При φ = 90° имеем ∆h = 0, т. е. на полюсах высоты не меняются. При φ = 0° ∆h может иметь наибольшее значение (при А = 90°), равное изменению часового угла, т. е. ∆h = -∆t. Следовательно, приращение высоты меняется от 0 до ±∆t.
Практическое применение формулы изменения высоты. Выразим в первом члене формулы (46) ∆h в угловых минутах ('), a ∆t— во временных секундах (с). Учитывая, что 1’ — 4c, получим практическую формулу:
![]()
По этой формуле, умноженной на 10, составлена табл. 17 МТ—75. Эти таблицы применяются при контроле серии наблюдений по разностям и при приведении высот к одному моменту. Формула (46) применена также в табл. 2 ВАС—58.
Исследование формул изменения азимута. Установим, на каких участках суточного пути азимут изменяется быстрее. При А = 180° в формуле (47) внутри скобок получится «+», а при A=90 второй член равен нулю. Следовательно, азимут меняется быстрее около верхней кульминации. Отсюда вытекает следствие — для получения наибольшей разности азимутов, например Солнца, его надо наблюдать до и после кульминации (т. е. в φN от SE до SW). Медленнее всего азимут изменяется от восхода до первого вертикала, а в элонгации — не меняется.
Установим, как влияет на ∆А широта места. При φ = 90° ∆А = —∆t, а при φ = 0° ∆А = tg h cos A ∆t (при А = 180° ∆А = tg H ∆t). Следовательно, на экваторе и в тропиках азимут меняется крайне неравномерно — от 0 до мгновенного изменения на 180° (при Н = 90°), а на полюсе — равномерно, так же, как ∆t.
Практическое применение формулы ∆.A В МТ—75 приведена табл. 18 для изменения азимута за 10c времени, рассчитанная по формуле
![]()
умноженной на 10. По этой таблице можно получить скорость изменения азимута ωA, в данный момент. В МТ—63 табл. 15-г дает ∆А° за 1м.
Видимое годовое и суточное движение Солнца, его годовые периоды.
Основные кинематические особенности движения планет были впервые отмечены в законах Кеплера (1571—1630) и затем получили динамическое объяснение и были дополнены Ньютоном (1643—1727) на основе законов механики и закона всемирного тяготения.
Закон всемирного тяготения формулируется так: две материальные частицы взаимно притягиваются с силой F, прямо пропорциональней произведению их масс М и m и обратно пропорциональной квадрату расстоянья г между ними, т. е.
Космические тела в поле тяготения центрального тела, например Солнца, движутся по траекториям, называемым орбитами

![]()
Законы Кеплера.
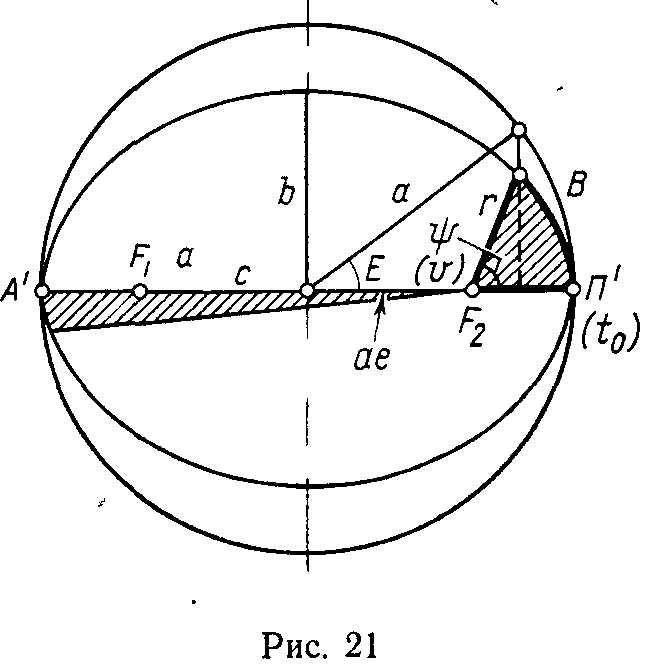
1. Орбиты планет есть эллипсы, в одном из фокусов которых находится Солнце. Радиус-вектор точки эллипса (рис. 21) выражается формулой:
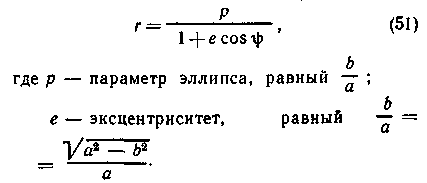
2. Площади, описываемые радиусом-вектором планеты в равные промежутки времени, равны (см. рис. 21)
![]()
где с — момент количества движения точки единичной массы.
Этот закон учитывает неравномерность движения данной планеты по ее орбите: ближе к Солнцу планета движется быстрее, дальше — медленнее.
3. Квадраты звездных периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит. Этот закон показывает, что более близкие к Солнцу планеты имеют большие средние орбитальные скорости, чем более удаленные; например Меркурий имеет v = 48 км/с, Венера —35 км/с, а Плутон — около 5 км/с.
Ньютон показал, что законы Кеплера в общем виде относятся ко всем космическим телам и действуют в любом поле тяготения и что эти законы должны учитывать массы и скорости тел. Формула (51) для радиуса-вектора была выведена Ньютоном из закона всемирного тяготения в общем виде (как уравнение конического сечения с е от 0 до ∞). Из нее следовало, что в центральном поле тяготения орбитами космических тел являются конические сечения: в зависимости от скорости движения тело может описывать эллипс, параболу или гиперболу. Орбитальные скорости определяются из интеграла энергии:
![]()
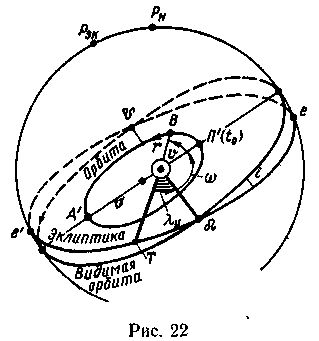
Анализ этой формулы показывает, что:
![]()
![]()
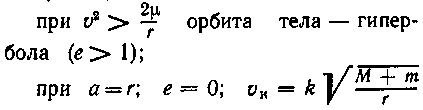
орбита тела — круговая.
Эти закономерности распространяются и на движение искусственных спутников, для которых разделение орбит показано на рис. 40, §21.


П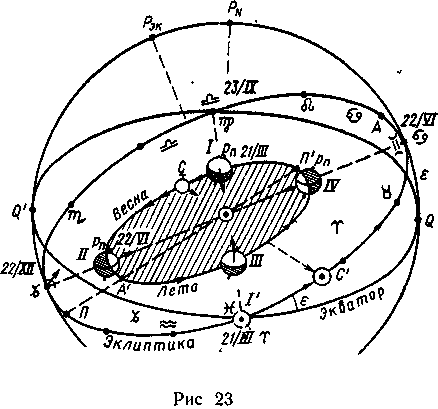 омимо
вращения вокруг оси, Земля, как и все
планеты, обращается по эллиптической
(е = 0,0167) орбите вокруг Солнца (рис. 23) в
направлении суточного вращения,
причем ее ось pnps
наклонена к плоскости орбиты на угол
66°33', сохраняющийся в процессе обращения
(без учета возмущений). Движение Земли
по орбите происходит неравномерно,
что отражено во втором законе Кеплера
(см. § 12). Быстрее всего Земля движется
в перигелии (точка П' на рис. 23), где
v=30,3
км/с, который она проходит около 4 января;
медленнее всего - в афелии (точка А'
на рис. 23), где v
= 29.2 км/с, который она проходит около 4
июля Вследствие этого участки орбиты
///—IV—/
Земля проходит быстрее, а участки
/—II—///
— медленнее. Средняя орбитальная
скорость 29,76 км/с у Земли бывает около
равноденствий (/ и ///). Орбитальное
движение вызывает изменение направлений
на светила для наблюдателя, находящегося
на поверхности Земли. Вследствие
этого положения светил на сфере должны
изменяться, т. е. светила, помимо
суточного движения со сферой, должны
иметь еще и видимые, собственные движения
по сфере
омимо
вращения вокруг оси, Земля, как и все
планеты, обращается по эллиптической
(е = 0,0167) орбите вокруг Солнца (рис. 23) в
направлении суточного вращения,
причем ее ось pnps
наклонена к плоскости орбиты на угол
66°33', сохраняющийся в процессе обращения
(без учета возмущений). Движение Земли
по орбите происходит неравномерно,
что отражено во втором законе Кеплера
(см. § 12). Быстрее всего Земля движется
в перигелии (точка П' на рис. 23), где
v=30,3
км/с, который она проходит около 4 января;
медленнее всего - в афелии (точка А'
на рис. 23), где v
= 29.2 км/с, который она проходит около 4
июля Вследствие этого участки орбиты
///—IV—/
Земля проходит быстрее, а участки
/—II—///
— медленнее. Средняя орбитальная
скорость 29,76 км/с у Земли бывает около
равноденствий (/ и ///). Орбитальное
движение вызывает изменение направлений
на светила для наблюдателя, находящегося
на поверхности Земли. Вследствие
этого положения светил на сфере должны
изменяться, т. е. светила, помимо
суточного движения со сферой, должны
иметь еще и видимые, собственные движения
по сфере
Р
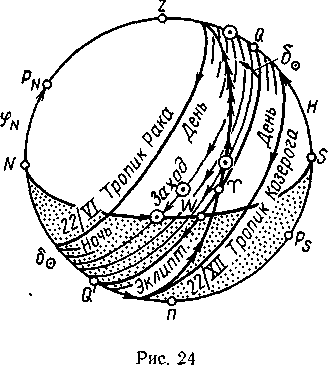 ассмотрим,
как изменяется место Солнца на сфере
вследствие орбитального движения
Земли и связанные с этим явления. Построим
небесную сферу при центре Солнца
(знак его ),
так, чтобы орбита Земли (знак ее ♀)
оказалась внутри сферы (см. рис. 23). С
Земли в положении / Солнце видно в
направлении, показанном стрелкой, и
проектируется на сферу в точку /'. Если
в положении / Земля будет 21 марта, то
точка /' совпадет с точкой Овна (v).
При перемещении Земли в положение С’
наблюдателю на ее поверхности кажется,
что Солнце переместилось по сфере в
положение С' в ту же сторону, что и Земля
по орбите. Это движение Солнца по сфере,
наблюдаемое с Земли в течение года,
называется видимым годовым движением
Солнца; оно происходит в сторону
суточного и орбитального движения
Земли, т. е. является прямым движением.
Из точек //, ///, IV
на орбите Земли Солнце проектируется
на сферу соответственно в точки ,,;
все эти точки лежат на общем большом
круге сферы — эклиптике.
ассмотрим,
как изменяется место Солнца на сфере
вследствие орбитального движения
Земли и связанные с этим явления. Построим
небесную сферу при центре Солнца
(знак его ),
так, чтобы орбита Земли (знак ее ♀)
оказалась внутри сферы (см. рис. 23). С
Земли в положении / Солнце видно в
направлении, показанном стрелкой, и
проектируется на сферу в точку /'. Если
в положении / Земля будет 21 марта, то
точка /' совпадет с точкой Овна (v).
При перемещении Земли в положение С’
наблюдателю на ее поверхности кажется,
что Солнце переместилось по сфере в
положение С' в ту же сторону, что и Земля
по орбите. Это движение Солнца по сфере,
наблюдаемое с Земли в течение года,
называется видимым годовым движением
Солнца; оно происходит в сторону
суточного и орбитального движения
Земли, т. е. является прямым движением.
Из точек //, ///, IV
на орбите Земли Солнце проектируется
на сферу соответственно в точки ,,;
все эти точки лежат на общем большом
круге сферы — эклиптике.
Эклиптикой называется большой круг небесной сферы, по которому происходит видимое годовое движение Солнца. Плоскость этого круга совпадает (или параллельна) с плоскостью орбиты Земли, поэтому эклиптика представляет проекцию орбиты Земли на небесную сферу (точнее проекцию центра тяжести системы Земля—Луна). Эклиптику можно нанести на сферу по координатам Солнца α и δ, как это сделано на звездном глобусе или карте. Выше (см. § 2) было отмечено, что эклиптика, как всякий большой круг, имеет ось Р’экРэк, перпендикулярную плоскости орбиты Земли, полюса эклиптики: северный Рэк и южный Р’эк. Вследствие того что ось Земли pnps сохраняет направление в пространстве, угол е между осью мира РNPs и осью эклиптики РэкР’эк остается приближенно постоянным. На сфере этот угол ε называется наклоном эклиптики к экватору и равен 23°27' (на 1985 г. ε = 23°26,6').
Эклиптика делится экватором на две части: северную и южную. Точки пересечения эклиптики с экватором называются точками равноденствий: весеннего, или мартовского (точка Овна — v), в которой Солнце переходит из южной половины сферы в северную; осеннего, или сентябрьского (точка Весов — ), в которой Солнце переходит из северной в южную половину сферы. Когда Солнце находится в этих точках, его суточная параллель совпадает с экватором и на всем земном шаре, кроме полюсов, день приблизительно равен ночи, отсюда и их название.
Около точек сферы, смещенных относительно равноденствий на 90°, склонение Солнца, равное здесь углу ε. Несколько дней почти не меняется, и Солнце в это время не меняет своей полуденной высоты, т. е. как бы стоит. Отсюда эти точки называются солнцестояниями: летнего, или июньского (точка Рака — ) и зимнего, или декабрьского (точка Козерога — ). Даты прихода Солнца в эти точки и его координаты приведены в табл. 3 и на рис. 23.
Пояс сферы, расположенный на 8° по обе стороны от эклиптики, называется поясом, или кругом Зодиака. Он проходит через 12 созвездий (см. рис. 23) В каждом из этих созвездий Солнце находится около месяца, в соответствии с чем каждому месяцу раньше присваивался знак созвездия.
