9

Вопрос №15.

CНС.

Основные закономерности движения ИСЗ

Для движения ИСЗ по орбите необходимо, чтобы сила земного притяжения была скомпенсирована центробежной силой, возникаю­щей при движении тела вокруг Земли. Это условие приводит к ра­венству

Скорость, при которой начинается движение ИСЗ по окружности во­круг Земли, называется круговой или первой космической скоростью. При H = 0 она равна V1 = V2 = 7,91 км/с.

Период обращения спутника, т. е. время одного его оборота вокруг Земли по круговой орбите радиуса р0,

ИСЗ спутниковых РНС - по орбитам с высо­той порядка 1000 км

периодическими или синхронными спутники - пролетают над за­данными районами Земли ежедневно в одно и то же время.

Синхронный спутник на орбите с высотой Н = 35 870 км имеет Т = 24 ч (точнее — 23 ч 56 мин 4с — одни звездные сутки) и называ­ется суточным. Такие спутники нашли применение в системах связи и телевидения.

Однако ИСЗ двигаются по круговой орбите только в частном слу­чае. В общем случае орбита ИСЗ является эллиптической, имеющей большую а и малую b полуоси. Ближайшая к центру Земли точка ор­биты называется перигеем П (на рис.16.1), наиболее удаленная — апогеем А.

Эллиптическую орбиту характеризуют 6 элементов Кеплера:

-на­клонние i плоскости орбиты плоскости экватора;

-прямое восхождение Ω восходящего узла орбиты;

-угловое расстояние ω перигея от восхо­дящего узла орбиты N1,

-время г прохождения спутника через перигеи или восходящий узел.

Для определения места судна необходимо знать координаты спутника в момент наблюдений, величинами для расчетов являются приведенные выше параметры орбиты.

Орбиты ИСЗ и их особенности

Орбитой спутника называется траектория его движения относи­тельно центра Земли. Плоскость орбиты всегда проходит через центр Земли, классифицируются: в зависимо­сти от наклонения i плоскости орбиты относительно плоскости эква­тора и в зависимости от высоты H орбиты над земной поверхностью. По первому признаку орбиты подразделяются на

экваториальные (i = 0° или 180°), полярные (i = 90°) и наклонные (0° < i < 90°; 90° < i < 180°);

по второму — на низкие (H < 5000 км), средние (5000 < H < 22 000 км), высокие (H > 22 000 км).

зоной радиовидимости (рис.16.2). Сфериче­ский диаметр Θ этой зоны определяется по формуле

(16.5)

Минимальное число ИСЗ для определения места с требуемой дис­кретностью Гтреб может быть определено по формуле

где ∆λmin — минимальная разность долгот на данной параллели, охва­тываемая полосой видимости спутника за один его виток.

Методы omc

дальномерный, радиально-скоростной и разностно-дальномерный.

Дальномерный метод.

параметром - наклонная (топоцентрическая) дальность р до спутника (рис. 16.7). Ей соответствует изоповерхность в виде сферы с центром, совпадающим с ИСЗ, и радиусом, равным измеренной дальности.

Изолиния— окружность сферического радиуса D. Его можно получить из ∆S0ОК:

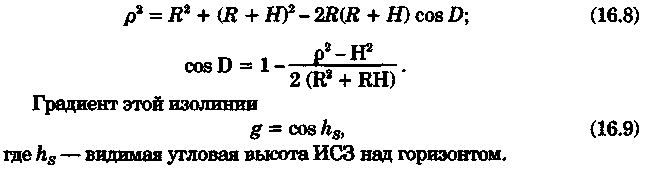
Для определения места необходимо иметь несколько изолиний. Топоцентрическая дальность может быть измерена пассивным или активным методом. Пассивный метод состоит в определении р по вре­мени t распространения радиосигнала от спутника до приемника:

Для измерения дальности р пассивным методом с высокой точностью на спутнике и на судне должны быть высокостабильные генераторы частоты.

Активный метод измерения дальности до спутника аналогичен методу измерения расстояния до активного радиолокационного от­ражателя

Этот метод не требует наличия высокостабильных генераторов частоты на судне. Но при его ис­пользовании возникает другая проблема — обеспечение одно­временного обслуживания сотен и тысяч потребителей.

Радиально-скоростной метод. - метод определения места, основанный на измерении скорости сближения спутника с наблюдателем, применяется эффект Доплера (что при быстром перемещении спутника, излучающего колеба­ния частоты f0, наблюдатель будет принимать колебания другой частоты f ). Разность этих колебаний, называемая доплеровским смещением частоты:

Входящая в формулу (16.10) величина vcos a = vp называется ра­диальной скоростью.

Разностно-дальномерный метод.

Этот метод основан на из­мерении разности топоцентрических расстояний между судном и двумя положениями одного и того же ИСЗ в последовательные мо­менты времени.

Вопрос №16.

РЛС и САРП

На морских судах применяются ИКО с двумя видами изображения обстановки: в отно­сительном движении (ОД); в истинном движении (ИД).

Изображение ориентировано: относительно (ДП) («по курсу»); относительно гирокомпасного меридиана («по норду»).

Основные эксплуатационные данные РЛС

Радиоволны сантиметрового диапазона, которые распространяются и отражаются по законам све­товых волн с несколько большим коэффициентом рефракции. Дальность действия радиолокатора:

Др – дальность р-л горизонта, h_{Д -} действующая высота антенны.

Дальность обнаружения отдельных объектов с помощью РЛС мо­жет быть определена по формуле

Ширина диаграммы направ­ленности антенны РЛС в вертикальной плоскости обычно 15...30°, Пространство ниже этой кромки называется мертвой зоной.

величина мёртвой зоны определяется радиусом окружности

где а — ширина диаграммы направленности в вертикальной плоскости.

нужно определять и экспериментально, используя в качестве надводного объекта шлюпку.

Разрешающая способность РЛС может быть охаракте­ризована площадью разрешения, под которой подразумевают пло­щадь, занимаемую изображением на экране эхо-сигнала точечного объекта. Изображение эхо-сигнала такого объекта имеет вид дуто-. образной полоски, ширина которой в масштабе экрана соответству­ет линейной ширине луча на расстоянии объекта; длина (радиаль­ная) соответствует расстоянию в масштабе экрана, которое прохо­дят радиоволны за время, равное длительности импульса,

Точность радиолокационного пеленгования.

зависит от следующих факторов:

ширины диаграммы направленности в горизонтальной плос­кости (m1); неточной центровки начала развертки (m2); неточного визирования эхо-сигнала объекта (m3); погрешности нуля отсчета, вызванной сдвигом антенны относи­тельно ДП судна или относительно гироскопического меридиана (m4); инструментальной погрешности передачи на индикатор угла вращения антенны (m5); погрешности параллактического характера (m6).

Радиолокационная девиация. мачты, такелаж, антенны и другие устройства - теневые секторы ,отсчеты РЛП, взятые в этих секторах и в пределах 3...5° от их границ могут содержать значительные погрешности, называемые радиолокацион­ной девиацией учтена как поправка при расчете радиолокационного пе­ленга:

Затем составляют таблицу р-девиации как функции РЛКУ.

Точность измерения расстояний. Расстояние до эхо-сигнала объекта на экране РЛС может быть измерено с помощью не­подвижных (НКД) и подвижных (ПКД) кругов дальности - приближенно, путем глазомерной (расстояние между НКД с точностью до 1/10, - погрешность в ±10% от этого расстояния).

Погрешность калибровки (каждое фик­сированное значение радиуса подвижного круга не соответствует действительному расстоянию для избранного масштаба). При ка­либровке ПКД расстояния, измеренные с помощью РЛС, сравни­вают с расстояниями, измеренными геодезическим путем (остаточная погрешность не бу­дет превышать 10 м).

Инструментальная погрешность вызывается неточностью работы фазовращателя РДС и обычно имеет величину примерно ± 10... 15 м.

Случайная погрешность - зависит от опыта наблюдателя, четкости и масштаба изображения объекта и может быть выведена из серии отсчетов.

Погрешность объекта ( наиболее существенной). Штурман не всегда может точно указать на карте ту часть объекта, ко­торая создала передний фронт эхо-сигнала на ИКО.

Точность измерения расстояний с помощью РЛС, определенная экспериментальным путем, приводится в описании каждой станции и колеблется в пределах 0,2...1,0кб. На качке погрешность измере­ния расстояний несколько возрастает, но погрешность не превышает высоты антенны.

Чтение радиолокационного изображения

Искажение линии берегов.

Изображение берега на ИКО во многих случаях может значительно отличаться от карты:

оно соответствует не урезу воды, а некоторой приподнятой час­ти суши + экранирующие объекты (остров, гора и т. п.).

Влияние морского волнения.

Эхо-сигналы, м создавать в центре экрана ятно радиусом до 2 миль, в шторм — до 4 миль. Засветка, создаваемая волнением. Можно снизить, уменьшая чувствительность.

Влияние метеорологических условий.

При некоторых условиях может наблюдаться аномальное распро­странение радиоволн сантиметрового диапазона, связанное с изме­нением коэффициента рефракции. При нормальном состоянии (рис. 17.10,а). Если коэффициент атмосферной рефрак­ции убывает с высотой со скоростью меньше нормальной, или увели­чивается, при этом лепесток диаграммы направленности РЛС будет поднят выше над поверхностью моря, что приведет к уменьшению дальности радиолокационного горизонта (рис. 17.10,b) - пониженной рефракцией (субрефракцией). Оно воз­никает, когда холодный влажный воздух распространяется над теп­лой водой. Если ------ больше нормальной, (рис. 17.10, в - повышенной рефракцией (сверхрефракцией). До нескольких сотен миль.

Обнаружение льдов.

лед обладает малой эффективной площадью отражения.

Ровный, гладкий лед почти не виден на экране РЛС.

Теневые секторы.

Чтобы обнаружить суда и другие объекты, оказавшиеся в теневых секторах, нужно периодически на короткое время

Вопрос №17.

Небесная сфера. Системы сферических координат….

Небесная сфера.

вспомо­гательная сфера произвольного радиуса, к центру которой параллельно перене­сены основные линии и плоскости на­блюдателя Земли и направления на светила.

вертикаль, или отвесная линия, z01 (см. рис. 1) географической широтой φ и долготой λ

—зенитом z и надиром n. ось мира PNPs, полюсами мира. истинный горизонт. небесный экватор — большой круг QWQ'E. меридиан наблюда­теля— большой круг PNzQPsQ'. Ось мира PNPS разделяет меридиан наблю­дателя на полуденную часть PNzPs, включающую зенит, и полуночную PNnPs

Полюс мира, расположенный над го­ризонтом, называется повышенным по­люсом. Возвышение полюса над горизонтом, т. е. дуга NPN, равно широте, так же как дуга zQ (см. рис. 2).

Спроектированная плоскость орбиты Земли даст эклиптику

Системы вспомогательных кругов.

Круги, связанные с отвесной линией:

верти­калы, альмукантараты, не­бесные меридианы, параллели

Системы сферических координат, используемые в мореходной астрономии.

Горизонтная система координат.

Основными кругами (осями координат) в этой системе являются –

истинный го­ризонт и меридиан наблюдателя:

основ­ным направлением - отвесная линия zn

Положение точки или светила на сфере определяется двумя координата­ми: высотой и азимутом (рис. 4, сфера на нем для φN повернута W-м к зрите­лю)

Азимутом А светила называется дуга истинного горизонта между мери­дианом наблюдателя и вертикалом све­тила

Полукруговой азимут считается в пределах О—180° от полуночной части ме­ридиана наблюдателя в сторону Е или W до вертикала светила

Круговой азимут. Четвертый азимут

Полярные координаты. Зенит является полюсом, а меридиан наблюдателя — полярной осью координат A и z. Азимут в полярных координатах определяется как угол при зените в полукруговом сче­те (см. рис. 4).

Зенитным расстоянием z называется дуга вертикала от зенита до места свети­ла в пределах О—180°

Меридиональная высота H - высота све­тила, расположенного на меридиане на­блюдателя.

Первая экваториальная система ко­ординат.

Основным направлением в этой системе является: ось мира PNPs,

основными кругами: экватор и меридиан наблюдателя.

Положение точки на сфере определяется двумя координата­ми: склонением и часовым углом (рис. 5).

Склонением δ светила называется ду­га меридиана светила от небесного эква­тора до места светила. Склонения считаются от О до 90° к N или S; например, на рис. 5 для светил С1 и С2 имеем δ1 = 33°N, δ2 =26S.

Часовым углом t называется дуга эк­ватора от полуденной части меридиана наблюдателя до меридиана светила, счи­таемая в сторону точки W от 0 до 360°. Дуга экватора QD из­меряет центральный угол t или сфериче­ский угол при полюсе t, которые также называют часовыми углами.

Полярным расстоянием ∆ называется дуга меридиана светила от повышен­ного полюса до места светила, считае­мая oт 0 до 180°, например для светила С1 ∆ =57°

Вторая экваториальная система ко­ординат.

В этой системе основное на­правление-ось мира,

а основными кру­гами являются-небесный экватор и ме­ридиан точки Овна (γ).

Точка Овна, или точка весеннего равноденствия, рас­положена в пересечении экватора с эк­липтикой, т. е. связана с орбитой Зем­ли.

Положение светила в этой системе определяется-склонением и прямым вос­хождением (рис. 6).

Склонение δ в этой системе аналогично первой экваториаль­ной системе.

Прямым восхождением α светила на­зывается дуга экватора от точки Овна до меридиана светила, считаемая в сто­рону, обратную W часовым углам (т. е. в сторону Е) от 0 до 360°. звездное дополнение: (т=360- α)

Звездным дополнением т называют дугу экватора от точки Овна до меридиа­на светила, но считаемую в сторону W часовых углов

Полярные координаты. α (или т) ∆

Первая и вторая экваториальные си­стемы отличаются только положением начального меридиана: t считается от точки Q, а α — от точки Овна (v), по­ложение же точки Овна определяется ее часовым углом t^v, поэтому (см. рис.6)

т. е. часовой угол точки Овна (звездное время) равен сумме часового угла и прямого восхождения светила. По этой формуле (в § 23 она названа основной формулой времени) можно перейти от одной системы к другой.

Эклиптическая система координат.

В этой системе основным направлением является-ось эклиптики,

а основными кругами -эклиптика (плоскость орби­ты Земли) и круг широты точки Овна (рис. 7).

Ось-полюсах эклиптики — северном РЭК и южном Р’ЭК. Большие круги-полюса эклиптики, на­зываются кругами широты (см. рис. 7).

Эклиптической широтой β называет­ся дуга круга широт от эклиптики до места светила в пределах 0—90° со зна­ком «+» к северу, «—» к югу.

Эклиптической долготой λ называется дуга эклиптики от точки Овна до кру­га широты светила — от 0 до 360° в сторону счета α.

Связь с географическими координатами.

Связь широты наблюдателя с коор­динатами точек сферы. применить плоское изобра­жение сферы

Из рис. 8 видно, что широте равны еще три дуги, остальные равны 90° - φ. Дуга NPN, равная широте, вме­сте с тем — высота точки PN, т. е. h_P = φ, или высота повышенного по­люса равна широте места. Рис. "8' удобен для нанесения высот и склонений на меридиане наблюдателя, но неудобен для других задач.

Геоцентрическое изображение сфе­ры. Если поместить центр сферы в центре Земли (см. рис.1, б), а затем повернуть ось мира PNPs вер­тикально, получим изображение сферы, справедливое для любого наблюдателя на Земле (рис. 9). Место наблюдателя М проектируется в точку zм, а его ме­ридиан — в меридиан наблюдателя PNzмPs. Аналогично получаются зени­ты и меридианы других мест, например для Гринвича zгр и PNzrpPs.

Для на­блюдателя М — полуденная точка эк­ватора Q, от нее отсчитываются tM све­тила С, как обычно, к W. Для Гринви­ча имеем точку Q0 и часовой угол tгр.

Вопрос №18.

Измерение времени. Звездное и солнечное времена…

Измерение времени.

Для изме­рения времени используются следующие периодические процессы:

-суточное вращение Земли (или небес­ной сферы);

-годичное обращение Земли вокруг Солнца (или годичное движение Солн­ца);

-частоты излучения или поглощения молекул или атомов.

Сутками называется промежуток вре­мени, за который Земля (или небесная сфера) делает один оборот вокруг оси. В зависимости от того, по какой точке сферы замечается ее оборот, различают звездные сутки (по точке Овна), истин­ные солнечные и средние солнечные сут­ки (по «среднему» Солнцу).

Звездные и средние сутки делятся на часы, мину­ты и секунды в них длительность основ­ной единицы — секунды—различна. За основу была принята средняя солнечная секунда затем-эфемеридная секунда- «атом­ная секунда» и является эталонной, при­ближающейся к эфемеридной.

Для измерения промежутка времени удобнее измерять другую физическую величину — угол поворота сферы за про­текшее время, т. е. часовой угол данной точки. При этом часовой угол точки Ов­на (рис. 42) называется звездным вре­менем, а угол поворота среднего Солнца от полуночи (от точки Q', см. рис. 42)— средним временем.

Системы счета времени определяются тем, от какого меридиана и в каких еди­ницах ведется счет. Если считать от меридиана данного места, получим мест­ное время — звездное (SМ) или среднее (Тм), на гринвичском — гринвичское (звездное и среднее). В повседневной жизни применяется только среднее сол­нечное время в системах поясных, де­кретных, судовых и других времен. В качестве эталонной системы применяет­ся гринвичское среднее время, выражен­ное в атомных секундах, — это всемир­ное координированное время (UTC)