
- •1.Основные понятия теории алгоритмов.
- •2.Примитивно рекурсивные функции. Базис элементарных функций. Операции подстановки и примитивной рекурсии.
- •3.Примитивно рекурсивные функции. Основные свойства операций подстановки и примитивной рекурсии.
- •4.Примитивно рекурсивные функции относительно совокупности функций. Основные свойства.
- •5.Производные операции над функциями.
- •6.Операции конечного суммирования и конечного произведения.
- •7.Предикат, логическая функция. Логические операции с предикатами.
- •8.Операции навешивания кванторов. Операции навешивания кванторов относительно двуместных предикатов
- •9.Примитивно рекурсивный предикат.
- •10. Операция навешивания ограниченного квантора над предикатами
- •11. Кусочное задание функции.
- •12 Операция ограниченной минимизации.
- •13.Частично рекурсивные функции.
- •14. Машина Тьюринга (мт). Применение мт к словам
- •16. Вычислимые по Тьюрингу функции.
- •17. Правильная вычислимость функций на машине Тьюринга.
- •18. Вычислимость по Тьюрингу примитивно рекурсивных функций. Суперпозиция.
- •19. Вычислимость по Тьюрингу примитивно рекурсивных функций. Примитивная рекурсия.
- •20. Вычислимость по Тьюрингу частично рекурсивных функций.
- •22. Нормальные алгоритмы Маркова и их применение к словам.
- •23. Нормально вычислимые функции и принцип нормализации Маркова.
- •15.Конструирование мт. Операции над машинами Тьюринга.
11. Кусочное задание функции.
Пусть
задана совокупность функций
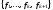 и совокупность предикатов
и совокупность предикатов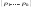 ,
где
,
где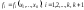 и
и ,
причем области истинности предикатов
попарно не пересекаются.
,
причем области истинности предикатов
попарно не пересекаются.
Введем
следующие обозначения:
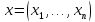 .
.
Определение.
Говорят, что функция
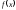 задана кусочным образом относительно
заданной совокупности функций и
предикатов, если она удовлетворяет
следующим условиям:
задана кусочным образом относительно
заданной совокупности функций и
предикатов, если она удовлетворяет
следующим условиям:
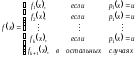 ,
,
Теорема
4. Функция
f(x),
заданная кусочным образом из совокупности
 ,
является ПРФ относительно ψ
,
является ПРФ относительно ψ
Доказательство.
Пусть
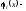 представляющая функция для предикатаpi(x),
где
представляющая функция для предикатаpi(x),
где
 .
Тогда покажем, что функциюf(x)
можно представить следующим образом
.
Тогда покажем, что функциюf(x)
можно представить следующим образом
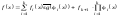 .
(32)
.
(32)
Рассмотрим произвольный набор
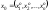 .
.
Пусть
для какого – то
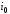 предикат
предикат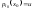 ,
где
,
где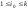 . Тогда по определению представляющей
функции предиката, получаем, что
. Тогда по определению представляющей
функции предиката, получаем, что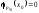 ,
следовательно
,
следовательно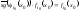
а для всех остальных ii0 , pi(x0)=л, отсюда
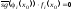 .
.
Таким образом, в данном случае, мы получаем, что
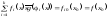 .
.
Предположим, что для любого i,
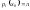 ,
тогда
,
тогда ,
где
,
где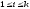 .
Следовательно,
.
Следовательно,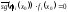 ,
а
,
а
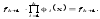
Из
пунктов 1–2 следует, что на множестве
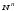 функция
функция
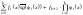
совпадает
с функцией
 ,
которая задана кусочным образом из
совокупности ψ. Так как операции
конечного суммирования и конечного
произведения сохраняют свойством
примитивно рекурсивности функций,
следовательно, рассматриваемая функция
является ПРФ относительно ψ. Ч.т.д.
,
которая задана кусочным образом из
совокупности ψ. Так как операции
конечного суммирования и конечного
произведения сохраняют свойством
примитивно рекурсивности функций,
следовательно, рассматриваемая функция
является ПРФ относительно ψ. Ч.т.д.
Лемма 1.1. Подстановка примитивно рекурсивной функции в предикат равенства есть примитивно рекурсивный предикат.
Доказательство. Пусть
заданы примитивно рекурсивные функции
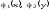 и пусть
и пусть –
предикат равенства.
–
предикат равенства.
Рассмотрим
предикат вида
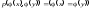 .
.
Он
является примитивно рекурсивным
предикатом. Действительно, для данного
предиката представляющей функцией
является функция вида
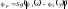 ,
,
которая является ПРФ.
12 Операция ограниченной минимизации.
Пусть
задан всюду определенный предикат
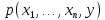 .
.
Определение.
Говорят, что функция
 получена из предиката
получена из предиката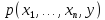 в результате
операции ограниченной минимизации,
т.е.
в результате
операции ограниченной минимизации,
т.е.
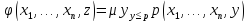 ,
если выполняется следующие равенства.
,
если выполняется следующие равенства.
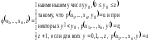
Действительно эта равенства имеет место.
Пусть
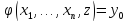 ,
тогда
,
тогда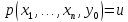 и для всехy<y0
и для всехy<y0
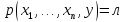 .
.
Следовательно
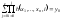 .
.
Пусть,
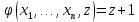 .
Тогда по определению операции
ограниченной минимизации
.
Тогда по определению операции
ограниченной минимизации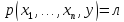 для всехy,
где
для всехy,
где
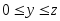 .
Следовательно, в правая часть формуле
(1), равна z+1
единиц.
.
Следовательно, в правая часть формуле
(1), равна z+1
единиц.
Таким
образом, из пунктов 1–2 следует, что
формула (34) удовлетворяет заданию
функции с помощью операции ограниченной
минимизации. Так как операции конечного
произведения и конечного суммирования
сохраняют свойства примитивной
рекурсивности функцией, то получаем,
что функция
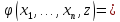 является ПРФ относительно
является ПРФ относительно .
.
Следствие. Операция ограниченной минимизации сохраняет свойство примитивной рекурсивности функций.
13.Частично рекурсивные функции.
Пусть
задана функция
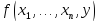 .
.
Определение.
Говорят, что
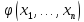 .
получено из
.
получено из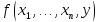 с применением
операции ограниченной минимизации,
если имеет место следующее равенство:
с применением
операции ограниченной минимизации,
если имеет место следующее равенство: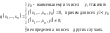 (44)
(44)
и
обозначают
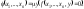 (45)
(45)
Лемма 1.2. Операция ограниченной минимизации сохраняет свойство примитивной рекурсивности функции.
Действительно,
если имеется алгоритм ,
вычисляющий функции
,
вычисляющий функции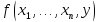 ,
то есть и алгоритм
,
то есть и алгоритм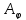 вычисляющий функции
вычисляющий функции ..
..
Доказательство.
Пусть
требуется вычислить значение функции
на произвольном наборе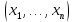 .
.
1шаг. Применим
алгоритм
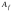 к набору
к набору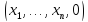 .
Если через конечное число шагов алгоритм
завершает свою работу результативно,
т.е. вычислено значение
.
Если через конечное число шагов алгоритм
завершает свою работу результативно,
т.е. вычислено значение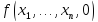 и
и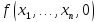 =0,
то значение функции
=0,
то значение функции на наборе
на наборе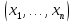 .
считаем равным 0. Если
.
считаем равным 0. Если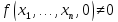 ,
то переходим к следующему этапу, на
котором применяем алгоритм
,
то переходим к следующему этапу, на
котором применяем алгоритм к набору
к набору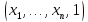 .
.
Если через конечное
число шагов алгоритм завершает свою
работу на данном наборе результативно,
т.е. вычислено значение
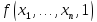 и
и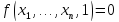 ,
то значение функции
,
то значение функции на наборе
на наборе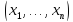 .
считаем равным 1. Если
.
считаем равным 1. Если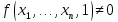 ,
то переходим к следующему этапу и т.д.
,
то переходим к следующему этапу и т.д.
Если на (t+1)
шаге вычислено значение
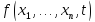 и
и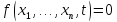 ,
то значение функции φ на наборе
,
то значение функции φ на наборе .
считаем равнымt.
Если
.
считаем равнымt.
Если
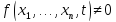 ,
то переходим к следующему этапу.
,
то переходим к следующему этапу.
В случае, когда
алгоритм
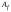 завершает свою работу на каком-то этапе
безрезультативно, или работает
бесконечно, то будем считать, что
значение
не определено на данном наборе, т.е. на
наборе
завершает свою работу на каком-то этапе
безрезультативно, или работает
бесконечно, то будем считать, что
значение
не определено на данном наборе, т.е. на
наборе
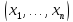 .
.
Определение.
Частично рекурсивным описанием (ЧРО)
функции f
называется конечная последовательность
функций
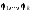 ,
удовлетворяющих следующим условиям:
,
удовлетворяющих следующим условиям:
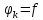 ;
;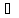 i
i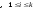 ,
,
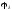 – яв-ся либо элемент-й функцией, либо
получается из предшествующей ей
последовательности функций с помощью
одной из операций: подстановки,
примитивной рекурсии или ограниченной
минимизации.
– яв-ся либо элемент-й функцией, либо
получается из предшествующей ей
последовательности функций с помощью
одной из операций: подстановки,
примитивной рекурсии или ограниченной
минимизации.
Определение. Функция f называется ЧРФ, если существует ее ЧРО.
Определение. Функция f называется общерекурсивной, если она ЧРФ и всюду определена. (В других источниках такие функции называются тотальными или просто рекурсивными.)
каждая примитивно рекурсивная функция является частично рекурсивной, но обратное неверно.
Введем обозначения:
KПРФ – класс примитивно рекурсивных функций;
KОРФ – класс общерекурсивных функций;
KЧРФ – класс частично рекурсивных функций.
Тогда между этими классами имеется соотношения:
KПРФ KОРФ
KОРФ KЧРФ.
KЧРФ.
Таким образом,
класс ЧРФ – самый богатый из построенных
классов вычислимых функций и имеет
место следующее включение: KЧРФ КВФ,
КВФ,
где КВФ – класс вычислимых функций.
Тезис
Черча–Клини представляет гипотезу,
из которой следует обратное включение,
т.е. КВФ KЧРФ.
KЧРФ.
Таким образом, класс алгоритмически вычислимых функций совпадает с классом частично рекурсивных функций.
