4.Примитивно рекурсивные функции относительно совокупности функций. Основные свойства.

Пусть задана последовательность ф-ий ).

Определение. Примитивно рекурсивное описание (ПРО) функции f относительно совокупности ψ называется конечная последовательность функций вида ), удовлетворяющая следующим условиям:

1. .

2. Для любого i=1,…,n, – есть либо элементарная функция, либо ψ, либо получается из предшествующих ей функций в этой последовательности с помощью одной из операций примитивной рекурсии или подстановки.

Определение. Функция f называется ПРФ относительно совокупности ψ, если существует ее ПРО относительно совокупности ψ.

Осн. свойства ПРФ относительно совокупности ψ.

1⁰. Если функция f – ПРФ относительно совокупности 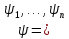), и ψc Г, то функция f, также является ПРФ относительно совокупности функций из Г. (где Г– множество, включающее произвольные арифметические функции).

Доказательство. Пусть функция f ПРФ относительно совокупности ). Тогда существует ее ПРО относительно совокупностиψ, т.е. 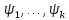. Если, то в силу того что ψc Г, . Следовательно, ПРО функцииf относительно совокупности ψ является и ПРО функции f относительно совокупности Г. Отсюда следует, что f есть ПРФ относительно Г. ч.т.д.

2⁰. Если f ПРФ относительно совокупности иполучается из ψ при удалении какой – то функции(где- ПРФ), т.е., то функцияf будет также ПРФ относительно совокупности .

3⁰. Если f – ПРФ относительно совокупности ) и каждая функция из ψ есть ПРФ относительно Г, тоf является ПРФ относительно Г.

Доказательство. Доказательство аналогично доказательству свойства 2⁰. Рассмотрим ПРО функции f относительно совокупности ψ, т.е. . Каждая функция, гдеi=1,…,k принадлежит совокупности ψ. Так как каждая функция совокупности ψ является ПРФ, то некоторые из них заменим на ПРО относительно Г. Таким образом, образуем ПРО функции f относительно Г. Следовательно функция f–ПРФ относительно совокупности Г.

4⁰. Если f– ПРФ относительно совокупности ), и каждая функция из совокупности ψ, есть ПРФ, тоf тоже является ПРФ.

5.Производные операции над функциями.

1.)Пусть задана некоторая функция g(x,y) и функция φ(x,y,z)=g(x,y).

Говорят, что функция φ получена из функции g с помощью операции введения фиктивной переем-й ().

При этом функция φ(x,y,z) является ПРФ относительно совокупности . Действительно,φ можно представить следующим образом:

φ(x,y,z)=g(,).

Как видим, функция φ получена из функции g и операцией подстановки, т.е..

2. Пусть задана функция g(x,y,z) и если φ(x,y)=g(x,y,a), то говорят, что функция φ получена из функции g с помощью операции замены константы.

Действительно φ(x,y) можно представить следующим образом:

и называется операция замены константы.

3. Пусть задана функция g(x,y) и φ(x,y)=g(x,y), то говорят, что функция φ получена из функции g с применением операции перестановки переменных. Действительно функцию φ(x,y) можно представить следующим образом:

φ(x,y)= .

4) Пусть дана функция g(x) и φ(x)=g(x,x), то говорят, что функция φ получена из функции g с помощью операции отождествленной переменной.

Действительно, функцию φ можно представить следующим образом:

т.е. .

5.) Пусть заданы функции , где– некоторые функции различного количества переменных. Если, то говорят, что функцияφ получена из функции g с помощью операции произвольной подстановки (суперпозиции).

Определение. Операция F называется примитивно рекурсивной операцией, если из равенства φ=F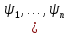) следует, что функция φ есть ПРФ относительно совокупности ψ.

Рассмотрим пример.

Пусть задана функция g(x,y) и функция φ(x,y,z)=g(x,y).

Функция φ получена из функции g с помощью операции введения фиктивной переменной.

При этом функция φ(x,y,z) является ПРФ относительно совокупности {g}.

Действительно, φ можно представить следующим образом: φ(x,y,z)=g(,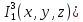)..Как видим, функция φ получена из функции g и операцией подстановки, т.е..