
- •1.Основные понятия теории алгоритмов.
- •2.Примитивно рекурсивные функции. Базис элементарных функций. Операции подстановки и примитивной рекурсии.
- •3.Примитивно рекурсивные функции. Основные свойства операций подстановки и примитивной рекурсии.
- •4.Примитивно рекурсивные функции относительно совокупности функций. Основные свойства.
- •5.Производные операции над функциями.
- •6.Операции конечного суммирования и конечного произведения.
- •7.Предикат, логическая функция. Логические операции с предикатами.
- •8.Операции навешивания кванторов. Операции навешивания кванторов относительно двуместных предикатов
- •9.Примитивно рекурсивный предикат.
- •10. Операция навешивания ограниченного квантора над предикатами
- •11. Кусочное задание функции.
- •12 Операция ограниченной минимизации.
- •13.Частично рекурсивные функции.
- •14. Машина Тьюринга (мт). Применение мт к словам
- •16. Вычислимые по Тьюрингу функции.
- •17. Правильная вычислимость функций на машине Тьюринга.
- •18. Вычислимость по Тьюрингу примитивно рекурсивных функций. Суперпозиция.
- •19. Вычислимость по Тьюрингу примитивно рекурсивных функций. Примитивная рекурсия.
- •20. Вычислимость по Тьюрингу частично рекурсивных функций.
- •22. Нормальные алгоритмы Маркова и их применение к словам.
- •23. Нормально вычислимые функции и принцип нормализации Маркова.
- •15.Конструирование мт. Операции над машинами Тьюринга.
3.Примитивно рекурсивные функции. Основные свойства операций подстановки и примитивной рекурсии.
Основные свойства операции подстановки
10.Операция подстановки сохраняет свойство всюду определенности функций, т.е. если функция
 и функции
и функции
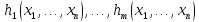
всюду определенные
функции и функция f
получается из них с помощью операции
подстановки f=S(g,,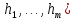 ,
,
то f также является всюду определенной функции.
Доказательство.
Пусть
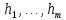 произв-е ф-ии отn
переменных.
произв-е ф-ии отn
переменных.
Рассмотрим
произвольный набор
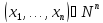 .
.
Тогда
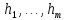 будут определены в этом наборе в силу
свойства всюду определенности.
будут определены в этом наборе в силу
свойства всюду определенности.
Функция g
будет определена на наборе
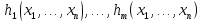 ,
в силу свойства всюду определенности,
а по определению подстановки это и есть
функцияf.
,
в силу свойства всюду определенности,
а по определению подстановки это и есть
функцияf.
Таким
образом, мы доказали, что функция f
определена на наборе
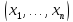 .
.
Так как, мы взяли произвольный набор из множества натуральных чисел, то свойство доказано.
20. Операция подстановки сохраняет свойство алгоритмической вычислимости функций:
если функции
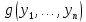 и
и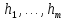 алгоритмически вычислимы, и
алгоритмически вычислимы, и
f=S(g,,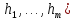 ,
то существует алгоритмAf,
вычисляющий функцию f.
,
то существует алгоритмAf,
вычисляющий функцию f.
Доказательство.
Пусть задан произвольный набор
![]() .
Это означает, что этот набор
.
Это означает, что этот набор![]() ,
гдеi=1,…,m.
Далее поступаем следующим образом:
,
гдеi=1,…,m.
Далее поступаем следующим образом:
1 шаг:
применяем к набору
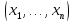 алгоритм
алгоритм![]() ,
вычисляющий функцию
,
вычисляющий функцию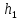 .
Так как функция
.
Так как функция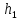 по условию алгоритмически вычислимая
функция, то за конечное число шагов
алгоритм
по условию алгоритмически вычислимая
функция, то за конечное число шагов
алгоритм![]() дает конечный результат для функции
дает конечный результат для функции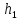 .
.
2 шаг:
применяем к набору
 алгоритм
алгоритм![]() ,
вычисляющий функцию
,
вычисляющий функцию .
Так как функция
.
Так как функция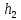 по условию алгоритмически вычислимая
функция, то через конечное число шагов
работа алгоритма
по условию алгоритмически вычислимая
функция, то через конечное число шагов
работа алгоритма![]() завершается результативно, т.е. будут
вычислено значение функция
завершается результативно, т.е. будут
вычислено значение функция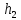 на наборе
на наборе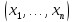 и т.д. Если работа всех алгоритмов
и т.д. Если работа всех алгоритмов![]() на наборе
на наборе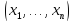 завершилась результативно, т.е. вычислены
соответствующие значения
завершилась результативно, т.е. вычислены
соответствующие значения ,
на следующий шаг, т.е.
,
на следующий шаг, т.е.
m+1–шаг:
применяем
алгоритм
![]() ,
вычисляющий функциюg,
к набору
,
вычисляющий функциюg,
к набору
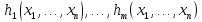 .
В силу свойства алгоритмически
вычислимости функциюg,
через конечное число шагов алгоритм
.
В силу свойства алгоритмически
вычислимости функциюg,
через конечное число шагов алгоритм
![]() завершает работу на наборе
завершает работу на наборе результативно, и этот результат будем
считать значением функцииf,
так как по определению операции
подстановки
результативно, и этот результат будем
считать значением функцииf,
так как по определению операции
подстановки
f
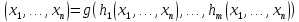 .
.
В случае, когда
алгоритм
![]() гдеi=1,…,m
не останавливается или завершает работу
нерезультативно, будем считать, что
искомый алгоритм для вычисления данной
функции, т.е. функции f
гдеi=1,…,m
не останавливается или завершает работу
нерезультативно, будем считать, что
искомый алгоритм для вычисления данной
функции, т.е. функции f
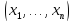 ,
не существует.
,
не существует.
Основные свойства операции примитивной рекурсии
10. Сохранение свойства всюду определенности функций,
т.е если
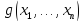 и
и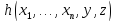 всюду определенные функции, то
всюду определенные функции, то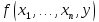 тоже будет всюду определенная функция,
тоже будет всюду определенная функция,
где f=R(g,h).
Доказательство.
Берем произвольный набор
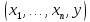 и докажем, что на этом наборе функцияf
определена. Доказательство проводим
методом математической индукции по y.
и докажем, что на этом наборе функцияf
определена. Доказательство проводим
методом математической индукции по y.
1 шаг.
Пусть y=0.
Тогда по определению операции ПР
получаем, что

Так как функция g
всюду определенная функция по условию,
то функция f
определена
на наборе
 .
.
2 шаг.
Предположим, что функция f
определена на наборе
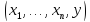
3 шаг.
Доказываем что функции f
определена на наборе
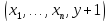 .
.
По определению операции ПР получаем, что
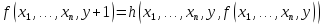 .
.
А функция h
обладает свойством всюду определенности
по условию. Следовательно, функция f
определена на наборе
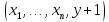 .
Так как функцияf
является
арифметической функцией, то метод
математической индукции позволяет
сделать вывод, что она всюду определена.
.
Так как функцияf
является
арифметической функцией, то метод
математической индукции позволяет
сделать вывод, что она всюду определена.
20. Сохранение алгоритмической вычислимости функций, т.е.,
если
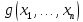 и
и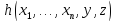 являются алгоритмически вычислимыми
функциями, то
алгоритм
являются алгоритмически вычислимыми
функциями, то
алгоритм
![]() ,
вычисляющий функцию
,
вычисляющий функцию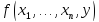 ,
гдe
,
гдe
: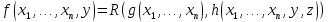 .
.
