1.2. Характеристики центра группирования значений случайных величин

Математическим ожиданием  М(X) дискретной случайной величины Х  называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е.

Мода Mo(X) дискретной случайной величины Х - это значение случайной величины, имеющее наибольшую вероятность. На многоугольнике распределения мода - это абсцисса самой высокой точки. Бывает, что распределение имеет не одну моду. Медиана Me (X) — значение х_i, при котором площадь под кривой распределения делится пополам. В общем случае значения М(Х), Мо(Х), Me (X) могут не совпадать.

1.3. Характеристики степени рассеяния значения случайной величины

Дисперсия D (X) случайной величины X— это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Среднее квадратическое отклонение s(x) — это корень квадратный из дисперсии (является моментом второго порядка).

Коэффициент вариации используют для сравнения рассеивания двух и более признаков, имеющих различные единицы измерения. Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах. Он вычисляется по формуле:

,

где - искомый показатель,- среднее квадратичное отклонение,M(X) – математическое ожидание.

1.4. Основные законы распределения

Равномерный закон распределения. Непрерывная случайная величину Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности f(x) случайной величины X постоянна, т.е. f(x) имеет вид:

Рисунок 1. Равномерный закон распределения

Математическое ожидание равномерного распределения: M(X) = (a + b)/2 Дисперсия равномерного распределения: D(X) = (b - a)²/12 Среднее квадратичное отклонение равномерного распределения: σ(X) = (b - a)/(2√3)

Нормальный закон распределения (закон Гаусса). Непрерывная случайная величина Х имеет нормальный закон распределения с параметрами a и σ, если ее плотность вероятности имеет вид:

Известно, что 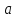=M(X) и . График нормального распределения имеет куполообразную форму, он симметричен относительно своего математического ожидания, а на степень его островершинности влияет величина среднего квадратичного отклонения.

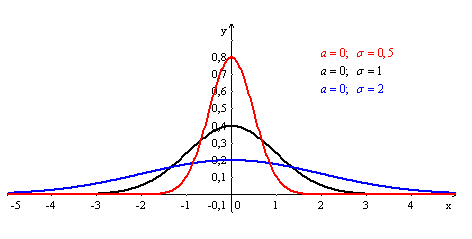
Рисунок 2. График плотности случайной величины, в случае нормального распределения.

Мода и медиана нормального распределения равны: Mo(X) = ; Me(X) =, где- математическое ожидание. Интегральная функция нормального распределения вероятностей:

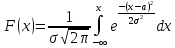
Интегральная функция распределения вероятностей показывает вероятность того, что случайная величина X примет значение меньшее, чем x: F(x) = P(X < x). Численно она равна площади криволинейной трапеции, ограниченной сверху графиком плотности вероятности, снизу осью абсцисс случайной величины, на интервале от -∞ до x. Ниже дана иллюстрация.

Рисунок 3. Интегральная функция нормального распределения.

Показательный (экспоненциальный) закон распределения. Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром λ >0, если ее плотность вероятности имеет вид:

где λ — постоянная положительная величина.

Математическое ожидание: .

Дисперсия: .

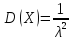Используя свойство два плотности распределения (Несобственный интеграл от плотности распределения в пределах от - доравен единице) можно найти функцию распределения экспоненциального закона:

Рисунок 4. Экспоненциальный закон распределения.

Распределение хи-квадрат. Пусть независимые случайные величины X_i (i = 1, 2, ..., n) — распределены по стандартному нормальному закону. Тогда говорят, что сумма квадратов этих величин

распределена по закону χ² («хи квадрат») с n степенями свободы

Плотность распределения случайной величины χ² имеет следующий вид:

Здесь — гамма-функция.

Отсюда видно, что распределение «хи квадрат» определяется одним параметром n —независимым числом степеней свободы.

С увеличением числа степеней свободы распределение медленно приближается к нормальному.

Рисунок 5. Распределение хи-квадрат.

Основные характеристики распределение хи квадрат (математическое ожидание и дисперсия):

Распределение Стьюдента. Случайная величина есть отношение двух независимых случайных величини, то есть

Распределение случайной величины называется распределением Стьюдента сстепенями свободы. Его плотность задаётся формулой

Математическое ожидание и дисперсия случайной величины, подчинённой распределению Стьюдента , есть

Как и в случае и хи-квадрат распределением, при увеличении распределение Стьюдента стремиться к нормальному, более того, стандартизованному нормальному (то есть с нулевым математическим ожиданием и единичной дисперсией). Распределение Стьюдента, как хи-квадрат распределение, широко применяется в задачах математической обработки измерений.

Распределение Фишера. Пусть случайная величина равна отношению двух независимых случайных величини, то есть

Распределение случайной величины называется распределением Фишера систепенями свободы. Оно имеет следующую плотность вероятности

Математическое ожидание случайной величины, подчинённой распределению Фишера, определяется по формуле

Между случайными величинами, имеющими нормальное распределение: хи-квадрат, Стьюдента и Фишера, имеют место соотношения