Заработная плата работников

Показатели	Средняя заработная плата, руб.	Число обследованных работников, чел.	Среднее квадратическое отклонение, руб.	Удельный вес женщин в общей численности работников, %
Работники государственных предприятий и учреждений частных предприятий	3900 5600	400 600	800 1200	40 50

С вероятностью 0,954 определите пределы, в которых будет находиться средняя заработная плата работников, и долю женщин в общей численности работников.

Решение

1. Определим среднюю заработную плату работников:

= = = 4920 руб.

2. Вычислим среднюю из групповых дисперсий:

=

3. Определим предельную ошибку выборки по формуле

= 2 = 63,50 руб.

4. Средняя заработная плата работников находиться в пределах:

4520– 63,50

4856,50 4983,50 руб.

Таким образом, с вероятностью 0,954можно гарантировать, что средняя заработная плата работников в генеральной совокупности будут не менее 4856 руб. 50 коп., но не более 4856 руб. 50 коп.

5. Долю женщин в общей численности работников определим по формуле

= = .

6. Выборочную дисперсию альтернативного признака вычислим по формуле

=

Ошибку для доли определим по формуле:

_w = 2 = 0,030, или 3,0%.

7. Доля женщин в общей численности работников находится в пределах:

w – _w w + _w , т.е. 46,0 – 3,0%46,0 + 3,0%.

Следовательно, с вероятностью 0,954 можно утверждать, что доля женщин в генеральной совокупности находится в пределах от 43 до 49%.

Серийная выборка осуществляется, как правило, бесповоротным способом. Предельные ошибки выборочной средней определяются по формуле

, где

- межсерийная дисперсия;

r – число отработанных серий;

R – число серий в генеральной совокупности.

Задание 4

В одном из учебных заведений насчитывается 50 студенческих групп. С целью изучения успеваемости студентов произведена 10%-ная серийная выборка, в которую попали 5 групп студентов. В результате обследования установлено, что средняя успеваемость в группах составила: 3.2; 3,4; 3,8; 4,0; 4,1 балла. С вероятностью 0,997 определите пределы, в которых будет находиться средний балл студентов учебного заведения.

Решение.

Средний балл всех студентов находиться в пределах:

- + .

Определим выборочную среднюю серийной выборки:

=

Дисперсию средней выборки определим по формуле

, где

- выборочная средняя каждой серии;

- выборочная средняя серийной выборки.

Значение дисперсии составляет

= = 0,12.

Рассчитаем предельную ошибку выборки для средней по формуле

= 0,4 балла.

С вероятностью 0,997 можно утверждать, что средний балл всех студентов учебного заведения находится в пределах = 3,70,4, или 3,34,1 балла.

Задание 5

Предприятие выпустило 100 партий готовой продукции А по 50 шт. в каждой из них. Для проверки качества готовой продукции была проведена 10%ная серийная выборка, в результате которой установлено, что доля бракованной продукции составила 12%. Дисперсия серийной выборки равна 0,0036.

С вероятностью 0,997 определите пределы, в которых находится доля бракованной продукции А.

Решение

Доля бракованной продукции А будет находиться в пределах

w– _ww+ _w .

Определим предельную ошибку выборки по формуле:

= 0,054, или 5,4%.

С вероятностью 0,997 можно утверждать, что доля банковской продукции А находится в пределах 6,6%17,4%.

Для типичной выборки

.

Для серийной выборки

.

Задание 6

Определите численность рабочих, которую необходимо отобрать в выборочную совокупность с тем, чтобы при изучении их средней заработной платы предельная ошибка выборки не превышала 30 руб. с вероятностью 0,997, если по данным предыдущего обследования среднее квадратическое отклонение составило 70 руб.

Решение

Поскольку способ отбора не указан, расчет следует проводить по формуле повторного отбора

= =

Задание 7

В городе Н проживает 100 тыс. чел. С помощью механической выборки определите долю населения со среднедушевым денежными доходами до 1500 руб. в месяц. Какова должна быть численность выборки, чтобы с вероятностью 0,997 ошибка выборки не превышала 2%, если на основе предыдущих обследований известно, что дисперсия равна 0,24?

Решение

Определим необходимую численность выборки по формуле:

=

Задание 8

• Укажите, что произойдет с предельной ошибкой выборки, если дисперсию (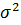) уменьшить в 4 раза, численность выборки увеличить в 9 раз, а вероятность исчисления изменится с 0,683 до 0,997 (t=1 и t = 3):

а) уменьшится в 18 раз;

б) увеличится в 18 раз;

в) уменьшится в 2 раза;

г) не изменится.

Решение

=t = 3t = t = t = .

Задание 9

• В выборах мэра примут участие около 1 млн избирателей: кандидат Р. будет выбран, если за него проголосуют более 50% избирателей. Накануне выборов проведен опрос случайно отобранных 1000 избирателей: 540 из них сказали, что будут голосовать за Р. Укажите, можно ли при уровне доверительной вероятности 0,954 утверждать, что Р. победит на выборах:

а) можно;

б) нельзя.

Решение:

Доля избирателей, которые будут голосовать за кандидата Р., будет находится в пределах

w– _ww+ _w .

Выборочная доля составляет:

_w = t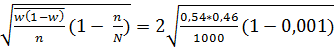 = 0,032, или 3,2%.

, что доля избирателей, проголосовавших за кандидата Р., будет находится в пределах

54 – 3,2 54 + 3,2;

50,2% 57,2%.

Задание 10

• Исследуемая партия состоит из 5 тыс. деталей. Предполагается, что партия изделий содержит 8% бракованных. Определите необходимый объем выборки, чтобы с вероятностью 0,997 установить долю брака с погрешностью не более 2%:

а) 1650;

б) 1244;

в) 1300.

Решение

Определим необходимую численность выборки по формуле

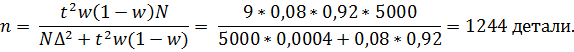
Задание 11

• Из партии готовой продукции методом случайного бесповторного отбора отобрано 250 изделий, из которых 5 оказались бракованными. Определите с вероятностью 0,954 возможные пределы процента брака во всей партии. Объем выборки составляет 10% всего объема готовой продукции:

а) 2%1,6%;

б) 10%2%;

Решение

Процент брака во всей партии будет находится в пределах

w– _ww+ _w .

выборочная доля составляет:

= .

t = 0,0168, или 1,68%.

С вероятностью 0,954 можно утверждать, что процент банка во всей партии будет находиться в пределах р = 2%1,68%, или0,32% 3,68% .

Задание 12

В студенческой группе из 25 человек трое имеют задолженности по результатам зимней сессии. Каковы средняя успеваемость группы и дисперсия успеваемости?

Решение

Доля успевающих студентов равна:

Р=

Или 88% и есть средняя успеваемости.

=рq=0,88*0,12=0,1056.

Задание 13

Имеются следующие данные о продажах картофеля на рынках:

Номер рынка	Цена на картофель, руб./кг	Выручка от продажи (товарооборот), тыс. руб.
1 2 3	4 5 6	160 100 60

Определите среднюю по трем рынкам вместе цену на картофель. Найденная вами величина будет находиться в интервале:

а) до 4,6;

б) 4,6 – 5,0;

в) 5,0 и более.

Решение

Очевидно, что объем продаж картофеля на рынках разный. Следовательно, форма расчетов – средняя взвешенная. Нетрудно видеть, что весами при вычислениях являются выручки от продаж М, которые представляют собой произведение цен х на количество проданного картофеля f, т.е. М = xf. Одно это требует использования в расчетах средней гармонической взвешенной:

Здесь суммарная выручка от продажи картофеля на всех рынках составила 320 тыс. руб., а общий объем продаж – 70 т.