Эллипс

Творческая работа

Линии второго порядка

«Эллипс»

Выполнил: Егурнов Евгений

12 группа

Каноническое уравнение

Эллипс – это множество всех точек плоскости, сумма расстояний до каждой из которых от двух данных точек , называемых фокусами эллипса, – есть величина постоянная, численно равная длине большой оси этого эллипса: . 

Каноническое уравнение эллипса имеет вид  , где   – положительные действительные числа, причём . 

Пр. Эллипс задан уравнением 

Сначала приведём уравнение к каноническому виду:

Это позволит моментально определить вершины эллипса, которые находятся в точках . В данном случае : Отрезок  называют большой осью эллипса; отрезок  – малой осью; число  называют большой полуосью эллипса;  число  – малой полуосью.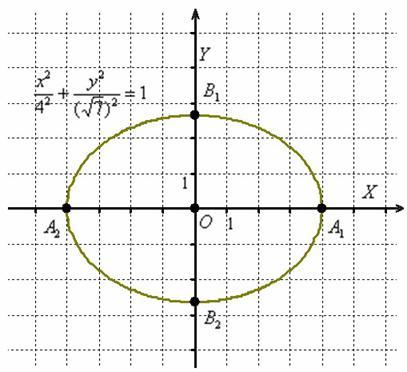

.

Любой эллипс симметричен относительно координатных осей, а также относительно начала координат.

Основное соотношение и частный случай

Эксцентриситетом эллипса называют отношение , которое может принимать значения в пределах .

Чем ближе значение эксцентриситета эллипса к единице, тем эллипс более продолговат.

Чем ближе значение эксцентриситета к нулю, тем эллипс больше похож на окружность.

Окружность – это частный случай эллипса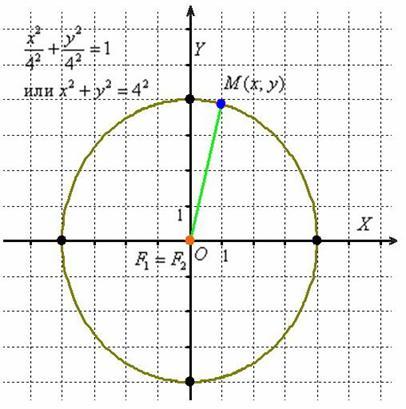

Действительно, в случае равенства полуосей каноническое уравнение эллипса принимает вид , который рефлекторно преобразуется к  – хорошо известному из школы уравнению окружности с центром в начале координат радиуса «а».

На практике чаще используют запись: . Радиусом называют длину отрезка , при этом каждая точка  окружности удалена от центра  на расстояние радиуса.

Заметьте, что определение эллипса остаётся полностью корректным: фокусы совпали , и сумма длин совпавших отрезков  для каждой точки окружности – есть величина постоянная. Так как расстояние между фокусами , то эксцентриситет  любой окружности равен нулю.

Директориальное свойство

Директрисами эллипса называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее. При , когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).

Эллипс с эксцентриситетом  можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки  (фокуса) к расстоянию до заданной прямой  (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету  (директориальное свойство эллипса). Здесь  и  — один из фокусов эллипса и одна из его директрис, расположенные по одну сторону от оси ординат канонической системы координат, т.е.  или .

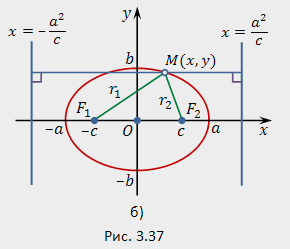
В самом деле, например, для фокуса  и директрисы  (рис.3.37,6) условие  можно записать в координатной форме:

Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению эллипса. Аналогичные рассуждения можно провести для фокуса  и директрисы .

Оптическое свойство

Касательная эллипса образует в точке касания равные острые углы с фокальными радиусами.

x2 a2

+

y2 b2

=1.

Доказательство. Уравнение эллипса 

Для получения уравнения касательной продифференцируем 

2x a2

+

2yy b2

=0.

Вектор, лежащий на касательной, 

 

= {a2y, b2x, 0}

 O1A

= {c+x,y,0}

 AO2

= {cx,y,0}

cos =			(     ,  O1A   ) a+x	,
cos =	(     ,  AO2   ) ax	. где  = c/a - эксцентриситет.

Докажем

cos = cos

a2y(c+x)b2xy a+x

=

a2y(cx)+b2xy ax

Получим

a3xyab2xya2xyc=0

a2b2c2=0

Преобразуем и получим

Сократим на axy, подставим  = c/a, получим тождество 

Литература

1. http://www.mathprofi.ru/linii_vtorogo_poryadka_ellips_i_okruzhnost.html

2. http://mathhelpplanet.com/static.php?p=ellips

3. http://vuz.exponenta.ru/PDF/optsvel.html