
- •Введение
- •Кинематика
- •5. Кинематика вращательного движения.
- •Динамика материальной точки
- •6. Первый закон Ньютона.
- •8. Механические системы.
- •9. Масса.
- •10.Импульс.
- •11.Второй закон Ньютона
- •12.Принцип независимости действия сил.
- •13.Третий закон Ньютона
- •14.Закон сохранения импульса
- •15.Закон движения центра масс.
- •16. Силы в механике.
- •1) Силы тяготения (гравитационные силы).
- •17. Работа, энергия, мощность.
- •18. Кинетическая и потенциальная энергия механической системы
- •19.Закон сохранения энергии.
- •20. Соударения
- •Механика твердого тела
- •21. Момент инерции.
- •22.Кинетическая энергия вращения.
- •23. Момент силы.
- •24.Основное уравнение динамики вращательного движения твердого
- •25. Момент импульса и закон его сохранения.
- •26.Сопоставим основные величины и соотношения для поступательного движения тела и для его вращения вокруг неподвижной оси.
- •Деформации твердого тела
- •27. Деформации твердого тела
- •28. Закон Гука.
- •Элементы механики жидкостей
- •29. Давление в жидкости и газе.
- •30.Уравнение неразрывности.
- •31 .Уравнение Бернулли.
- •32. Вязкость (внутреннее трение)
- •33.Два режима течения жидкостей.
- •34.Методы определения вязкости
- •Потенциальное поле сил.
- •35.Поле сил тяготения.
- •36. Космические скорости.
- •Элементы специальной теории относительности
- •37. Преобразования Галилея
- •38.Постулаты Эйнштейна.
- •39.Преобразования Лоренца.
- •40. Основные соотношения релятивистской динамики.
- •Свободные колебания
- •1. Колебания. Общий подход к изучению колебаний различной физичес кой природы.
- •2. Гармонические колебания и их характеристики.
- •3. Дифференциальное уравнение гармонических колебаний.
- •4. Метод векторных диаграмм.
- •5. Экспоненциальная форма записи гармонических колебаний.
- •6. Механические гармонические колебания.
- •7. Энергия материальной точки, совершающей гармонические колебания.
- •8. Гармонический осциллятор.
- •9. Пружинный маятник.
- •10. Математический маятник.
- •11 .Физический маятник.
- •12.Сложение гармонических колебаний.
- •13. Биения.
- •14. Разложение Фурье.
- •15. Сложение взаимно перпендикулярных гармонических колебаний одинаковой частоты.
- •16.Линейно поляризованные колебания.
- •17. Циркулярно поляризованные колебания.
- •18 .Фигуры Лиссажу.
- •Затухающие и вынужденные колебания
- •19. Затухающие колебания.
- •20.Дифференциальное уравнение свободных затухающих колебаний линейной системы
- •21. Декремент затухания.
- •22.Добротность колебательной системы.
- •Волны в упругой среде.
- •23.Волновой процесс.
- •24.Упругие волны.
- •36. Упругая гармоническая волна.
- •37.Бегущие волны.
- •25.Уравнение плоской волны.
- •25.Фазовая скорость.
- •26. Уравнение сферической волны.
- •28.Принцип суперпозиции.
- •29.Групповая скорость.
- •30. Интерференция волн.
- •31. Стоячие волны.
- •32. Эффект Доплера.
- •2)Приемник приближается к источнику, а источник покоится:
- •3)Источник приближается к приемнику, а приемник покоится:
- •4)Источник и приемник движутся друг относительно друга.
- •1. Статистический и термодинамический методы исследования.
- •2. Термодинамическая система.
- •3. Температура.
- •4. Идеальный газ.
- •5.Закон Бойля-Мариотта.
- •6. Закон Авогадро,
- •7. Закон Дальтона.
- •8 .Закон Гей-Люссака.
- •9. Уравнение состояния идеального газа.
- •10.Основное уравнение молекулярно-кинетической теории идеальных газов.
- •11 .Средняя квадратичная скорость молекул идеального газа:
- •18.Средняя длина свободного пробега молекул.
- •19.Эксперименты, подтверждающие молекулярно-кинетическую теорию.
- •20.Явления переноса.
- •21 .Теплопроводность.
- •22. Диффузия.
- •23.Внутреннее трение (вязкость).
- •24.Внутренняя энергия термодинамической системы.
- •25. Число степеней свободы.
- •26.3Акон Больцмана о равномерном распределении энергии по степеням свободы (закон равнораспределения).
- •27. Первое начало термодинамики.
- •28.Работа газа при его расширении.
- •29. Теплоемкость.
- •30.Молярная теплоемкость при постоянном объеме.
- •31 .Молярная теплоемкость при постоянном давлении. Уравнение Майера.
- •36. Работа газа в адиабатическом процессе.
- •39. Кпд кругового процесса.
- •40. Обратимый и необратимый процессы.
- •41 .Энтропия.
- •42. Изменение энтропии.
- •Изменение энтропии в процессах идеального газа
- •43. Статистическое толкование энтропии.
- •44. Принцип возрастания энтропии.
- •45. Второе начало термодинамики.
- •46.Третье начало термодинамики.
- •47.Тепловые двигатели и холодильные машины.
- •48. Теорема Карно
- •50.Уравнение Ван-дер-Ваальса.
- •51. Изотермы реальных газов.
- •52. Внутренняя энергия реального газа.
- •53.Жидкости и их описание.
- •54. Поверхностное натяжение.
- •55. Смачивание.
- •56. Давление под искривленной поверхностью жидкости.
- •57. Капиллярные явления.
- •58. Кристаллические и аморфные твердые тела.
- •59. Типы кристаллов.
- •60.Дефекты в кристаллах.
- •61 .Теплоемкость твердых тел.
- •62. Изменение агрегатного состояния.
- •63.Фазовые переходы.
- •64.Диаграмма состояния.
- •65.Уравнение Клапейрона-Клаузиуса
- •66.Анализ диаграммы состояния.
- •Приложение
- •6.Вектор.
- •12.Градиент.
- •13.Поток поля через поверхность.
- •14.Производная по объему.
- •15. Дивергенция векторного поля.
- •17.Оператор Лапласа.
- •18.Ротор векторного поля.
- •19.Теорема Стокса.
- •Греческий алфавит
- •Приставки к обозначению единиц
- •Основные физические постоянные
36. Работа газа в адиабатическом процессе.
В
адиабатическом
процессе
δA
= -dU
, поэтому
δА
=-![]() CvdT.
Если
газ
CvdT.
Если
газ
адиабатически расширяется от объема V1 до V2, то его температура уменьшается от T1 до Т2 и работа расширения идеального газа
 Откуда
получаем
Откуда
получаем
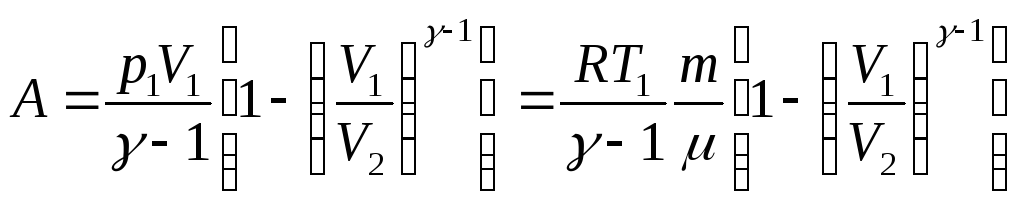 ,
используя
уравнение
Менделеева-Клапейрона
pV
=
,
используя
уравнение
Менделеева-Клапейрона
pV
=
![]() RT.
RT.
Работа адиабатического расширения 1-2 (заштрихованная площадь) меньше, чем при изотермическом процессе. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.
37. Политропические процессы (С = const).
Процесс, в котором теплоемкость остается постоянной (С = const) называется политропическим.
Рассмотренные выше изохорный, изотермический, изобарный и адиабатический процессы — это частные случаи политропного процесса.
Уравнение политропы
pVn = const
где
коэффициент
![]() называется
показателем
политропы.
называется
показателем
политропы.
Значения теплоемкости и показателя политропы для разных процессов приведены в таблице.
|
Процесс |
С |
n |
|
Адиабатический |
С = 0 |
n = у |
|
Изотермический |
С = ∞ |
n = 1 |
|
Изобарический |
C=Cp |
n = 0 |
|
Изохорный |
C=CV |
n =±∞ |
Теплоемкость при изотермическом процессе бесконечно велика, поскольку dT = 0, в то время как δQ≠0.
Теплоемкость при адиабатическом процессе равна нулю, поскольку δQ=0, в то время как dT ≠ 0
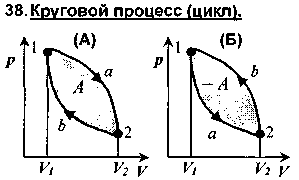
Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное состояние. На (р,V)-диаграмме цикл изображается замкнутой кривой, где участок 1-2 соответствует расширению, а 2-1 — сжатию газа.
Работа расширения А1 (площадь фигуры 1a2V2V11) положительна: А1 >0. Работа сжатия А2 (площадь фигуры 2b1V1V22) отрицательна: А2 < 0.
Работа за цикл А определяется площадью, охватываемой замкнутой кривой:
А = А1 + А2
Таким образом, работа — это функция не только состояния термодинамической системы, но и вида процесса, который происходит. Поэтому работа не является однозначной функцией состояния (такой, как внутренняя энергия). Из первого начала термодинамики следует, что теплота Q, так же как и работа А, является функцией процесса, который происходит с системой.
Цикл
называется
прямым,
если
за
цикл
совершается
положительная
работа A
=
![]() pdV
> О
(цикл
протекает
по
часовой
стрелке
—
рисунок
(А)).
pdV
> О
(цикл
протекает
по
часовой
стрелке
—
рисунок
(А)).
Цикл называется обратным, если за цикл совершается отрицательная
работа
А
=![]() pdV
< О
(цикл
протекает
против
часовой
стрелки
—
рисунок
(Б)).
pdV
< О
(цикл
протекает
против
часовой
стрелки
—
рисунок
(Б)).
Прямой цикл используется в тепловых двигателях (совершают работу за счет полученной извне теплоты). Обратный цикл используется в холодильных машинах (за счет работы внешних сил теплота переносится к телу с более высокой температурой).
39. Кпд кругового процесса.
В результате кругового процесса система возвращается в исходное состояние, следовательно, полное изменение внутренней энергии равно нулю. Поэтому Q = ΔU + А = А, т.е. работа, совершаемая за цикл, равна количеству полученной извне теплоты. Если в ходе кругового процесса система не только получает количество теплоты Q1, но и теряет (отдает) количество теплоты Q2, то Q= Q1- Q2 .
Термический коэффициент полезного действия для кругового процесса — это величина, равная отношению работы, совершенной системой, к количеству теплоты, полученному в этом цикле системой:
![]()
