
- •Министерство сельского хозяйства р.Ф.
- •Инструкция по технике безопасности, для работающих в лабораториях физики. Общие положения
- •Основные положения.
- •Надзор.
- •Меры оказания первой помощи при несчастных случаях
- •Инструкция по подготовке к лабораторному занятию, проведению и отчёту по работе.
- •Введение в теорию измерений физических величин
- •Задача измерений. Основные понятия и их определения
- •Пример нахождения объема цилиндра
- •Графическая обработка результатов измерения
- •Лабораторная работа №1 определение породы древесины по плотности.
- •Теоретическое введение
- •Описание штангенциркуля и микрометра.
- •Порядок выполнения работы:
- •Контрольные вопросы:
- •Статическое трение
- •Кинематическое трение Трение скольжения.
- •Трение качения и верчения.
- •Значение коэффициентов трения скольжения и трения качения для некторых материалов
- •Описание установки
- •Порядок выполнения работы
- •Определение статического коэффициента трения скольжения
- •Определение коэффициента трения качения
- •Определение коэффициента трения скольжения
- •Дополнительное задание
- •Контрольные вопросы:
- •Лабораторная работа №3
- •Описание установки
- •Порядок выполнения работы
- •Дополнительное задание
- •Контрольные вопросы
- •Лабораторная работа №4
- •Описание установки и методики эксперимента
- •Порядок выполнения работы
- •Определение момента инерции маховика и силы трения в опоре
- •Дополнительное задание
- •Контрольные вопросы
- •Лабораторная работа №5 термогравиметрический способ измерения влажности семян
- •Теоретическое введение
- •Описание установки
- •Порядок выполнения работы:
- •Контрольные вопросы:
- •Лабораторная работа №6 определение моментов инерции тел методом крутильных колебаний
- •Введение
- •Описание установки и метода измерения
- •Порядок выполнения работы
- •Определение коэффициента упругости проволоки и момента
- •Описание установки
- •Определение коэффициента вязкости жидкостей по методу Стокса
- •Дополнительное задание
- •Описание установки и методика выполнения работы
- •Порядок выполнения работы
- •Дополнительное задание
- •Приложение к лабораторной работе №8
- •Описание эксперимента
- •Лабораторная работа №9 определение постоянной больцмана по измерению парциального давления эфира
- •Введение
- •Описание метода измерения и установки
- •Порядок выполнения работы
- •Определение постояной больцмана
- •Дополнительное задание
- •Описание установки
- •Порядок выполнения работы
- •Определение универсальной газовой постоянной
- •Дополнительное задание
- •Контрольные вопросы
- •Лабораторная работа №11
- •Введение
- •Описание установки
- •Порядок выполнения работы
- •Определение коэффициента линейного расширения
- •Дополнительное задание
- •I. Определение коэффициента поверхностного натяжения методом отрыва кольца
- •Порядок выполнения работы
- •Определение коэффициента поверхностного натяжения методом отрыва кольца
- •II. Определение коэффициента поверхностного натяжения методом отрыва колец
- •Порядок выполнения работы
- •Лабораторная работа №13 изучение гармонических колебаний
- •Введение
- •Определение ускорения силы тяжести
- •Дополнительное задание
- •Описание установки и метода измерений
- •Зависимость периода колебаний физического маятника от положения груза а2
- •Определение ускорения силы тяжести с помощью оборотного маятника
- •Указания по оценке погрешности
- •Порядок выполнения работы
- •Дополнительное задание
- •II. Описание установки и методика измерений
- •Описание установки
- •Определение собственной частоты колебаний пружинного маятника
- •3. Определение логарифмического декремента затухания методом сравнения амплитуд
- •4. Исследование зависимости затухания колебаний от сопротивления среды.
- •III. Выполнение работы задание 1. Определить собственную частоту колебаний пружинного маятника
- •Задание 2. Определить логарифмический декремент затухания
- •Задание 3. Исследование зависимости затухающих колебаний от сопротивления среды.
- •Контрольные вопросы
- •Литература
- •Оглавление
Введение
Гармоническим называют такое колебательное движение, при котором на тело массы m действует возвращающая сила F, пропорциональная отклонению x от положения равновесия.
На рисунке 13.1. показан пружинный маятник, расположенный горизонтально. Это шарик массой m, прикрепленный к пружине обладающей упругостью k.
Если шарик вывести из положения равновесия (растянуть или сжать пружину), то вследствии ее деформации возникает сила упругости, возвращающая шарик в положение равновесия
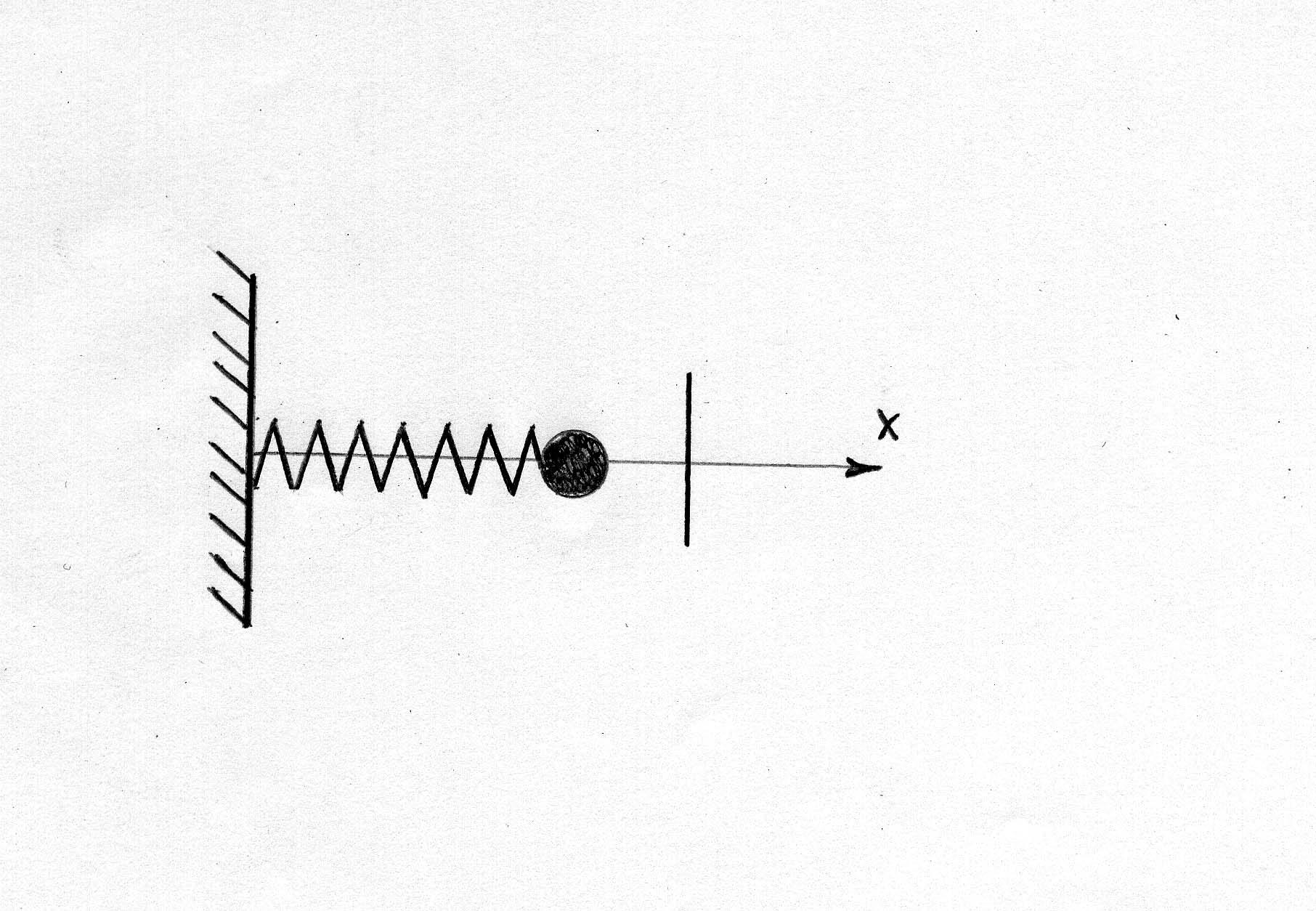
Рис. 13.1.
![]() (13.1.)
(13.1.)
где k – коэффициент возвращающей силы. Знак минус означает противоположность направлений х и F. Эта сила сообщает телу ускорение а и может быть выражена по закону Ньютона:
![]() (13.2.)
(13.2.)
![]() - ускорение. Из
формул (13.1.) и (13.2.) получаем дифференциальное
уравнение гармонических колебаний
- ускорение. Из
формул (13.1.) и (13.2.) получаем дифференциальное
уравнение гармонических колебаний
![]() (13.3.)
(13.3.)
Решением этого уравнения является уравнение вида:
![]() (13.4.)
(13.4.)
Здесь А – амплитуда колебаний,
- начальная фаза,
(t+) – фаза колебаний в момент времени t,
- циклическая частота.
Согласно решению уравнению (13.3.)
![]()
![]() (13.5.)
(13.5.)
Так как циклическая частота зависит только от свойств колеблющейся системы (массы и упругости), то ее называют собственной циклической частотой системы.
Примерно по гармоническому закону происходит движение математического маятника (рис.13.2.), первоначально выведенного из положения равновесия на малый угол 50.
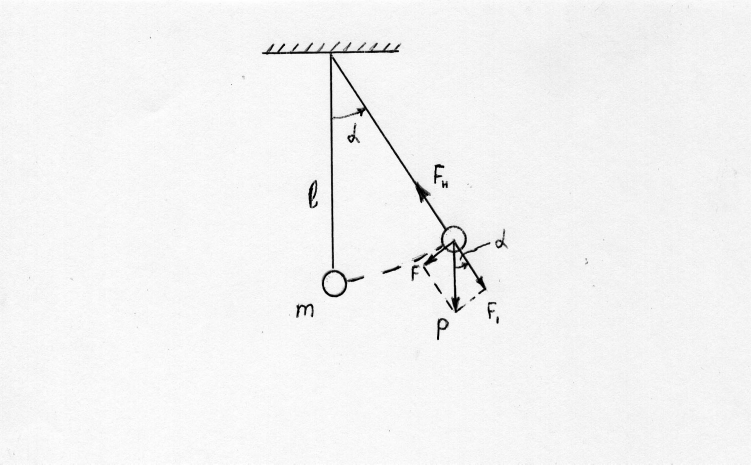
Рис.13.2.
Напомним, что математическим маятником называется материальная точка, подвешенная на нерастяжимой нити. Действующая на материальную точку массой m сила тяжести Р=mg раскладывается на две взаимно перпендикулярные составляющие, одна из которых F1 растягивает нить, а вторая –F вызывает ускорение в сторону положения равновесия, ее называют возвращающей силой. Она равна
![]()
Относительно точки подвеса тело совершает вращательное движение; поэтому для вывода уравнения движения надо воспользоваться законом динамики для вращательного движения.
Возвращающая сила создает возвращающий момент силы
![]()
Так как угол мал, то sin (здесь выражен в радианах). Поэтому
![]() (13.7.)
(13.7.)
Знак (-) указывает, что сила тяжести препятствует отклонению тела на угол . Этот момент силы вызовет движение шарика с угловым ускорением равным второй производной угла по времени, т.е.
![]() (13.8.)
(13.8.)
где I – момент инерции шарика относительно точки подвеса.
![]() (13.9.)
(13.9.)
Подставив уравнение (13.9.) в уравнение (13.8.) и приравняв правые части полученного уравнения и уравнения (13.7.) получим уравнение движения математического маятника
![]() (13.10.)
(13.10.)
Если сравним его с уравнением (13.3.), то собственная циклическая частота математического маятника будет зависеть от длины и ускорения силы тяжести, т.е.
![]() (13.11.)
(13.11.)
Это значит, что роль массы в этом случае выполняет длина нити, а упругость системы – ускорение силы тяжести.
Известно, что период колебаний связан с частотой соотношением:
![]() (13.12.)
(13.12.)
Подставив в уравнение (13.12.) значение для пружинного маятника или для математического (уравнение (13.11.), получим для математического маятника
![]() (13.13.)
(13.13.)
Это уравнение используют для измерения ускорения силы тяжести с помощью математического маятника.
Из уравнения (13.13.) легко определить ускорение свободного падения:
![]() (13.14.)
(13.14.)
Непосредственное измерение длины маятника l не представляется возможным, т.к. центр тяжести лабораторного маятника не совпадает точно с геометрическим центром шарика. Поэтому при определении ускорения силы тяжести наблюдают колебания маятника для различных l и определяют периоды колебаний Т1 и Т2. Тогда g легко выразить через Т1 и Т2 и разность длин маятников. Окончательно имеем:
![]() (13.15.)
(13.15.)
ОПРЕДЕЛИТЬ УСКОРЕНИЕ СИЛЫ ТЯЖЕСТИ
Упражнение 1.
Установите шарик маятника на высоте h1 от пола. Измерьте эту высоту.
Отведите шарик от положения равновесия на 4-6 см, отпустите его и измерьте время t 50 полных колебаний при помощи секундомера.
Период определяют по уравнению
![]() (13.16.)
(13.16.)
Поднимите шарик маятника на высоту h2 от пола. Повторите измерения пункта 2 и вычислите период колебаний для этой длины по уравнению (13.16.)
По уравнению (13.15.), подставив вместо
 подсчитайте ускорение силы тяжестиg.
подсчитайте ускорение силы тяжестиg.Рассчитайте абсолютную и относительную ошибки измерений. Абсолютную погрешность рассчитываем по правилам вычисления абсолютной погрешности косвенных измерений.
Из
уравнения (13.15.) следует, что ускорение
свободного падения есть функция найденных
периодов Т1,
Т2
двух математических маятников с разными
длинами l1
и l2,
а также функция разности длин этих
маятников. Обозначим
![]() ,
тогда максимальная возможная погрешность
равна
,
тогда максимальная возможная погрешность
равна
![]() .
.
Взяв частные производные уравнения (13.15.) по А, Т1, Т2, преобразовав, окончательно получим

где А – погрешность прямого измерения длины,
Т1 и Т2 – погрешность измерения периодов маятников.
![]() ;
;
![]()
t1 и t2 – абсолютная погрешность прямого измерения времени полных колебаний.
Все измерения и расчеты запишите в заранее подготовленную таблицу.
Таблица 13.1.
