направляющими косинусами вектора u.

Теорема 1. Направляющие косинусы являются координатами единичного вектора u ={ux , uy , uz }, заданного в прямоугольной системе координат.

Доказательство. Теорема непосредственно вытекает из определения скалярного произведения. С одной стороны,

Доказательство. По определению, длина единичного вектора равна 1: | u |2 = ux2 +u2y +uz2 =1.

Применяя Теорему 1, получаем требуемый результат.

В заключение заметим, что для произвольного ненулевого вектора a

отношение aa представляет собой единичный вектор и, следовательно,

10. Векторное произведение векторов

Векторное произведение векторов a ={ax , ay , az } и b ={bx ,by ,bz } , заданных в прямоугольной системе координат, представляет собой вектор, определяемый формулой

где i, j и k – ортонормированные базисные векторы.

Часто используется также обозначение векторного произведения в виде [a,b].

Разлагая определитель (14) по элементам первой строки, получаем

19

a ×b = (aybz −azby )i +(azbx −axbx ) j +(axby −aybx )k .

Теорема. Для любых непараллельных друг другу векторов a и b

1)векторное произведение c = a ×b является вектором перпендикулярным к a и b,

a ×b a и a ×b b .

2)Длина вектора c = a ×b равна произведению длин векторов на синус угла между ними,

c= absinθ .

3)Упорядоченный набор векторов {a, b, c} образует правую тройку (как это показано на рисунке).

Доказательство. Выберем такую систему координат, чтобы векторы a и b лежали в плоскости x,y, а вектор a был бы направлен вдоль положительного направления оси x.

Тогда a ={a, 0, 0} и b ={bcosθ, bsinθ, 0} , что влечет за собой

Таким образом, длина вектора | c |= a sinθ , а его направление совпадает с

положительным направлением оси z, т.е. является перпендикулярным к плоскости x,y, в которой лежат векторы a и b.

10.1.Свойства векторного произведения

1)Векторное произведение антикоммутативно:

a ×b = −b ×a . 2) Векторное произведение дистрибутивно:

20

(a +b) ×c = a ×c +b ×c .

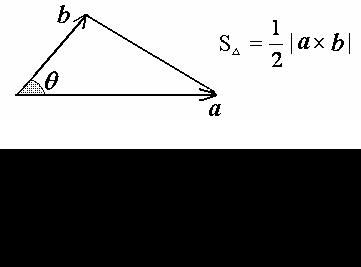
3) Длина вектора c = a ×b равна площади параллелограмма, построенного на векторах a и b .

Следствие. Площадь треугольника, сторонами которого являются векторы a и b , выражается формулой

4) Векторное произведение коллинеарных векторов равно нулю.

Свойства 1) и 2) вытекают из свойств определителей. Действительно,

Свойство 3) следует из Теоремы о векторном произведении. Свойство 4) является совершенно очевидным.

На практике векторное произведение применяется в основном для нахождения площадей треугольников и параллелограммов, а также для построения вектора, перпендикулярного двум заданным векторам.

21

10.2.Примеры

1)Покажем, что базисные векторы i = {1, 0, 0}, j = {0, 1, 0} и k = {0, 0, 1} прямоугольной системы координат выражаются друг через друга с помощью векторного произведения.

Таким образом,

i × j = k , k ×i = j , j ×k = i .

2)Выразить векторное произведение векторов p и q через векторы a и b,

если p = a + b и q = a – b.

Решение.

p ×q = (a +b) ×(a −b)

=a ×a −a ×b +b ×a - b ×b = 2b ×a.

3)Найти площадь треугольника ABC с вершинами в точках A(1, 0, –2),

B(1, 5, 0) и C(0, 4, –1).

Решение. Введем два вектора,

→

a = AB ={0, 5, 2}

и

22