
- •Е. В. АСТАХОВА
- •Барнаул 2012
- •Вопросы для самоконтроля
- •Вопросы для самоконтроля
- •Вопросы для самоконтроля
- •Вопросы для самоконтроля
- •Вопросы для самоконтроля
- •Вопросы для самоконтроля
- •Определение таблиц базы данных
- •Определение полей таблиц
- •Задание индивидуального значения полям таблицы
- •Определение связей между таблицами
- •Алгоритм построения отчета
- •Вопросы для самоконтроля
- •Требования к представлению информации на слайдах
- •Вопросы для самоконтроля

ЛАБОРАТОРНАЯ РАБОТА № 2
АЛГЕБРА ЛОГИКИ
ЗАДАНИЕ 1. |
ФОРМАЛИЗАЦИЯ ВЫСКАЗЫВАНИЙ..................................................................................... |
28 |
ЗАДАНИЕ 2. |
РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ............................................................................................ |
30 |
ЗАДАНИЕ 3. |
АНАЛИЗ ЛОГИЧЕСКОГО ВЫРАЖЕНИЯ ............................................................................... |
32 |
ЗАДАНИЕ 4. |
ПОСТРОЕНИЕ ЛОГИЧЕСКОЙ ВЕНТИЛЬНОЙ СХЕМЫ.................................................... |
32 |
ВПРОЦЕССЕ ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ ФОРМИРУЮТСЯ СЛЕДУЮЩИЕ УМЕНИЯ И НАВЫКИ:
1.Составлять формулы с помощью логических переменных и символов логических операций.
2.Представлять логические выражения в форме таблиц истинности.
3.Решать логические задачи табличным способом.
4.Осуществлять анализ логических выражений.
5.Реализовывать логические выражения в виде вентильных схем.
6.Исследовать формулу на тождественную истинность/ложность, выполнимость.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.Привести примеры логических связок.
2.Какой приоритет имеют логические операции?
3.Как определяется термин «высказывание»?
4.Сколько может быть выходов у логических элементов И, ИЛИ, НЕ?
5.Что позволяет определить анализ логического выражения?
6.Сколько выходов может быть у вентилей?
7.Какие формулы называются выполнимыми?
8.Верно ли, что любое по сложности логическое высказывание можно записать в виде цепочки базовых логических операций?
9.Сколько значений может принимать выходной сигнал?
10.Как узнать, какой базовый логический элемент был использован, если известны значения его входов и выхода?
27

ОСНОВНЫЕ ПОНЯТИЯ
Алгебра логики (Булева алгебра) – это область математики. Она оперирует величинами, которые могут принимать два значения.
Булевыми величинами (или булевыми константами) называются два заранее выбранных разных символа. Например: 0,1; false,true; ложь,истина
Логические (булевы) переменные – это переменные, которые могут принимать булевы значения.
Логическими функциями (булевыми функциями) называются функции, аргументами которых могут быть либо булевы величины, либо булевы переменные.
Функции в булевой алгебре принято определять двумя способами: с
помощью таблиц истинности и в виде формул.
В таблице истинности перечислены все возможные комбинации параметров и результат функции для каждой из комбинаций.
Замечание. Добавление одной новой переменной увеличивает число сочетаний ровно в два раза. Общее число сочетаний равно 2N, где N – число переменных.
В формулах применяются знаки унарных и бинарных операций. Знак унарной операции обозначает функцию от одного аргумента f(x). Знак бинарной операции обозначает функцию от двух аргументов g(x,y).
БЛОК ОСНОВНЫХ ЗАДАНИЙ
ЗАДАНИЕ 1. ФОРМАЛИЗАЦИЯ ВЫСКАЗЫВАНИЙ
Формализовать высказывания с помощью логических переменных и символов логических операций.
НАЧАЛЬНЫЙ УРОВЕНЬ
1.Студент защитил все лабораторные работы и написал тест.
2.Выпускник школы решил поступать в вуз или в колледж.
3.Студент встал поздно и не пошел на занятия.
БАЗОВЫЙ УРОВЕНЬ
1.Если защитить все лабораторные работы и написать тест, то можно набрать
75балов.
2.Если защищать лабораторную работу без отчета или не написать контрольный тест, то теряется возможность получить «автомат».
ПОВЫШЕННЫЙ УРОВЕНЬ
1.Если защитить все лабораторные работы, написать тест и не пропускать занятия, то можно набрать 75 балов, а это означает возможность получить «автомат».
2.Если пропустить лекцию и не написать реферат, то из рейтинга вычитаются
6баллов, а значит, в итоге можно не дотянуть до «автомата».
28

3.Если при защите лабораторных блеснуть дополнительными знаниями, то можно заработать дополнительно 5 баллов, следовательно, повысить семестровый рейтинг и может быть заработать «автомат».
4.Если пропускать занятия или вовремя не отрабатывать пропуски, то к концу семестра можно «утонуть» в долгах и не выйти на сессию.
СПРАВОЧНЫЙ МАТЕРИАЛ
Логическое высказывание – это повествовательное предложение, про которое можно однозначно сказать, истинно оно или ложно.
Алгебра логики рассматривает любое высказывание только с позиции его истинности или ложности.
Логические связки – это слова и словосочетания «не», «и», «или», «если …, то», «тогда и только тогда» и т.п.
Логические связки позволяют из элементарных высказываний строить новые составные высказывания.
Пример 1. Элементарные высказывания «Иванов – студент», «Иванов
– футболист». Связка «И» позволяет получить составное высказывание «Иванов – студент, хорошо играющий в футбол».
Истинность составного высказывания зависит от истинности или ложности элементарных высказываний.
Для обращения к высказываниям им назначают имена.
Пример 2. Обозначим первое высказывание из примера 1 через А, второе – через В. Тогда составное высказывание можно кратко записать как А и В. Здесь А, В – логические переменные, которые могут принимать значения «истина» (1) или «ложь» (0).
Логические связки рассматриваются как операции над логическими высказываниями.
Обозначения логических операций НЕ (черта над высказыванием, ¬) – отрицание (инверсия). Инверсия
истинна, когда высказывание ложно. Например, «6 делится на 2» (А); «6 не делится на 2» (¬А).
И( , , &) – логическое умножение (конъюнкция). Высказывание
АВ истинно тогда и только тогда, когда истинны оба элементарных высказывания. Например, для составного высказывания «6 делится на 2 » (А)
И«6 делится на 3» (В) возможны 4 исхода:
1). «6 делится на 2 » И «6 делится на 3» – истинно;
2)«6 делится на 2 » И «6 не делится на 3» – ложно;
3)«6 не делится на 2 » И «6 делится на 3» – ложно;
4)«6 не делится на 2 » И «6 не делится на 3» – ложно.
ИЛИ (+, ) – логическое сложение (дизъюнкция). Высказывание А В ложно тогда и только тогда, когда ложны оба элементарных высказывания. Например, для составного высказывания «6 делится на 2 » (А) И «6 делится на 3» (В) возможны 4 исхода:
29

1). «6 делится на 2 » ИЛИ «6 делится на 3» – истинно;
2)«6 делится на 2 » ИЛИ «6 не делится на 3» – истинно;
3)«6 не делится на 2 » ИЛИ «6 делится на 3» – истинно;
4)«6 не делится на 2 » ИЛИ «6 не делится на 3» – ложно;
ЕСЛИ-ТО (→) – импликация. Высказывание А → В ложно тогда и только тогда, когда А истинно, а В ложно. Например, «четырехугольник является квадратом» (А); «данный четырехугольник нельзя вписать в окружность» (В).
Импликацию можно выразить через дизъюнкцию и отрицание
А → В = ¬А В.
РАВНОСИЛЬНО (≡, ↔, ~) – эквиваленция (равносильность, двойная импликация, равноистинность). Высказывание А ↔ В истинно тогда и только тогда, когда значения А и В совпадают. Например, «треугольник является прямоугольным» (А) равносильно тому, что «сумма квадратов катетов равна квадрату гипотенузы» (В).
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию: А ↔ В = (¬А В) (¬B А).
Замечание. Логические функции эквивалентны, если совпадают их таблицы истинности.
НЕРАВНОЗНАЧНОСТЬ ( ) – (сложение по модулю 2,
исключающее ИЛИ). Высказывание А ↔ В истинно тогда и только тогда,
когда значения А и В совпадают. |
|
|
1 X = ¬X |
0 X = X |
X ¬X = 1 |
Следствие. X X X ……. X = X – при нечетном числе членов, 0 – при четном.
Замечание. В логических операциях причинно-следственные связи между высказываниями не учитываются. Высказывания могут быть совершенно не связаны по содержанию, рассматривается только их истинность или ложность. Например, «Если студент получил пятерку, то на улице хорошая погода»; «Чтобы получить пятерку необходимо и
достаточно, чтобы на улице была хорошая погода». |
|
||
Приоритет выполнения логических операций: |
|
||
1. отрицание |
2. конъюнкция |
3. дизъюнкция |
4. импликация |
Формализация высказывания заключается в замене его логической формулой, составленной из логических переменных и символов логических операций.
ЗАДАНИЕ 2. РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ
1.Формализовать логическую задачу. Записать формульное выражение.
2.Решить задачу табличным способом.
30

НАЧАЛЬНЫЙ УРОВЕНЬ
Спор болельщиков о результатах скачек. Петя: Выиграет Алмаз или Гранат. Вася: Первым будет Верный.
Коля: Или Верный, или Алмаз.
В итоге оказался прав один из друзей. Кто дал верный прогноз?
БАЗОВЫЙ УРОВЕНЬ
Спор болельщиков о результатах скачек.
Петя: Выиграет Алмаз. Пират никогда не приходил первым.
Вася: У Пирата лучше данные – он будет первым. А на Алмаза я бы не ставил.
Коля: Точно, Алмазу не видать первого места. Победит Пират.
В итоге оказался прав один из друзей. Кто из лошадей победил в забеге?
ПОВЫШЕННЫЙ УРОВЕНЬ
Спор болельщиков о результатах скачек. Петя: Выиграет Алмаз. Пират будет вторым.
Вася: У Пирата лучше данные – он будет первым. А на Алмаза лучше не ставить.
Коля: Я тоже за победу Пирата. Алмазу не видать первого места.
В итоге оказались правы двое из друзей. Кто из лошадей победил в забеге?
СПРАВОЧНЫЙ МАТЕРИАЛ
Таблица истинности – это один из способов вычислений в формальной логике. Таблица позволяет определить истинность какого-нибудь сложного логического высказывания по истинности его фрагментов.
В каждой строке таблицы слева перечисляются параметры, а в крайнем правом столбце – результат. В верхней строке – обозначения параметров и обозначение функции. Варианты перебираются в таком порядке, что цифры во всех столбцах, кроме самого правого представляют собой обычный натуральный ряд: 0, 1, 2, 3, 4, 5,.. но в двоичной системе счисления: 000, 001, 010, 011, 100, 101.
Булева функция N переменных полностью определяется таблицей из 2N строк.
Таблица истинности используется для описания работы логических элементов И, ИЛИ, НЕ и логических формул, построенных из этих элементов. В таблице перечислены все возможные сочетания входных значений операндов и выходного значения для каждого сочетания.
Х |
У |
Х У |
|
Х |
У |
Х У |
|
Х |
¬Х |
|
0 |
0 |
0 |
|
0 |
|
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
|
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
|
0 |
1 |
|
|
|
1 |
1 |
1 |
|
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
31 |
|
|
|
|
|

При нахождении значений формулы в таблицу истинности кроме значений переменных вносят и значения промежуточных формул.
Пример. Таблица истинности для формулы х у ¬(х у) х
Переменные |
|
Промежуточные формулы |
Формула |
|||
х |
у |
х у |
х у |
¬(х у) |
(х у) (¬(х у)) |
х у ¬(х у) х |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
ЗАДАНИЕ 3. АНАЛИЗ ЛОГИЧЕСКОГО ВЫРАЖЕНИЯ
Определить наборы значений входных сигналов, при которых выходной сигнал примет значение «ложь».
НАЧАЛЬНЫЙ УРОВЕНЬ
¬x y
БАЗОВЫЙ УРОВЕНЬ
(x y) → ¬x
ПОВЫШЕННЫЙ УРОВЕНЬ
¬(x y) z
СПРАВОЧНЫЙ МАТЕРИАЛ
Таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы с двумя переменными существует 4 набора значений переменных (22 = 4): (0,0), (0,1), (1,0), (1,1).
Для формулы с тремя переменными – 8 наборов (23 = 8): (0,0,0), (0,0,1), (0,1,0), (1,0,0), (0,1,1), (1,0,1), (1,1,0), (1,1,1).
ЗАДАНИЕ 4. ПОСТРОЕНИЕ ЛОГИЧЕСКОЙ ВЕНТИЛЬНОЙ СХЕМЫ
Для логических выражений построить вентильные схемы.
НАЧАЛЬНЫЙ УРОВЕНЬ
¬x y z
БАЗОВЫЙ УРОВЕНЬ
(x y) ¬x
ПОВЫШЕННЫЙ УРОВЕНЬ
¬(x y) ¬(x z)
32

СПРАВОЧНЫЙ МАТЕРИАЛ
Логический элемент компьютера представляет электронную логическую схему, которая реализует элементарную логическую функцию. Например, схемы (вентили) И, ИЛИ, НЕ. С помощью базовых схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Количество входов у вентилей бывает от одного до восьми и один выход.
|
Х |
|
Элементарная |
Выходной сигнал |
Входные |
Х |
|
логическая |
F(Х1, Х2,….., Хn) |
|
||||
сигналы |
|
… |
функция |
|
Х |
|
|||
|
|
|
|
|
|
|
|
|
Для реализации схем И-НЕ, ИЛИ-НЕ используют графическое изображение инвертора на выходе.
|
Входные |
|
|
Х |
|
|
|
|
Логическая |
|
|
Выходной сигнал |
||||||
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
сигналы |
|
|
|
|
|
|
|
|
функция |
|
|
|
¬F(Х1, Х2,….., Хn) |
||||
|
|
|
|
|
… |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Вентильная схема для логического выражения ¬(X Y Z F) |
||||||||||||||||||
Вариант 1. |
|
|
|
|
|
|
|
|
Вариант 2. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
И |
|
|
|
|
|
|
|
|
X |
|
И |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Y |
|
|
|
ИЛИ |
|
|
|
|
|
Y |
|
|
|
|
ИЛИ- |
|
||
|
|
|
|
|
НЕ |
|
|
|
|
|
|
|||||||
Z |
|
|
|
|
|
|
|
|
Z |
|
|
|
|
НЕ |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
||
БЛОК ВАРИАТИВНЫХ ЗАДАНИЙ
ЗАДАНИЕ 1. ИССЛЕДОВАНИЕ ФОРМУЛЫ
С помощью таблиц истинности исследовать формулу на тождественную истинность (ложность) по варианту.
Вариант 1. ¬(¬x x) y (x y y) Вариант 2. a b (c ¬e d) ¬b Вариант 3. x (y (¬x ¬y))
Вариант 4. ¬((¬x y) (¬y z)) ¬x z Вариант 5. (¬x ¬y) (¬y z)) x
33

СПРАВОЧНЫЙ МАТЕРИАЛ
Формула называется выполнимой, если она при некоторых значениях переменных принимает значение «истина», а при некоторых – значение «ложь».
Формула называется тождественно истинной (тавтологией), если она при всех значениях переменных принимает значение «истина». Например, формула А ¬А для высказывания «Этот угол прямой или косой».
Формула называется тождественно ложной (противоречием), если она при всех значениях переменных принимает значение «ложь». Например, формула А ¬А для высказывания «Это дерево самое высокое в саду, но есть деревья выше».
ЗАДАНИЕ 2. ПРЕОБРАЗОВАНИЯ ФОРМУЛ
Упростить логические выражения по варианту.
Вариант 1. z y x z y x
Вариант 2. x z x y x z y
Вариант 3. x y z x y x y x y z
Вариант 4. x y z x y x y
Вариант 5. y x → (x → y x)
СПРАВОЧНЫЙ МАТЕРИАЛ
Логические операции НЕ, И, ИЛИ относятся к базовым. Любые логические формулы могут выражены через базовые операции.
Логические функции имеют много свойств, позволяющих выполнять различные преобразования.
Правила преобразований записываются в виде равенств:
F = G, где F и G – булевы функции, заданные в виде формул с унарными и бинарными операциями.
Такая запись означает: если в обеих частях равенства вместо переменных подставить любые константы и проделать вычисления, то в результате получатся одинаковые результаты: 0 = 0 или 1 = 1.
Замечание Равенства не арифметические, поэтому нельзя переносить переменные из одной части равенства в другую с обратным знаком.
34

Правила вывода
1.Если в обоих частях равенства заменить переменную на любую формулу (одну и ту же во всех местах, где встречается эта переменная), то получится равенство.
2.Если F = G, то в любом равенстве можно заменять F на G или G на F
ив результате получится равенство. Делать замену во всех местах необязательно.
Основные законы (аксиомы) булевой алгебры
1.¬(¬X) = Х
2.X Y = Y Х; X Y = Y Х
3.(X Y) Z = X (Y Z) = X Y Z (X Y) Z = X (Y Z) = X Y Z
4.X X = X; X X = X
5.X (X Y) = Х; X (X Y) = Х
6.X (Y Z) = (X Y) (X Z) X (Y Z) = (X Y) (X Z)
7.¬(X Y) = ¬X¬Y ¬(X Y) = ¬X¬Y
8.X (Y¬Y) = Х X (Y¬Y) = Х
9.¬0 = 1; ¬1 = 0;
Двойное отрицание Коммутативность
Ассоциативность
Идемпотентность
Поглощение
Дистрибутивность
Моргана (перенесение бинарной операции на операнды)
Нейтральность Существование единицы
¬Х Х = 1; ¬Х Х = 0 |
|
|
|
Из аксиом можно вывести ряд полезных соотношений: |
|
||
Х 1 = Х |
Х 0 = 0 |
Х 0 = Х |
Х 1 = 1 |
Способы упрощения выражения
Перестановка операндов
Операции, допускающие перестановку операндов без изменения истинности:
X Y = Y X
X 


 Y = Y
Y = Y 

 X
X
X 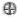 Y = Y
Y = Y  X
X
X 


 Y = Y
Y = Y 


 X
X
Избавление от скобок
Ассоциативность означает, что не обязательно писать скобки, когда подряд идут одинаковые операции, поскольку порядок вычисления не повлияет на результат. Например, можно написать X Y Z вместо
X (Y Z) или (X Y) Z.
35

Вынесение за скобки
Свойство "дистрибутивности" позволяет выносить за скобку одинаковые операнды.
Примеры.
1.(X Y) 


 (X Z) = X (Y
(X Z) = X (Y 

 Z)
Z)
2.(X Z) 


 (Y Z) = (X
(Y Z) = (X 

 Y) Z
Y) Z
3.(X 


 Y) (X
Y) (X 

 Z) = X
Z) = X 

 (Y Z)
(Y Z)
4.(X 


 Z) (Y
Z) (Y 


 Z) = (X Y)
Z) = (X Y) 

 Z
Z
5.(X Y)  (X Z) = X (Y
(X Z) = X (Y  Z)
Z)
6.(X Z)  (Y Z) = (X
(Y Z) = (X  Y) Z
Y) Z
Избавление от отрицаний
Закон двойного отрицания и законы Де Моргана позволяют избавляться от лишних знаков отрицания, а также заменять одни операции другими, добавляя лишние знаки отрицания.
Примеры.
1.¬(¬X) = X
2.¬(X  Y) = X
Y) = X 


 Y
Y
3.¬(X 


 Y) = X
Y) = X 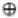 Y
Y
4.¬(¬X ¬Y) = X 

 Y
Y
5.¬(¬X 

 ¬Y) = X Y
¬Y) = X Y
6.¬(X Y) = ¬X 


 ¬Y
¬Y
7.¬(X 

 Y) = ¬X ¬Y
Y) = ¬X ¬Y
Законы поглощения
Законы поглощения позволяют упрощать логические выражения, в которых встречаются операнды 1 (истина), 0(ложь), повтор операнда или его отрицание.
Действие |
Повторы операнда |
|
Отбрасывание повторов |
X X = X |
X & X = X |
0 |
X |
X = 0 |
1 |
X X = 1 |
X X = 1 |
Действие |
Комбинации 1 с логическими операциями |
|||||
Отрицание |
X 1 = ¬X |
1 |
X = ¬X |
¬X 1 = X |
1 |
¬X = X |
операнда |
|
|
|
|
|
|
Отбрасывание 1 |
X 1 = X |
1 X = X |
¬X 1 = ¬X |
1 ¬X = ¬X |
||
|
|
|
|
¬X 1 = ¬X |
|
|
|
X 1 = X |
1 |
X = X |
1 |
¬X = ¬X |
|
1 |
X 1 = 1 |
1 |
X = 1 |
¬X 1 = 1 |
1 |
¬X = 1 |
Отбрасывание |
X 1 = 1 |
1 |
X = X |
¬X 1 = 1 |
1 |
¬X = ¬X |
левого |
|
|
|
|
|
|
операнда |
|
|
|
|
|
|
|
|
|
36 |
|
|
|

Действие |
Комбинации 0 с логическими операциями |
|||||
Отбрасывание 0 |
X 0 = X |
0 |
X = X |
¬X 0 =¬X |
0 |
¬X =¬X |
|
X 0 = X |
0 |
X = X |
¬X 0 =¬X |
0 |
¬X =¬X |
0 |
X 0 = 0 |
0 X = 0 |
¬X 0 = 0 |
0 ¬X = 0 |
||
Отрицание |
X 0 = ¬X |
0 |
X = ¬X |
¬X 0 = X |
0 |
¬X = X |
операнда |
|
|
|
|
|
|
Отрицание левого |
X 0 = ¬X |
0 |
X = 1 |
¬X 0 = X |
0 |
¬X = 1 |
операнда |
|
|
|
|
|
|
Действие |
Комбинации отрицания с логическими операциями |
|||
1 |
X ¬X = 1 |
¬X X = 1 |
X ¬X =1 |
¬X X =1 |
|
|
|
|
|
0 |
X ¬X = 0 |
¬X X = 0 |
X ¬X =0 |
¬X X =0 |
Отбрасывание |
|
|
|
|
левого |
X ¬X = ¬X |
¬X X =X |
||
операнда |
|
|
|
|
Приведение подобных членов
Законы приведения подобных членов позволяют объединять две формулы в одну с упрощением ее вида.
Если к формуле вида X Y добавить еще раз один из ее операндов через 

 , то можно совсем отбросить другой операнд.
, то можно совсем отбросить другой операнд.
(X Y) 

 X = X X
X = X X 

 (X Y) = X (X Y)
(X Y) = X (X Y) 

 Y = Y Y
Y = Y Y 

 (X Y) = Y
(X Y) = Y
Если к формуле вида X Y добавить отрицание одного из ее операндов через 


 , то можно убрать этот операнд без отрицания.
, то можно убрать этот операнд без отрицания.
(X Y) |
¬X = ¬X Y |
¬X (X Y) = ¬X Y |
(X Y) |
¬Y = X ¬Y |
¬Y (X Y) = X ¬Y |
Если в формуле вида X Y один из операндов содержит отрицание и добавить его без отрицания через 

 , то можно убрать отрицание.
, то можно убрать отрицание.
(¬X Y) X = X Y |
X (¬X Y) = X Y |
(X ¬Y) Y = X Y |
Y (X ¬Y) = X Y |
Обобщенное правило приведения подобных членов: Операнд в скобках, похожий на операнд за скобками, всегда убирается. Если они совпадают, то убирается и оставшийся операнд в скобках.
Тавтологии для импликации
(X  Y) = (X
Y) = (X 

 ¬Y) (X
¬Y) (X  Y) (Y
Y) (Y  X) = (X
X) = (X 


 Y) (X
Y) (X  Y)
Y) 


 (¬Y
(¬Y  ¬X)
¬X)
Пример.
Тавтология X Y 


 Y X позволяет заменять в любой формуле X Y на Y X, получая равноистинную формулу.
Y X позволяет заменять в любой формуле X Y на Y X, получая равноистинную формулу.
Так, формулу ¬ (X Y) 

 Z можно изменить на формулу ¬ (Y X)
Z можно изменить на формулу ¬ (Y X) 

 Z
Z
37
