
- •Вариант 1.
- •Вариант 2.
- •Вариант 3.
- •Вариант 4.
- •Вариант 5.
- •Вариант 6.
- •Вариант 7.
- •Вариант 8.
- •Вариант 9.
- •Вариант 10.
- •Вариант 11.
- •Вариант 12.
- •Вариант 13.
- •Вариант 14.
- •Вариант 15.
- •Вариант 16.
- •Вариант 17.
- •Вариант 18.
- •Вариант 19.
- •Вариант 20.
- •Вариант 21.
- •Вариант 22.
- •Вариант 23.
- •Вариант 24.
- •Вариант 25.
- •Вариант 26.
- •Вариант 27.
- •Вариант 28.
- •Вариант 29.
- •Вариант 30.
Вариант 17.
По определению вычислить производную функции в точке
 :
:
а)
![]() ;
б)
;
б)![]() .
.
Найти производные функций:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в) ;
г)
;
г)![]() ;
;
д)
![]() ;
е)
;
е)![]() ;
ж)
;
ж) ;
з)
;
з)![]() ;
;
и)
![]() ;
к)
;
к)![]() .
.
Найти производную функции
 в точках
в точках .
.Вычислить производную сложной функции:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
;
е)
 ;
ж)
;
ж)
![]() ;
з)
;
з)
 .
.
Логарифмическое дифференцирование:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в) .
.
Найти производные функций, заданных неявно:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Найти производные функций, заданных параметрически:
а)
 ;
б)
;
б) ;
в)
;
в) .
.
Найти производные второго порядка заданных функций:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Выяснить, в каких точках кривой
 касательная
составляет с осьюOX
угол
касательная
составляет с осьюOX
угол
 .
.По оси OX движутся две материальные точки, законы движения которых
 и
и .
В какой момент времени их скорости
окажутся равными?
.
В какой момент времени их скорости
окажутся равными?
ТИПОВОЙ РАСЧЕТ по теме
“ТЕХНИКА ДИФФЕРЕНЦИРОВАНИЯ”
Вариант 18.
По определению вычислить производную функции в точке
 :
:
а)
![]() ;
б)
;
б)![]() .
.
Найти производные функций:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
;
д)
![]() ;
е)
;
е)![]() ;
ж)
;
ж)![]() ;
з)
;
з)![]() ;
;
и)
 ;
к)
;
к)![]() .
.
Найти производную функции
 в точках
в точках
Вычислить производную сложной функции:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)![]() ;
д)
;
д)
 ;
е)
;
е)
![]() ;
;
ж)
![]() ;
з)
;
з)
 .
.
Логарифмическое дифференцирование:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в) .
.
Найти производную функций, заданных неявно:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Найти производные функций, заданных параметрически:
а)
 ;
б)
;
б) ;
в)
;
в)![]() .
.
Найти производные второго порядка заданных функций:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в) .
.
Выяснить, в какой точке кривой
 касательная
составляет с осьюOXугол
касательная
составляет с осьюOXугол .
.Закон движения материальной точки
 .
В какой момент времени ее скорость
будет равна 10 м/с?
.
В какой момент времени ее скорость
будет равна 10 м/с?
ТИПОВОЙ РАСЧЕТ по теме
“ТЕХНИКА ДИФФЕРЕНЦИРОВАНИЯ”
Вариант 19.
По определению вычислить производную функции в точке
 :
:
а)
![]() ;
б)
;
б)![]() .
.
Найти производные функций:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в) ;
г)
;
г)![]() ; д)
; д) ;
;
е)
 ;
ж)
;
ж)![]() ;
з)
;
з) ;
и)
;
и)![]() ;
;
к)![]() .
.
Найти производную функции
 в точках
в точках .
.Вычислить производную сложной функции:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
;
е)
![]() ;
ж)
;
ж)
 ;
з)
;
з)
 .
.
Логарифмическое дифференцирование:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Найти производную функций, заданных неявно:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Найти производные функций, заданных параметрически:
а)
 ;
б)
;
б) ;
в)
;
в) .
.
Найти производные второго порядка заданных функций:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в) .
.
Выяснить, в какой точке кривой
 касательная
составляет с осьюOXугол
касательная
составляет с осьюOXугол .
.Материальная точка движется по гиперболе
 так, что ее абсциссаxравномерно возрастает со скоростью 1
м/с. С какой скоростью изменяется
ордината точки, когда она проходит
положение (4, 5)?
так, что ее абсциссаxравномерно возрастает со скоростью 1
м/с. С какой скоростью изменяется
ордината точки, когда она проходит
положение (4, 5)?
ТИПОВОЙ РАСЧЕТ по теме
“ТЕХНИКА ДИФФЕРЕНЦИРОВАНИЯ”
Вариант 20.
По определению вычислить производную функции в точке
 :
:
а)
![]() ;
б)
;
б)![]() .
.
Найти производные функций:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в) ;
г)
;
г)![]() ;
;
д)
![]() ;
е)
;
е)![]() ;
ж)
;
ж)![]() ;
з)
;
з) ;
;
и)
![]() ;
к)
;
к) .
.
Найти производную функции
 в точках
в точках .
.Вычислить производную сложной функции:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
;
е)
![]() ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() .
.
Логарифмическое дифференцирование:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в) .
.
Найти производную функций, заданных неявно:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Найти производные функций, заданных параметрически:
а)
 ;
б)
;
б) ;
в)
;
в) .
.
Найти производные второго порядка заданных функций:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в) .
.
Выяснить, в каких точках кривой
 касательная
составляет с осьюOXугол
касательная
составляет с осьюOXугол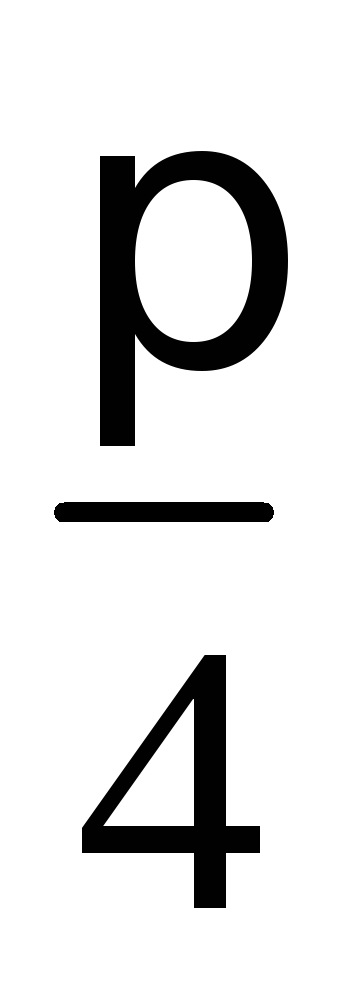 .
.В какой точке параболы
 ордината возрастает вдвое быстрее, чем
абсцисса?
ордината возрастает вдвое быстрее, чем
абсцисса?
ТИПОВОЙ РАСЧЕТ по теме
“ТЕХНИКА ДИФФЕРЕНЦИРОВАНИЯ”
