Применение закона Харди-Вайнберга

Одно из важнейших применений закона Харди-Вайнберга состоит в том, что он дает возможность рассчитать некоторые из частот генов и генотипов в том случае, когда не все генотипы могут быть идентифицированы вследствии доминантности некоторых аллелей.

Пример 1: альбинизм у человека обусловлен редким рецессивным геном. Если аллель нормальной пигментации обозначить А, а аллель альбинизма а, то генотип альбиносов будет аа, а генотипы нормально пигментированных людей – АА и Аа. Предположим, что в популяции людей (Европейской части) частота альбиносов составляет 1 на 10000. Согласно закону Харди-Вайнберга, в данной популяции частота гомозигот q²аа=1:10000=0,0001 (0,1%), а частота рецессивных гомозигот =0,01. Частота доминантного аллеля рА=1-qa=1-0,01=0,99. Частота нормально пигментированных людей составляет р²АА=0,99²=0,98(98%), а частота гетерозигот 2pqАа=20,990,1=0,198(1,98%).

Важное следствие из закона Харди-Вайнберга состоит в том, что редкие аллели присутствуют в популяции главным образом в гетерозиготном состоянии. Рассмотрим приведенный пример с альбинизмом (генотип аа). Частота альбиносов равна 0,0001, а гетерозигот Аа 0,00198. Частота рецессивного аллеля у гетерозигот составляет половину частоты гетерозигот, т.е. 0,0099. Следовательно, в гетерозиготном состоянии содержится примерно в 100 раз больше рецессивных аллелей, чем в гомозиготном состоянии. Таким образом, чем ниже частота рецессивного аллеля, тем большая доля этого аллеля присутствует в популяции в гетерозиготном состоянии.

Пример 2: частота фенилкетонурии (ФКУ) в популяции составляет 1:10000, ФКУ – аутосомно-рецессивное заболевание, следовательно индивидуумы с генотипами АА и Аа – здоровы, с генотипами аа – больны ФКУ.

Популяция, следовательно представлена генотипами в следующем соотношении:

p²AA+2pqAa+q²aa=1

? ? ? = 10000.

Исходя их этих условий:

q²aa=1/10000=0,0001.

pA=1-qa=1-0,01=0,99

p²AA=0,99²=0,9801

2paAa=20,990,01=0,0198, или 1,98% (2%)

Следовательно в данной популяции частота гетерозигот по гену ФКУ по изучаемой популяции составляет приблизительно 2%. Количество индивидумов с генотипом АА составляет 100000,9801=9801, количество индивидуумов с генотипом Аа (носителей) составляет 100000,0198=198 человек, т.к. относительные доли генотипов в этой популяции представлены соотношением 1(аа):198(Аа):980 (АА).

В том случае, если ген в генофонде представлен несколькими аллелями, например ген I группы крови системы АВ0, то соотношение различных генотипов выражается формулой (и принцип Харди-Вайнберга остается в силе.

Например: среди Египтян встречаются группы крови в системе АВ0 в следующем процентном соотношении:

0(I) - 27,3%, A(II) - 38,5%, B(III) - 25,5%, AB(IV) - 8,7%

Определить частоту аллелей I⁰, I^A, I^B и разных генотипов в этой популяции.

При решении задачи можно воспользоваться формулами:

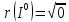; (;, где А – частота группы крови А (II); 0 – частота группы крови 0(I); В – частота группы крови В(III).

; (;

Проверка: pI^A+qI^B+rI⁰=1 (0,52+0,28+0,20=1).

Для генов, сцепленных с полом, равновесие частоты Х^А₁Х^А₁, Х^А₁Х^А₂ и Х^А₂Х^А₂ совпадают с таковыми для аутосомных генов: p²+2pq +q². Для самцов (в случае гетерогаметного пола) в силу гемизиготности возможны лишь два генотипа Х^А₁Y или Х^А₂Y, которые воспроизводятся с частотой равной частоте соответствующих аллелей у самок в предшествующем поколении: p и q. Из этого следует, что фенотипы, определяемые рецессивными аллелями сцепленных с Х-хромосомой, у самцов встречаются чаще, чем у самок. Так, при частоте аллеля гемофилии qa=0,0001, у мужчин заболевание встречается в 10000 раз чаще, чем у женщин (1/10000млн. у мужчин и 1/100млн. у женщин).

Для установления и подтверждения типа наследования заболеваний необходимо проверить соответствие сегрегации в отягощенных семьях заданной популяции менделеевским закономерностям. Методом -квадрат подтверждает соответствие количества больных и здоровых сибсов для аутосомной патологии в семьях с полной регистрацией (через больных родителей).

Для расчета сегрегационной частоты можно использовать ряд методов: метод сибсов Вайнберга, пробандовый метод.

Задание 1.

Изучите конспект лекций и материал учебной литературы.

Задание 2.

Запишите в словарь и выучите основные термины и понятия: популяция, панмиксия, панмиксная популяция, генофонд, частота аллеля, частота фенотипа и генотипа в популяции, Закон Харди-Вайнбергера (его содержание), генетическая структура популяции, равновесие генетической структуры популяции в поколениях, мутационное давление, генетический груз, коэффициент отбора, популяционно-генетический анализ, факторы генетической динамики популяции, генетический дрейф, инбридинг, адаптационный коэффициент.

Задание 3.

Смоделируйте панмиксную популяцию и сделайте вывод о ее генетической структуре и о генетическом равновесии в ряду поколений (по заданию преподавателя), в двух вариантах, при s=0 и при s=-1аа.

Гаметы условно представлены картонными кружочками. Кружок темного цвета обозначает гамету с доминантным аллелем А, белого – с рецессивным аллелем а. Каждая подгруппа получает по два мешочка, в которых по сто «гамет»: в одном – «яйцеклетки», в другом - «сперматозоиды»: например, А – 30 кружочков, а – 70 кружочков, всего – 100 сперматозоидов и также яйцеклеток. Один из студентов достает, не глядя, по одному кружочку («яйцеклетки»), другой аналогично достает кружки –«сперматозоиды», третий студент записывает полученную комбинацию генотипа в Таблицу 5, используя правило конвертов. Сочетание двух темных кружков означает АА, гомозиготу по доминанту; двух белых аа, гомозиготу по рецессиву; темный и белый – Аа, гетерозиготу. Так как сочетание кружков–гамет случайно, то имитируется процесс панмиксии.

Таблица 5. Число генотипов и частота аллелей в модельной популяции

Поколение	Число генотипов				Всего		χ2		Частота аллелей
	АА	Аа	аа	рА					qА
IвариантS=0 F1 F2 F3
IIвариантS=-1aa F1 F2 F3 F4 F5 F6

Во втором варианте следует выполнять работу до тех пор, пока число генотипов не будет повторяться, что свидетельствует об установлении в популяции нового равновесного состояния.

При записи генотипов могут вкрадываться как случайные ошибки, так и отражаться закономерное изменение числа генотипа. Поэтому необходимо вычислить критерий χ² – критерий соответствия практически полученных данных теоретически ожидаемому.

Для этого определим теоретически ожидаемую частоту генотипов для заданного соотношения гамет. Например, если исходные гаметы: кружки А – 30, а –70; то по таблице Пеннета:

♂ ♀	pА 0,3	qа 0,7
pА 0,3	p2AA 0,09	pqAa 0,21
qa 0,7	pqAa0,21	q2aa 0,49

В этой таблице 0,09 АА – соответствует 9 генотипам АА из 100, 0,42 Аа – соответствует 42 генотипам Аа из 100, 0,49 аа – соответствует 49 генотипам аа из 100 полученных в опыте.

Далее составим таблицу для определения χ² :

Генотипы	Число генотипов
	АА	Аа	Аа	Всего
Допустим, практически полученные (P) (в среднем по 3 поколениям)	12	36	52	100
Теоретически ожидаемые (q)	9	42	49	100
Отклонение (d)	+3	-6	+3
	9	36	9

χ²_факт. = Σd²/q =9:9+36:42+9:49=1 + 0,85 + 0,18 = 2,03 ; при n' =2 , при P =0,05

Сравнив методом χ² полученные результаты с теоретически ожидаемыми делаем вывод, что в данном случае полученное отношение не отличается от ожидаемого, так как χ²_факт. < χ2 табличное 5,99. Следовательно, в I варианте в панмиксной популяции сохраняются первоначальные частоты аллелей (рА – 03 и qa – 0,3). Аналогичную работу проведите для I и II вариантов. Сделайте выводы.

Задание 4.