7. Записывается результат измерения:

(20)

при заданном . Это означает, что с заданной доверительной вероятностьюдоверительный интервалнакрывает, т.е..

8. если необходимо, то находится относительная погрешность, при этом, поскольку Х₀ неизвестно, приближенно его заменяют на:

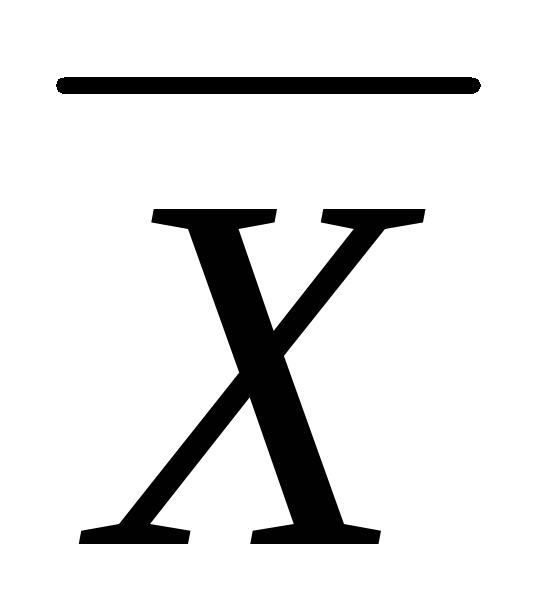. (21)

Методика оценки случайных погрешностей косвенных измерений

Чаще всего интересующая нас величина Х непосредственно не измеряется. Вместо этого измеряются некоторые величины , а затем вычисляется искомая величина Х, которая является функцией указанных непосредственно измеренных величин:

(22)

Для каждой из величин мы находим, как было указано выше, наиболее вероятное значение, т.е. среднеарифметическое из измеренных значений; и оцениваем их погрешности – либо вычисляем их среднеквадратичные погрешностидля случая многократных изменений, либо находим максимальные погрешности, в случае отсутствия разброса в значенияхпри многократных измерениях.

Т.к. каждая из величин - случайна, случайной будет и величинаХ – как функция случайных аргументов. Тогда, очевидно, наиболее близким к истинному значению Х₀ искомой величины будет значение функции:

. (23)

Погрешность результата косвенных измерений зависит от погрешностей прямых измерений каждой из величин, входящих в эту формулу.

Для расчета абсолютной погрешности косвенного измерения при заданной доверительной вероятности следует использовать выражение (даем без вывода):

(24)

где - погрешности прямых измерений при заданной доверительной вероятности(одинаковой для),- частные производные функциипо переменнымсоответственно. Напомним, что частная производная функции нескольких переменныхпо одной из них, например, поu, является обычной производной функции f по u, только при этом другие переменные считаются постоянными параметрами. Все производные в формуле (24) вычисляются при значении

Для нахождения максимальной абсолютной погрешности используют формулу:

(25)

Окончательный результат измерений и вычислений записывается в виде

при заданной доверительной вероятности :

или ,где -максимальная абсолютная погрешность.

При этом обязательно указывать название характеризующей результат меры точности или ). Если необходимо, указывается и значение относительной погрешности

или (26)

Порядок обработки результатов косвенных измерений следующий:

1. находятся средние арифметические 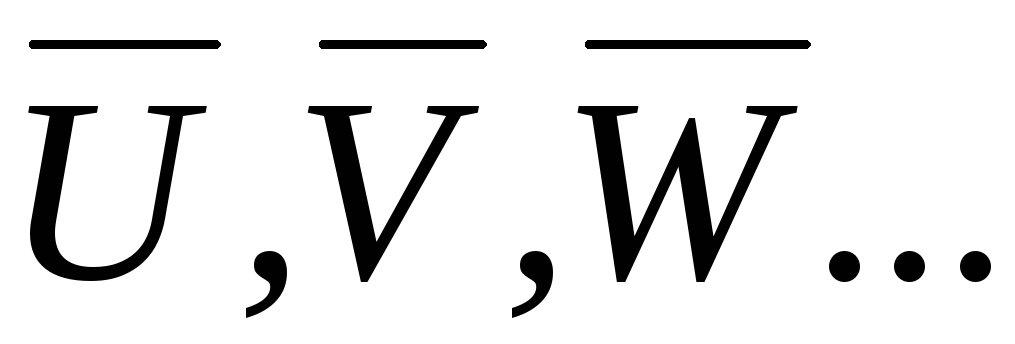и абсолютные погрешности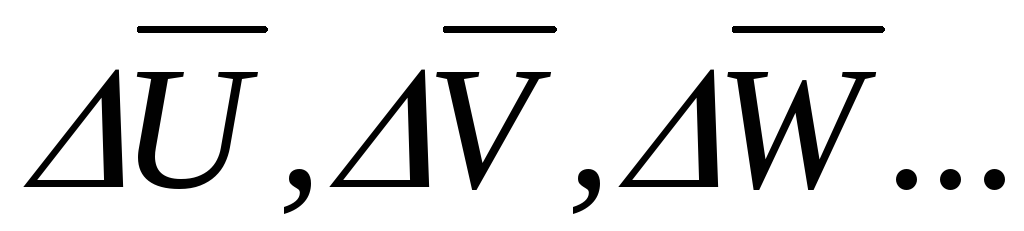по заданной доверительной вероятности и объему выборки для каждой величины по методике, оценке случайной погрешности прямых измерений приведенной в 4. При этом вероятность 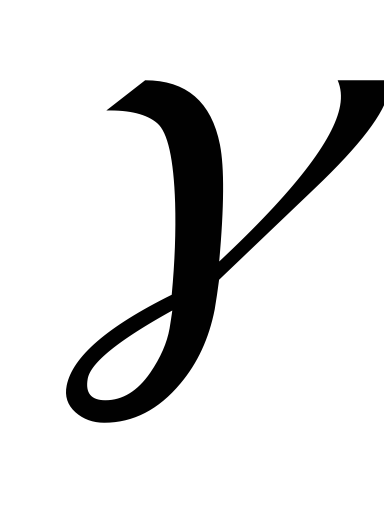должна быть одинаковой для всех 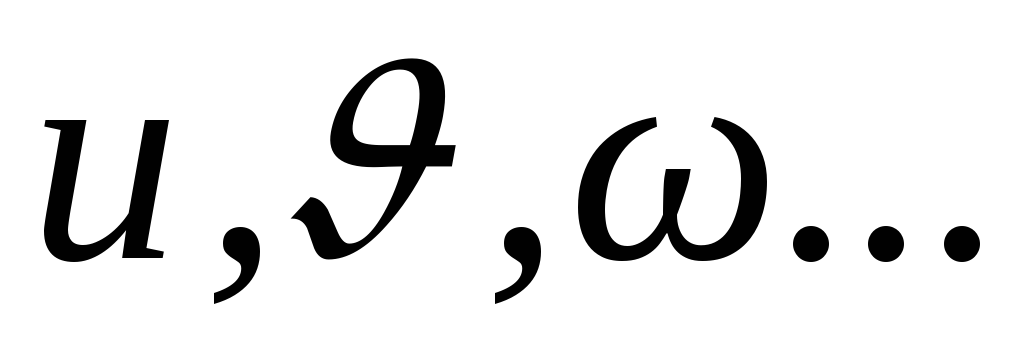, а объем выборки может быть для них различным.

2. находится среднее значение результата косвенных измерений по формуле (23).

3. находится абсолютная погрешность косвенного измерения по формуле (24).

4. записывается результат измерения:

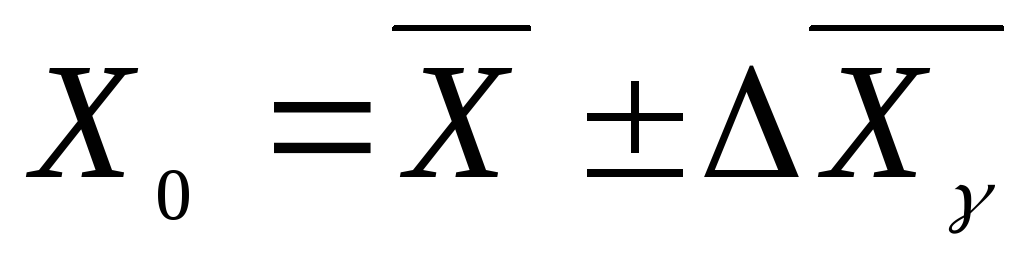
Правила приближенных вычислений, записи погрешностей и результатов измерения

1. Экспериментальные результаты измерения являются приближенными числами, поэтому при их записи следует указывать величину погрешности. Как было видно выше, вычисляемая практически среднеквадратическая и абсолютная погрешности характеризуют реальные погрешности приближенно, поэтому указывать их величину с большой точностью бессмысленно. Значение погрешности нужно округлять, оставив одну или две значащие цифры. В частности, если это цифры 1 или 2, то следует обязательно привести и вторую значащую цифру.

Например, нужно писать

, а не 0,0553

или , а не2,36.

2. Число значащих цифр результата 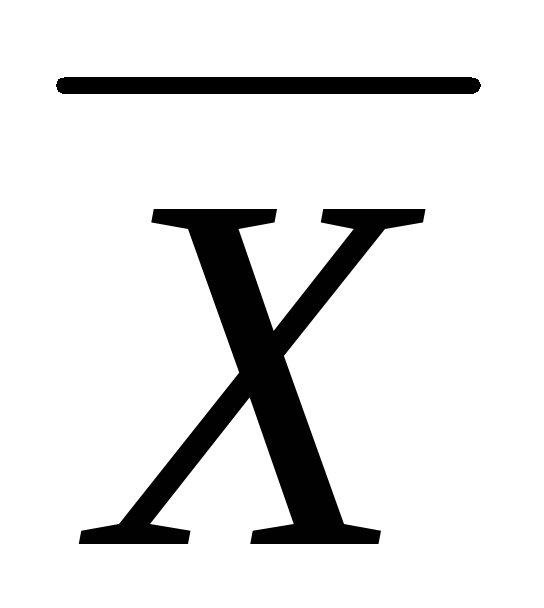также ограничено и определяется порядком величины погрешности. Если, например, величина погрешности составляет сотые доли, т.е. если мы не ручаемся за правильность сотых долей, нет смысла сохранять тысячные доли и результат следует округлить до сотых долей. В общем случае, запись окончательного значения измеряемой величины 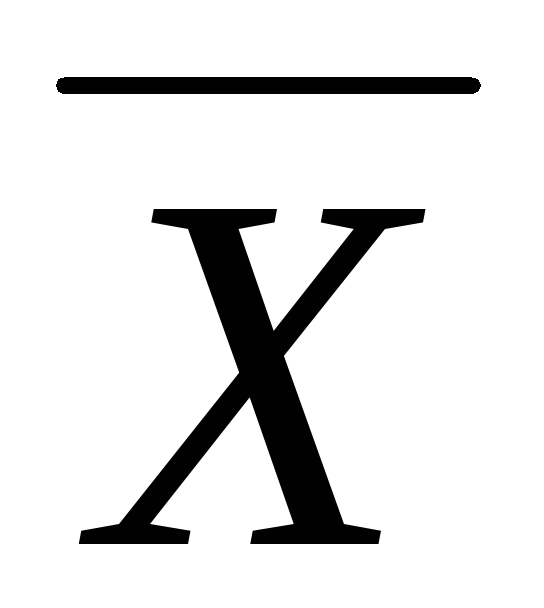и ее погрешность 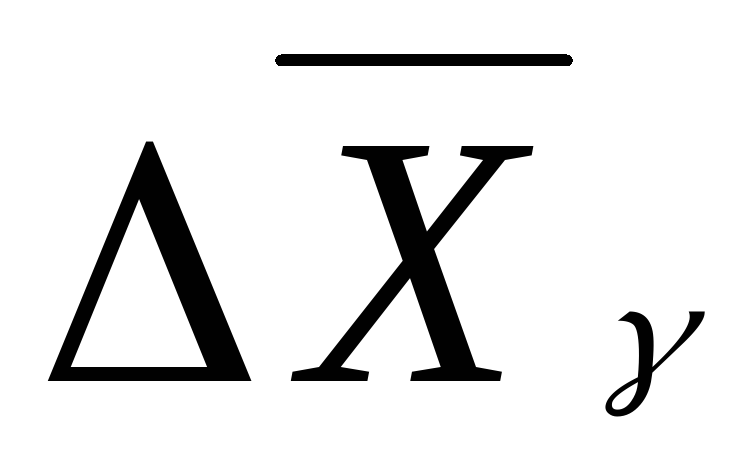нужно приводить с одинаковым числом десятичных знаков.

Например, надо писать:

U = (15,3 ± 0,3), а не U = (15,33 ± 0,3)

3. Абсолютную погрешность всегда выражают в тех же единицах, что и саму измеряемую величину, например:

l= (1,572 0,004) м,

см/с

но не

l= 1,572 4 м,

см/с

Последняя запись совершенно неприемлема, т. к. не позволяет сразу увидеть, какая цифра результата является ненадежной.

4. При проведении расчетов по результатам измерений необходимо помнить, что мы имеем дело с приближенными численными значениями, поэтому необходимо знать основные правила выполнения приближенных вычислений. Напомним их:

а) при округлении следует прибавить единицу в соседний старший разряд записи числа, если отбрасывается цифра младшего разряда 5 или больше, и просто отбросить ее, если она меньше 5. например, 4,08 округляя до двух значащих цифр получим: 4,1; 4,03 ≈ 4,0, а не просто 4, т.к. запись 4, 0 означает округление до двух значащих цифр, а просто 4 – только одной.

б) при сложении и вычитании приближенных чисел следует сохранять в окончательном результате и в слагаемых не больше знаков после запятой, чем их имеется в наименее достоверном числе.

Пример. При сложении чисел:

4,462 + 2,38 + 1,17273 +1,0262 = 9,04093

определив наименее достоверное число (2,28) следует слагаемые и сумму округлить до сотых долей, т.е.:

4,46 + 2,38 + 1,17 +1,03 = 9,04;

в) при умножении и делении исходные данные округляются, сохраняя лишь одну лишнюю значащую цифру по сравнению с наименее достоверн6ым числом, результат округляется до числа значащих цифр в наименее достоверном числе.